在之前的几篇文章中,我们介绍了基于价值Value的强化学习算法Deep Q Network。有关DQN算法以及各种改进算法的原理和实现,可以参考之前的文章:
实战深度强化学习DQN-理论和实践:https://www.jianshu.com/p/10930c371cac
DQN三大改进(一)-Double DQN:https://www.jianshu.com/p/fae51b5fe000
DQN三大改进(二)-Prioritised replay:https://www.jianshu.com/p/db14fdc67d2c
DQN三大改进(三)-Dueling Network:https://www.jianshu.com/p/b421c85796a2
基于值的强化学习算法的基本思想是根据当前的状态,计算采取每个动作的价值,然后根据价值贪心的选择动作。如果我们省略中间的步骤,即直接根据当前的状态来选择动作。基于这种思想我们就引出了强化学习中另一类很重要的算法,即策略梯度(Policy Gradient)。之前我们已经介绍过策略梯度的基本思想和实现了,大家可以有选择的进行预习和复习:
深度强化学习-Policy Gradient基本实现:https://www.jianshu.com/p/2ccbab48414b
当基于值的强化学习方法和基于策略梯度的强化学习方法相结合,我们就产生了Actor-Critic方法,关于这个方法的介绍,可以参考文章:
深度强化学习-Actor-Critic算法原理和实现:https://www.jianshu.com/p/25c09ae3d206
但是对于Actor-Critic算法来说,模型涉及到了两个神经网络, 而且每次都是在连续状态中更新参数, 每次参数更新前后都存在相关性, 即模型的训练数据不再是独立同分布,这导致神经网络只能片面的看待问题, 甚至导致神经网络学不到东西。想想我们之前介绍的DQN是如何解决的这个问题的?就是建立了两个网络,一个target网络,一个eval网络,同时使用了经验回放机制!那么如果在Actor-Critic网络结构中加入这两个机制,就得到了一种新的强化学习模型:Deep Deterministic Policy Gradient,简称DDPG!可以说Actor-Critic + DQN = DDPG,今天,我们就来一探DDPG的究竟!
1、DDPG原理
什么是DDPG呢
什么是DDPG呢?前面我们介绍过了,它是Actor-Critic 和 DQN 算法的结合体。
DDPG的全称是Deep Deterministic Policy Gradient。
我们首先来看Deep,正如Q-learning加上一个Deep就变成了DQN一样,这里的Deep即同样使用DQN中的经验池和双网络结构来促进神经网络能够有效学习。
再来看Deterministic,即我们的Actor不再输出每个动作的概率,而是一个具体的动作,这更有助于我们连续动作空间中进行学习。之前不太理解这个连续动作空间是什么意思,既然policy gradient和dqn都是输出每个动作的概率和q值,那么我们为什么还要用policy gradient呢?这个连续动作空间的例子可以举一个么?既然已经诚心诚意的发问了,那么我就班门弄斧回答一下。假如想要通过强化学习得到一个词的32维词向量,哇,这个词向量的动作空间可是无限大的呀,[1,0....0]是一个动作,[0,1...0]是一个动作,如果加上小数,那更是数不过来啦,这时候我们根本不可能去计算每个动作的概率或者q值,我们只能给定状态即一个单词,直接输出一个合适的词向量。类似于这种情况,DDPG就可以大显神威了。
DDPG的网络结构
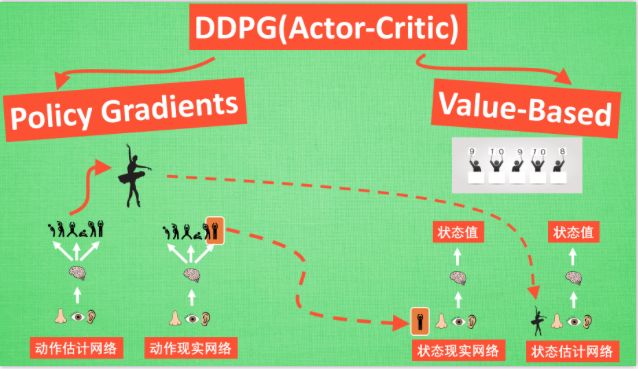
盗用莫烦老师的一张图片来形象的表示DDPG的网络结构,同图片里一样,我们称Actor里面的两个网络分别是动作估计网络和动作现实网络,我们称Critic中的两个网络分别是状态现实网络和状态估计网络:
我们采用了类似DQN的双网络结构,而且Actor和Critic都有target-net和eval-net。我们需要强调一点的事,我们只需要训练动作估计网络和状态估计网络的参数,而动作现实网络和状态现实网络的参数是由前面两个网络每隔一定的时间复制过去的。
我们先来说说Critic这边,Critic这边的学习过程跟DQN类似,我们都知道DQN根据下面的损失函数来进行网络学习,即现实的Q值和估计的Q值的平方损失:
上面式子中Q(S,A)是根据状态估计网络得到的,A是动作估计网络传过来的动作。而前面部分R + gamma * maxQ(S',A')是现实的Q值,这里不一样的是,我们计算现实的Q值,不在使用贪心算法,来选择动作A',而是动作现实网络得到这里的A'。总的来说,Critic的状态估计网络的训练还是基于现实的Q值和估计的Q值的平方损失,估计的Q值根据当前的状态S和动作估计网络输出的动作A输入状态估计网络得到,而现实的Q值根据现实的奖励R,以及将下一时刻的状态S'和动作现实网络得到的动作A' 输入到状态现实网络 而得到的Q值的折现值加和得到(这里运用的是贝尔曼方程)。
我们再来说一下Actor这边,论文中,我们基于下面的式子进行动作估计网络的参数:
这个式子看上去很吓人,但是其实理解起来很简单。假如对同一个状态,我们输出了两个不同的动作a1和a2,从状态估计网络得到了两个反馈的Q值,分别是Q1和Q2,假设Q1>Q2,即采取动作1可以得到更多的奖励,那么Policy gradient的思想是什么呢,就是增加a1的概率,降低a2的概率,也就是说,Actor想要尽可能的得到更大的Q值。所以我们的Actor的损失可以简单的理解为得到的反馈Q值越大损失越小,得到的反馈Q值越小损失越大,因此只要对状态估计网络返回的Q值取个负号就好啦。是不是很简单。
DDPG学习中的小trick
与传统的DQN不同的是,传统的DQN采用的是一种被称为'hard'模式的target-net网络参数更新,即每隔一定的步数就将eval-net中的网络参数赋值过去,而在DDPG中,采用的是一种'soft'模式的target-net网络参数更新,即每一步都对target-net网络中的参数更新一点点,这种参数更新方式经过试验表明可以大大的提高学习的稳定性。'soft'模式到底是如何更新网络的?我们可以通过代码更好的理解。
论文中提到的另一个小trick是对采取的动作增加一定的噪声:
DDPG的完整流程
介绍了这么多,我们也就能顺利理解原文中的DDPG算法的流程:
2、DDPG算法实现
好了,原理介绍的差不多了,我们来看一下代码的实现。本文的代码仍然参考的是莫烦老师的代码。
本文代码的github地址为:https://github.com/princewen/tensorflow_practice/blob/master/Basic-DDPG/DDPG-update.py
定义超参数
我们首先定义网络中的超参数,比如经验池的大小,两个网络的学习率等等:
MAX_EPISODES = 200
MAX_EP_STEPS = 200
LR_A = 0.001 # learning rate for actor
LR_C = 0.002 # learning rate for critic
GAMMA = 0.9 # reward discount
TAU = 0.01 # soft replacement
MEMORY_CAPACITY = 10000
BATCH_SIZE = 32
RENDER = False
ENV_NAME = 'Pendulum-v0'
定义网络输入
我们需要定义的placeholder包括当前的状态S,下一时刻的状态S',以及对应的奖励R,而动作A由Actor得到,因此不需要再定义:
self.S = tf.placeholder(tf.float32, [None, s_dim], 's')
self.S_ = tf.placeholder(tf.float32, [None, s_dim], 's_')
self.R = tf.placeholder(tf.float32, [None, 1], 'r')
构建两个网络
两个网络都是两层全链接的神经网络,Actor输出一个具体的动作,而Critic网络输出一个具体的Q值
def _build_a(self, s, scope, trainable):
with tf.variable_scope(scope):
net = tf.layers.dense(s, 30, activation=tf.nn.relu, name='l1', trainable=trainable)
a = tf.layers.dense(net, self.a_dim, activation=tf.nn.tanh, name='a', trainable=trainable)
return tf.multiply(a, self.a_bound, name='scaled_a')
def _build_c(self, s, a, scope, trainable):
with tf.variable_scope(scope):
n_l1 = 30
w1_s = tf.get_variable('w1_s', [self.s_dim, n_l1], trainable=trainable)
w1_a = tf.get_variable('w1_a', [self.a_dim, n_l1], trainable=trainable)
b1 = tf.get_variable('b1', [1, n_l1], trainable=trainable)
net = tf.nn.relu(tf.matmul(s, w1_s) + tf.matmul(a, w1_a) + b1)
return tf.layers.dense(net, 1, trainable=trainable) # Q(s,a)
soft模式参数更新
可以看到,我们这里进行的是soft模式的参数更新,每次在原来target-net参数的基础上,改变一丢丢,增加一点点eval-net的参数信息。
# networks parameters
self.ae_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='Actor/eval')
self.at_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='Actor/target')
self.ce_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='Critic/eval')
self.ct_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='Critic/target')
# target net replacement
self.soft_replace = [[tf.assign(ta, (1 - TAU) * ta + TAU * ea), tf.assign(tc, (1 - TAU) * tc + TAU * ec)]
for ta, ea, tc, ec in zip(self.at_params, self.ae_params, self.ct_params, self.ce_params)]
定义两个网络的损失
关于两个网络的损失,我们之前已经详细介绍过了,这里只是对刚才思路的一个代码实现。
q_target = self.R + GAMMA * q_
# in the feed_dic for the td_error, the self.a should change to actions in memory
td_error = tf.losses.mean_squared_error(labels=q_target, predictions=q)
self.ctrain = tf.train.AdamOptimizer(LR_C).minimize(td_error, var_list=self.ce_params)
a_loss = - tf.reduce_mean(q) # maximize the q
self.atrain = tf.train.AdamOptimizer(LR_A).minimize(a_loss, var_list=self.ae_params)
学习
我们首先要从经验池中取出一个batch的数据,然后训练我们的Actor和Critic
def learn(self):
# soft target replacement
self.sess.run(self.soft_replace)
indices = np.random.choice(MEMORY_CAPACITY, size=BATCH_SIZE)
bt = self.memory[indices, :]
bs = bt[:, :self.s_dim]
ba = bt[:, self.s_dim: self.s_dim + self.a_dim]
br = bt[:, -self.s_dim - 1: -self.s_dim]
bs_ = bt[:, -self.s_dim:]
self.sess.run(self.atrain, {self.S: bs})
self.sess.run(self.ctrain, {self.S: bs, self.a: ba, self.R: br, self.S_: bs_})
存储经验
def store_transition(self, s, a, r, s_):
transition = np.hstack((s, a, [r], s_))
index = self.pointer % MEMORY_CAPACITY # replace the old memory with new memory
self.memory[index, :] = transition
self.pointer += 1
好啦,我们这里就简单介绍一下代码中的核心部分,其余的代码大家可以参照github进行学习,祝大家清明节快乐,玩得开心,学得开心!
参考文献:
1、https://morvanzhou.github.io/tutorials/machine-learning/reinforcement-learning/6-2-A-DDPG/
2、论文:https://arxiv.org/abs/1509.02971