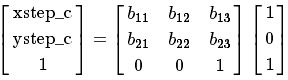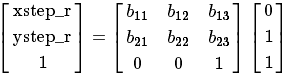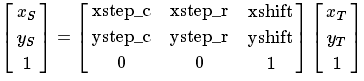造轮子之仿射变换

有人说，我们不应该再造轮子；也有人说，学习怎么造轮子可以带来更深的理解。我说，用轮子有用轮子的乐趣，造轮子有造轮子的乐趣。总之，开心就好。

仿射变换，可能是图像处理中最为基本的变换之一了吧。OpenCV中就有现成的函数，大可以一调了之。然而，如果不能使用OpenCV呢？比如，在DSP上实现。有人会说，TI的DSP直接有一个医学图像库可以调用仿射变换啊。好吧，我被打败了，但TI的医学图像库的仿射变换有一篇文档。那篇文档写得实在是太感人肺腑了，难道我们不该顺便学习一下吗？所以有了这篇文章（其实大多数就是翻译一下啦，不用那么认真。直接看原文吧：））

简介

图像中要使用仿射变换的目的其实就是为了把一个本来已经偏了的东西放正。比如，我之前做的身份证扫描的项目。身份证通过CIS的扫描，变成了一个背景是黑色，前景当然就是身份证的东西了。（透露这么多已经很危险了，就不放图了）可以想象一下，身份证不一定就很正吧，会有些许的倾斜。那问题来了，客户想要的是标标准准的正置着的裁好边的身份证图像。我该怎么做呢？很简单，就是分成两个步骤：

找到身份证的四个顶点的坐标。
利用仿射变换对这四个顶点坐标进行仿射变换。（其实只要三个顶点坐标就OK了。）

举这么个例子，想象力比较丰富的可能就知道仿射变换是要干什么了。仿射变换其实就是图像变换的一列组合，包括：旋转(rotating)、移位(shifting)、缩放(scaling)、切变(shearing)。

图像的变换究竟是怎么变换的呢？事实上，图像的变换其实就是坐标点位置的变换。正变换是这样：知道了原图，知道了变换方式，我们就可以推测出目标图像是哪样。但其实我们使用的往往是逆变换。也就是：我们首先对目标图像有一个大小的期望(分辨率为$W\times H$)，那么每一个像素该填什么值呢？就可以通过逆变换，找到其在原图像上的对应位置。此时，看看原图上的周围像素点是多少，就可以用双线性插值等算法计算出目标图像上该点的像素值了。

基本操作

我们可以写出下面的式子来表示仿射坐标变换的通式：

![][matrix]
[matrix]: http://latex.codecogs.com/svg.latex?p_T=A\cdot{p_S}

其中，

![][00]
[00]: http://latex.codecogs.com/svg.latex?p_S=\left[\begin{array}{c}x_S\y_S\1\\end{array}\right]

![][01]
[01]: http://latex.codecogs.com/svg.latex?p_T=\left[\begin{array}{c}x_T\y_T\1\\end{array}\right]

分别是原点位置和目标点位置。

![][02]
[02]: http://latex.codecogs.com/svg.latex?A=\left[\begin{array}{ccc}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\0&0&1\\end{array}\right]$$

是变换矩阵。这个矩阵可以拆分为如下几个矩阵：

平移矩阵：

![][03]
[03]: http://latex.codecogs.com/svg.latex?A_T=\left[\begin{array}{ccc}1&0&d_x\0&1&d_y\0&0&1\\end{array}\right]

这个平移矩阵的作用就是将图像平移。只要代入原式，就可以看到，

对图像放缩的变换矩阵如下：

![][06]
[06]: http://latex.codecogs.com/svg.latex?A_S=\left[\begin{array}{ccc}\beta_x&0&0\0&\beta_y&0\0&0&1\\end{array}\right]

对图像旋转的变换矩阵如下：

![][07]
[07]: http://latex.codecogs.com/svg.latex?A_R=\left[\begin{array}{ccc}\cos\theta&-\sin\theta&0\\sin\theta&\cos\theta&0\0&0&1\\end{array}\right]

切变也是一种线性变换：

![][08]
[08]: http://latex.codecogs.com/svg.latex?A_Q=\left[\begin{array}{ccc}1&s_x&0\s_y&1&0\0&0&1\\end{array}\right]

其中，s_x和s_y分别是x方向和y方向的切变系数。

原图

沿x方向切变

旋转

综合:仿射变换

算法细节

一般地，我们会去查看目标上的点在原图像上的位置，并用原图像上对应点的像素值插值后得到目标图像上该点的像素值。通过目标点的位置来计算原点的位置使用的是逆变换：

![][09]
[09]: http://latex.codecogs.com/svg.latex?p_S=A^{-1}\cdot{p_T}

![][10]
[10]: http://latex.codecogs.com/svg.latex?A^{-1}=\left[\begin{array}{ccc}b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\0&0&1\\end{array}\right]

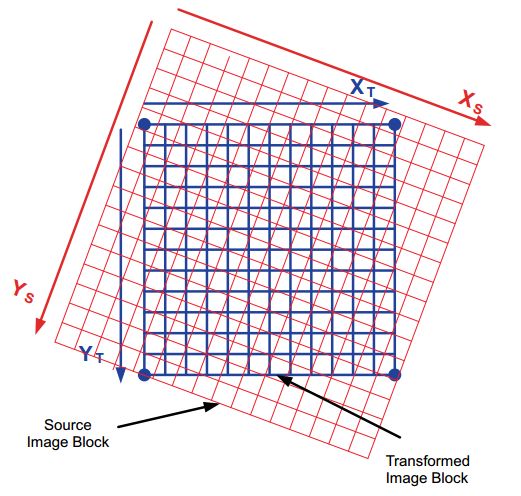
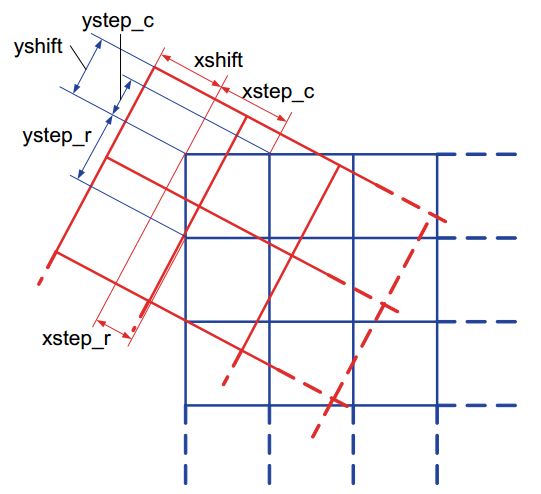
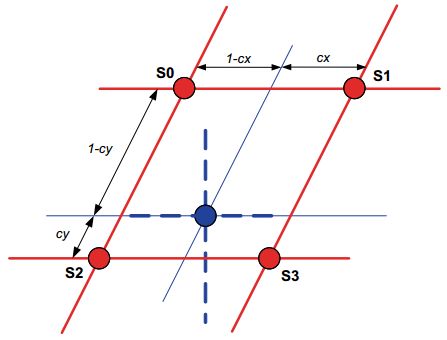
在下图中，蓝色格子表示目标图像，红色格子表示原图像。

目标图像的(0,0)点对应的是原图像的(xshift,yshift)点。从而：

![][11]
[11]: http://latex.codecogs.com/svg.latex?\left[\begin{array}{c}\text{xshift}\\text{yshift}\1\\end{array}\right]=\left[\begin{array}{ccc}b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\0&0&1\\end{array}\right]\left[\begin{array}{c}0\0\1\\end{array}\right]

因此，

![][12]
[12]: http://latex.codecogs.com/svg.latex?b_{13}=xshift,b_{23}=yshift

令[xstep_c,ystep_c]为目标图像移动一列后，原图像的坐标发生的相应的变化。则：