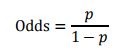申请评分卡对于从事信贷风控行业的人来说肯定不陌生,甚至每天都会应用到。申请评分,即对申请客户打分,对于业务专家来说可以是基于经验对客户资质进行评估,最终决定是否给予通过申请,首先基于经验的评估很难量化,可能还受各种主观因素的影响导致评估标准频繁波动,而基于数据的评估是直接以分数的形式来展现,更容易进行比较,且在建立好模型之后,这套评分标准就已经确定,除非重新构建模型,稳定性更胜一筹。这篇文章主要介绍自己的一些理解以及建立评分卡的过程,第一次尝试建模,如有错误的地方,请指出。
申请评分卡
- 评分卡中的一种,其他还有行为评分卡、催收评分卡等
- 原理是基于客户在过去某个时间点截止到本次贷款或信用卡申请时的各项数据,预测其未来某一段时间内的违约概率,而评分则是以分数的形式来体现这个违约概率,即违约概率越高,对应的评分越低
- 过去某个时间点截止到本次申请即观察期,未来某一段时间即表现期
Logistic回归
- 二分类问题中常用的一种算法,具体内容:机器学习算法系列(一):Logistic回归
本次建模流程目录
一、数据获取与目标变量定义
二、探索性数据分析
三、数据预处理
四、特征工程
五、建立模型
六、模型评估
七、建立评分卡
八、拒绝推论
一、数据获取与目标变量定义
- 导入需要用到的python库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from datetime import datetime
from mpl_toolkits.mplot3d import Axes3D
import woe
import woe.feature_process as fp
import woe.eval as eva
from statsmodels.stats.outliers_influence import variance_inflation_factor
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegressionCV
from sklearn.metrics import roc_curve,auc
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
- 数据获取:取自美国一家P2P平台Lending Club的官网,选取2017年三季度-2018年二季度的放贷数据,数据更新至2019年5月
data17Q3=pd.read_csv('C:\\Users\\honglihui\\Desktop\\LendingClubLoanData-UpdateTime201905\\LoanStats_2017Q3.csv',low_memory=False,header=1)
data17Q4=pd.read_csv('C:\\Users\\honglihui\\Desktop\\LendingClubLoanData-UpdateTime201905\\LoanStats_2017Q4.csv',low_memory=False,header=1)
data18Q1=pd.read_csv('C:\\Users\\honglihui\\Desktop\\LendingClubLoanData-UpdateTime201905\\LoanStats_2018Q1.csv',low_memory=False,header=1)
data18Q2=pd.read_csv('C:\\Users\\honglihui\\Desktop\\LendingClubLoanData-UpdateTime201905\\LoanStats_2018Q2.csv',low_memory=False,header=1)
data=pd.concat([data17Q3,data17Q4,data18Q1,data18Q2],ignore_index=True)#总数据集
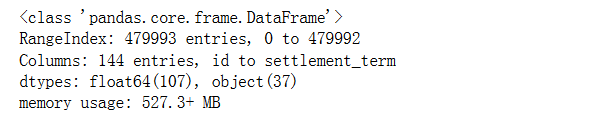
data.info()
<共48万条数据,144个变量,其中float64类变量107个,object类变量37个>
- 目标变量定义:
建立模型预测客户在未来一段时间内是否会违约,那必然需要先定义违约,逾期多长时间算违约,不同业务标准不同。与数据集中还款表现loan_status字段相关,作为目标变量,剩下的字段则作为解释变量 - 还款状态数据分布:
data['loan_status'].groupby(data.loan_status).count()
- 客户的还款表现基本可以反映出这个客户的信用好坏程度,好坏程度可能偏向于主观的判断,在建模之前需要将它量化;
- 好坏客户定义需要根据实际业务来确定,比如可以通过计算滚动率,观察各放款时期中的贷款有多少比例会往更坏的方向发展,并结合表现期(vintage逾期率随账龄增加达到一个稳定值,其对应的账龄长度设定为表现期长度)内的逾期情况来定义好坏客户,例如各放款时间段的平均滚动率:
正常还款-M1为5%
M1-M2为30%
M2-M3为70%
M3-M4为85%
M4-M5为98%
可定义表现期内出现M3一次及以上、M2两次及以上为坏客户,
定义表现期内正常还款、M1不超过一次的为好客户,剩下的定义为不确定,从数据集中剔除;本次数据集缺少历史详细逾期数据,因此这里基于业务直接采取如下定义:其中坏客户标记为1,好客户标记为0,不确定的标记为Undefined:
loan_status_dict={'Charged Off':1,'Default':1,'Late (31-120 days)':1,
'Fully Paid':0,'Current':0,
'In Grace Period':'Undefined','Late (16-30 days)':'Undefined'}
替换原始还款状态为标记值{0,1,Undefined}:
data.loan_status.replace(to_replace=loan_status_dict,inplace=True)
值替换后的贷款状态字段:
data['loan_status'].groupby(data.loan_status).count()
更新数据,只保留{0,1}数据,并修改目标变量名为target:
data=data[data.loan_status.isin([1,0])]
data.rename(columns={'loan_status':'target'},inplace=True)
重置index:
data.reset_index(drop=True,inplace=True)
剩余475404组数据:
data.info()
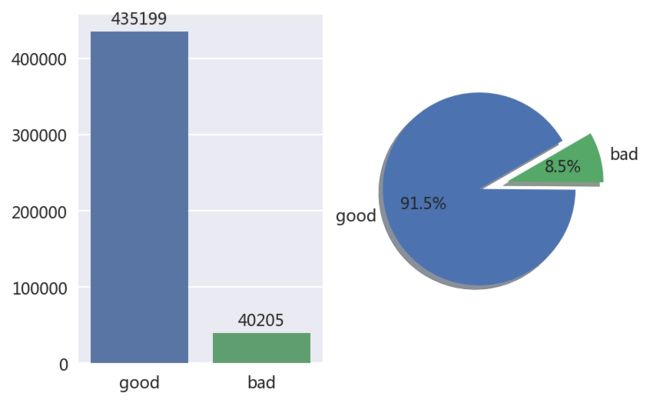
- 好坏客户分布与占比:
sns.set_style('darkgrid')
plt.rcParams['font.sans-serif']='Microsoft YaHei'
plt.rcParams['figure.dpi']=150
plt.subplot(121)
bad=data.target.sum() #正样本量
good=data.shape[0]-bad #负样本量
sns.barplot(x=['good','bad'],y=[good,bad])
plt.text(0,good+10000,good,ha='center',va='baseline',fontsize=10)
plt.text(1,bad+10000,bad,ha='center',va='baseline',fontsize=10)
plt.subplot(122)
bad_ratio=data.target.sum()/data.shape[0]#正样本占比
good_ratio=1-bad#负样本占比
plt.pie([good,bad],labels=['good','bad'],autopct='%1.1f%%',startangle=30,explode=[0,0.3],textprops={'fontsize':10},shadow=True)
plt.axis('equal')
二、探索性数据分析
- 数据基本分布
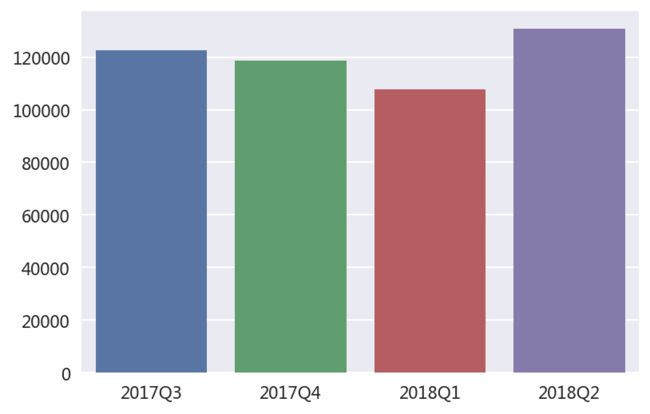
- 各个季度的放款量:
sns.barplot(x=('2017Q3','2017Q4','2018Q1','2018Q2'),
y=[data17Q3.shape[0],data17Q4.shape[0],data18Q1.shape[0],data18Q2.shape[0]])
<各季度放款量基本一致,在12万左右>
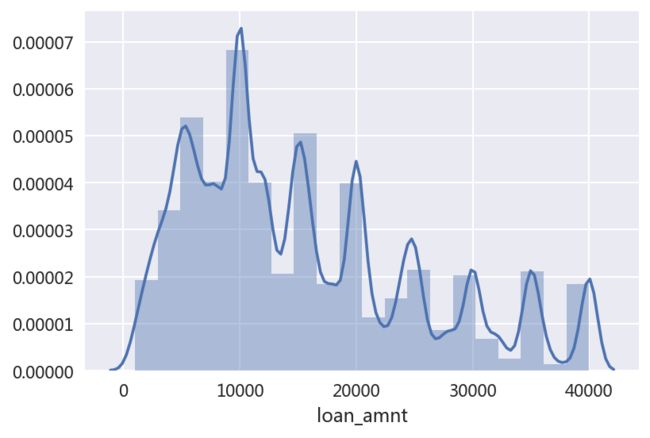
- 贷款金额分布:
draw=data.copy()#用于作图的数据副本
sns.distplot(a=draw.loan_amnt,bins=20)
<申请金额均不超过4万,小额贷款占多数,金额分布主要集中在5000-20000>
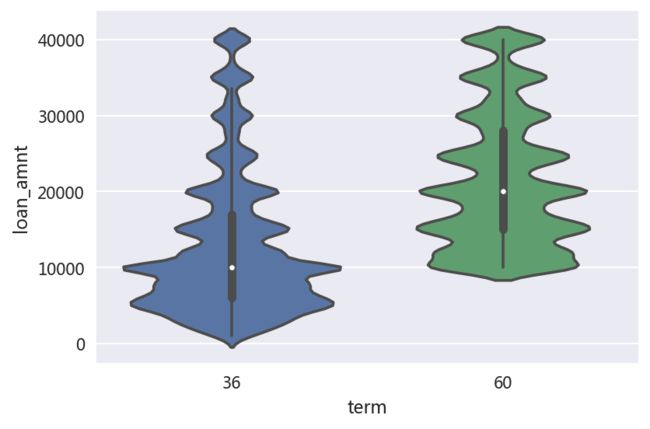
- 借款期限、贷款金额分布:
draw['term']=draw['term'].str.replace('months',' ').str.strip().astype('int')
sns.violinplot(x=draw['term'],y=draw['loan_amnt'])
<期限有36期和60期,36期的金额主要在10000及以下,60期的金额主要在10000以上>
- 借款金额、利率随客户等级的变化:
draw['int_rate']=draw['int_rate'].str.replace('%',' ').str.strip().astype('float')
plt.subplot(211)
sns.violinplot(x=draw['grade'],y=draw['loan_amnt'])
plt.subplot(212)
sns.violinplot(x=draw['grade'],y=draw['int_rate'])
plt.ylabel('int_rate(%)',fontdict={'fontsize':11},labelpad=20)
<借款利率大致随等级的降低而增加,F等级利率分布比较特殊,这可能与它的借款金额有一定关系,主要集中在10000以上,对应的借款期限多为60期,利率也会偏高>
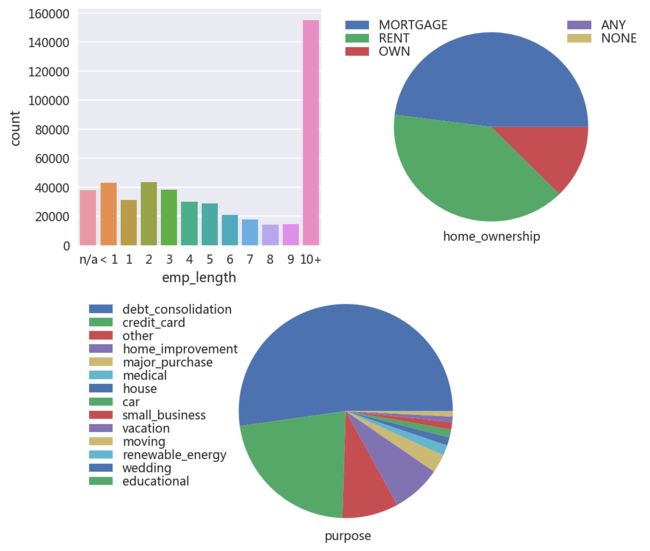
- 工作年限、住房类型、贷款用途分布:
draw['emp_length']=draw.emp_length.str.replace('years',' ').str.strip()
draw['emp_length']=draw.emp_length.str.replace('year',' ').str.strip()
#data['emp_length']=data.emp_length.replace({'10+':'10','< 1':'0','n/a':'-1'}).astype('float64')
plt.figure(figsize=(8,8))
plt.subplot(221)
el=draw.emp_length.groupby(draw.emp_length).count()
sns.barplot(x=el.index,y=el,order=['n/a','< 1','1','2','3','4','5','6','7','8','9','10+'])
plt.ylabel('count')
plt.subplot(222)
ho=draw.home_ownership.groupby(draw.home_ownership).count()
ho_ratio=(ho/draw.shape[0]).sort_values(ascending=False)
plt.pie(ho_ratio)
plt.legend(ho_ratio.index,loc=9,ncol=2,labelspacing=0.05,columnspacing=10)
plt.text(-0.5,-1.2,'home_ownership',fontsize=10)
plt.subplot(212)
pp=draw.purpose.groupby(draw.purpose).count()
pp_ratio=(pp/draw.purpose.shape[0]).sort_values(ascending=False)
plt.pie(pp_ratio)
plt.legend(pp_ratio.index,loc=0,labelspacing=0.05)
plt.text(-0.2,-1.2,'purpose',fontsize=10)
plt.axis('equal')
<客户群体工作年限在10年以上占多数>
<住房类型主要有按揭、租住、自有三种>
<贷款用途主要集中在债务合并、偿还信用卡、其他、房屋装修四种>
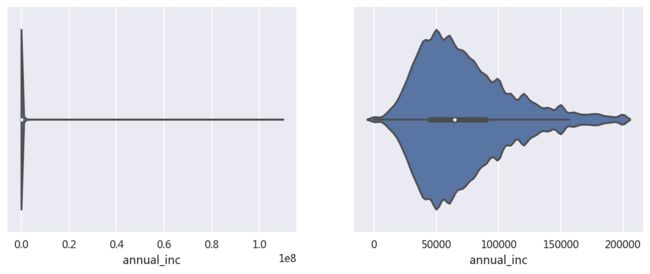
- 年收入分布:
plt.figure(figsize=(11,4))
plt.subplot(121)
sns.violinplot(draw.annual_inc)
plt.subplot(122)
sns.violinplot(draw.annual_inc[draw.annual_inc<=200000])
<左图分析可知群体收入存在较大差异,大部分年收入在20万以下>
<右图是20万及以下的收入分布,可以看出大部分客户的年收入在5万左右,中位值65000>
- 各个因素与还款表现之间的关系
- 贷款金额、借款期限与还款表现:
plt.figure(figsize=(8,8))
plt.subplot(211)
sns.violinplot(x=draw.term,y=draw.loan_amnt,hue=draw.target)
plt.legend(loc=0)
plt.subplot(212)
bad_ratio=draw.target.groupby(draw.term).sum()/draw.target.groupby(draw.term).count()
sns.barplot(x=bad_ratio.index,y=bad_ratio,color='#e6daa6')
plt.subplots_adjust(hspace=0.1)
plt.ylabel('bad_ratio')
<好、坏客户在借款金额分布上没有明显的区分度>
<借款期限越长,越可能出现违约>
- 客户等级与还款表现:
bad_ratio=draw.target.groupby(draw.grade).sum()/draw.target.groupby(draw.grade).count()#坏客户占比
bad_ratio.plot(kind='line')
plt.ylabel('bad_ratio')
<相关性较强,客户等级越低,还款表现越差>
- 工作年限与还款表现:
draw['emp_length']=draw.emp_length.replace({'10+':'10','< 1':'0','n/a':'-1'}).astype('float64')
grouped=draw.target.groupby(draw.emp_length)
bad_ratio=grouped.sum()/grouped.count()
bad_ratio.plot()
plt.xticks(range(-1,11),('n/a','< 1','1','2','3','4','5','6','7','8','9','10+'))
plt.ylabel('bad_ratio')
<工作年限大致可以反映一个客户的还款能力,工作年限越长,还款表现越好>
<工作年限为空值的群体坏客户占比存在明显的偏离,猜测这部分群体在申请时未填写此记录可能是因为没有工作>
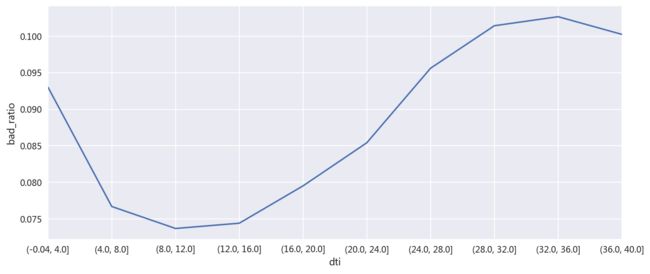
- 负债收入比(dti)与还款表现:
draw.dti.fillna(draw.dti.median(),inplace=True)#缺失值处理
dt=draw[['dti','target']][draw.dti<=40] #dti取值主要集中在40以下,取该部分值来分析
grouped=pd.cut(dt.dti,10)#区间分段
bad_ratio=dt['target'].groupby(grouped).sum()/dt['target'].groupby(grouped).count()#坏客户占比
bad_ratio.plot(figsize=(12,5))
plt.ylabel('bad_ratio')
<以业务的角度分析,dti越高则对应的还款压力越大,违约的概率就越高,趋势图大致是单调递增的,但在这个数据集中并不是这样的分布,可以看出dti在4-16之间的客户群还款表现最好,而dit<4的群体中坏客户占比明显偏高>
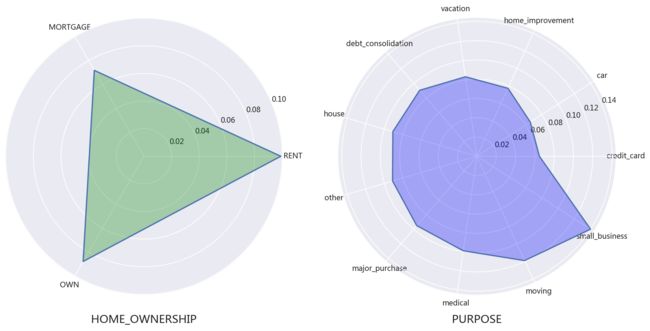
- 住房类型、借款用途与还款表现:
bad_ratio=draw.target.groupby(draw.home_ownership).sum()
/draw.target.groupby(draw.home_ownership).count()
bad_ratio=bad_ratio[['RENT','MORTGAGE','OWN']] #只选取数据量较多的类别
plt.figure(figsize=(15,10))#设置画布大小
point=np.linspace(0, 2*np.pi,bad_ratio.shape[0],endpoint=False)
values=bad_ratio.values
point=np.concatenate((point,[point[0]]))
values=np.concatenate((values,[values[0]]))
plt.subplot(121,polar=True)#图1
plt.plot(point,values)
plt.thetagrids(point*180/np.pi,bad_ratio.index)
plt.fill(point,values,'g',alpha=0.3)
plt.xlabel('HOME_OWNERSHIP',labelpad=27,fontdict={'fontsize':15})
#-------------------------------------------------------------------------------------------------
bad_ratio=draw.target.groupby(draw.purpose).sum()
/draw.target.groupby(draw.purpose).count()
bad_ratio.sort_values(inplace=True)
index=~bad_ratio.index.isin(['wedding','educational','renewable_energy'])#这三个数据量较少,不考虑在内
bad_ratio=bad_ratio[index]
point=np.linspace(0, 2*np.pi,bad_ratio.shape[0],endpoint=False)
values=bad_ratio.values
point=np.concatenate((point,[point[0]]))
values=np.concatenate((values,[values[0]]))
plt.subplot(122,polar=True)#图2
plt.plot(point,values)
plt.thetagrids(point*180/np.pi,bad_ratio.index)
plt.fill(point,values,'b',alpha=0.3)
plt.xlabel('PURPOSE',labelpad=10,fontdict={'fontsize':15})
<房产类型为按揭的客户群还款表现好于其他>
<借款用于偿还信用卡的客户群体还款好于其他,而借款用途为经商的风险最高>
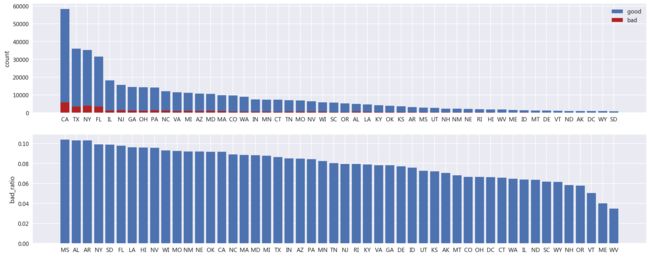
- 区域成交量分布与还款表现:
bad=draw.target.groupby(draw.addr_state).sum()#按地区分组的坏客户
good=draw.target.groupby(draw.addr_state).count()-bad#按地区分组的好客户
bad_ratio=bad/(bad+good)#各地区坏客户占比
good.sort_values(ascending=False,inplace=True)
bad_ratio.sort_values(ascending=False,inplace=True)
plt.figure(figsize=(20,8))
plt.subplot(211)#图1
plt.bar(good.index,good)
plt.bar(bad.index,bad,color='#B22222')
plt.legend(['good','bad'])
plt.ylabel('count')
plt.subplot(212)#图2
plt.bar(bad_ratio.index,bad_ratio)
plt.ylabel('bad_ratio')
<成交的客户主要来自CA(加利福尼亚州)、TX(得克萨斯州)、NY(纽约州)、FL(佛罗里达州),占30%以上>
<还款表现最差的三个州是MS(密西西比州)、AL(亚拉巴马州)、AR(阿肯色州)>
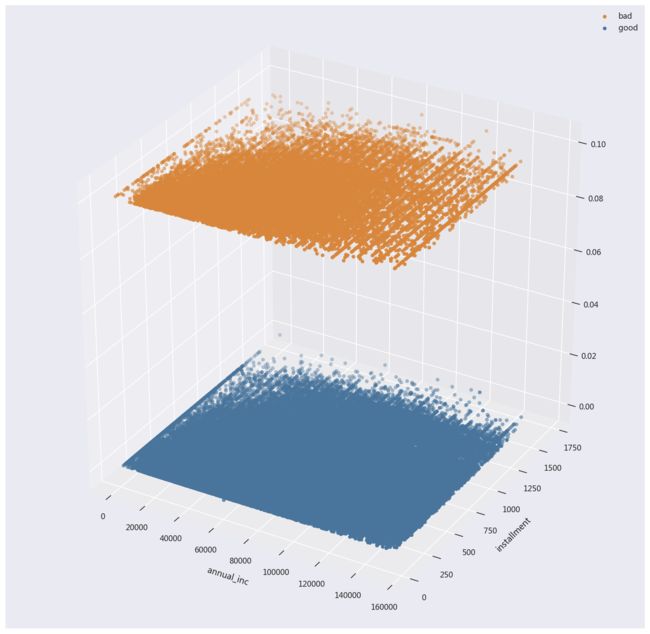
- 好坏客户在收入、月供这两个维度上的分布情况:
fig=plt.figure(figsize=(15,15))
ax=fig.add_subplot(111,projection='3d')
draw=draw[draw.annual_inc<'155000']#选取收入分布比较集中的部分
draw_bad=draw[draw.target==1]#选取坏客户
draw_good=draw[draw.target==0]#选取好客户
ax.scatter(draw_bad.annual_inc,draw_bad.installment,c='#d8863b',zs=0.1)
ax.scatter(draw_good.annual_inc,draw_good.installment,c='#49759c')
ax.set_xlabel('annual_inc',labelpad=13)
ax.set_ylabel('installment',labelpad=13)
ax.legend(['bad','good'])
三、数据预处理
- 变量预处理
- 变量初筛与特征衍生:
(1)计算每个变量缺失率
num_of_null=(data.isnull().sum()/data.shape[0]).sort_values(ascending=False)
num_of_null.plot(kind='bar',figsize=(50,15),fontsize=23)
缺失达90%的变量包含的信息太少,直接删除,缺失20%-90%之间的待定,可能存在一些比较有用的信息,这里选择做进一步分析,缺失20%以下的进行填充
删除缺失率90%以上的变量:
thresh=data.shape[0]*0.1
data.dropna(thresh=thresh,axis=1,inplace=True)
缺失20%-90%之间的变量:
num_of_null.loc[(num_of_null>0.2) & (num_of_null<=0.9)]
通过分析可知缺失率为86%以上的变量相似,都是关于共同借款人的信息,由于原表中已有变量application_type用于区分单人申请还是共同申请,所以与共同申请人有关的变量全部删除,只保留application_type用于区分是否有共同申请人:
data.drop(['sec_app_revol_util','verification_status_joint','revol_bal_joint',
'annual_inc_joint','sec_app_earliest_cr_line','sec_app_inq_last_6mths',
'sec_app_mort_acc','sec_app_open_acc','sec_app_open_act_il',
'sec_app_num_rev_accts','sec_app_chargeoff_within_12_mths',
'sec_app_collections_12_mths_ex_med',
'dti_joint'],axis=1,inplace=True)
剩下的mths_*变量均表示自客户在银行、公开记录、借贷平台的最近一次违约以来的月份数,比如mths_since_last_major_derog表示自最近一次出现90+以来的月份数,考虑到这些变量与目标变量之间存在一定关联,因此先保留,后续将缺失值归为一类
最后next_pymnt_d属于贷后变量,申请阶段是没有的,不应存在于申请评分卡中,其他的贷后变量也一并删除:
data.drop(['next_pymnt_d','last_pymnt_amnt','last_pymnt_d','pymnt_plan','last_credit_pull_d',
'collection_recovery_fee','recoveries','debt_settlement_flag','hardship_flag',
'total_rec_late_fee','total_rec_int','total_rec_prncp','total_pymnt_inv','total_pymnt',
'out_prncp_inv','out_prncp','initial_list_status'],axis=1,inplace=True)
(2)变量取值分布分析:若数据集在某一个属性上取值都相同或接近,那区分度就越小
计算出各个变量中取同值的占比情况:
column=[]
samerate=[]
columns=data.columns
for col in columns:
grouped_max=data[col].groupby(data[col]).count().max()
grouped_sum=data[col].groupby(data[col]).count().sum()
same_rate=grouped_max/grouped_sum
column.append(col)
samerate.append(same_rate)
sr=pd.Series(samerate,index=column)
sr.sort_values(ascending=False)
可见变量policy_code所有取值都一样,无区分度,应剔除,考虑到后面会统一用IV值进行变量选择,所以这里剩下的暂时先不处理:
data.drop('policy_code',axis=1,inplace=True)#剔除变量policy_code
(3)基于业务理解对变量进行简单剔除:
funded_amnt:该时间点筹集的总贷款金额,与loan_amnt完全一致
funded_amnt_inv:该时间点筹集款中来自于投资人的金额,与loan_amnt相差不大
sub_grade:grade的细分等级
title:贷款用途,与purpose大致相同
zip_code:邮政编码
emp_title:借款人自己填写的工作职位且分类杂乱,有效性不高
data.drop(['funded_amnt','funded_amnt_inv','sub_grade','title','zip_code','emp_title'],axis=1,inplace=True)
(4)特征衍生:
earliest_cr_line:拥有信用额度的最早日期
issue_d:放款日期
构造衍生变量1:客户在申请时已拥有的信用历史月数mths_since_earliest_cr_line=issue_d-earliest_cr_line,并删除原始变量;
installment:贷款月供
annual_inc:年收入
构造衍生变量2:贷款月供与月收入比installment_income_ratio,与原始数据集中变量dti不同的是负债项只考虑本次贷款负债;
#构造衍生变量1:
mths_since_earliest_cr_line=[]
datediff=pd.to_datetime(data.issue_d)-pd.to_datetime(data.earliest_cr_line)
for i in datediff:
mthsdiff=round(i.days/30)
mths_since_earliest_cr_line.append(mthsdiff)
data.insert(10,column='mths_since_earliest_cr_line',value=mths_since_earliest_cr_line)#插入新增变量1数据
data['mths_since_earliest_cr_line']=data['mths_since_earliest_cr_line'].astype('float64')
data.drop(['issue_d','earliest_cr_line'],axis=1,inplace=True)
#构造衍生变量2:
monthly_income=data.annual_inc/12
installment_income_ratio=data.installment/monthly_income
installment_income_ratio=round(installment_income_ratio,2)
data.insert(8,'installment_income_ratio',installment_income_ratio)#插入新增变量2数据
data['installment_income_ratio']=data['installment_income_ratio'].astype('float64')
剩余变量:
data.info()
<经过一系列特征初筛和特征衍生,变量已经从144个降低至82个>
(5)变量分类:为了便于后续的自动分箱操作,这里先对数据做一些处理和分类
data['int_rate']=data.int_rate.str.replace('%',' ').str.strip().astype('float64')
data['revol_util']=data.revol_util.str.replace('%',' ').str.strip().astype('float64')
data['term']=data.term.str.replace('months',' ').str.strip()
data['emp_length']=data.emp_length.str.replace('years',' ').str.strip()
data['emp_length']=data.emp_length.str.replace('year',' ').str.strip()
data['emp_length']=data.emp_length.replace({'10+':10,'< 1':0,'n/a':-1}).astype('float64')
discrete_col=data.columns[data.dtypes=='object'].drop('target')#离散型变量,不包含目标变量target
continuous_col=data.columns[data.dtypes=='float64']#连续型变量
- 缺失值处理
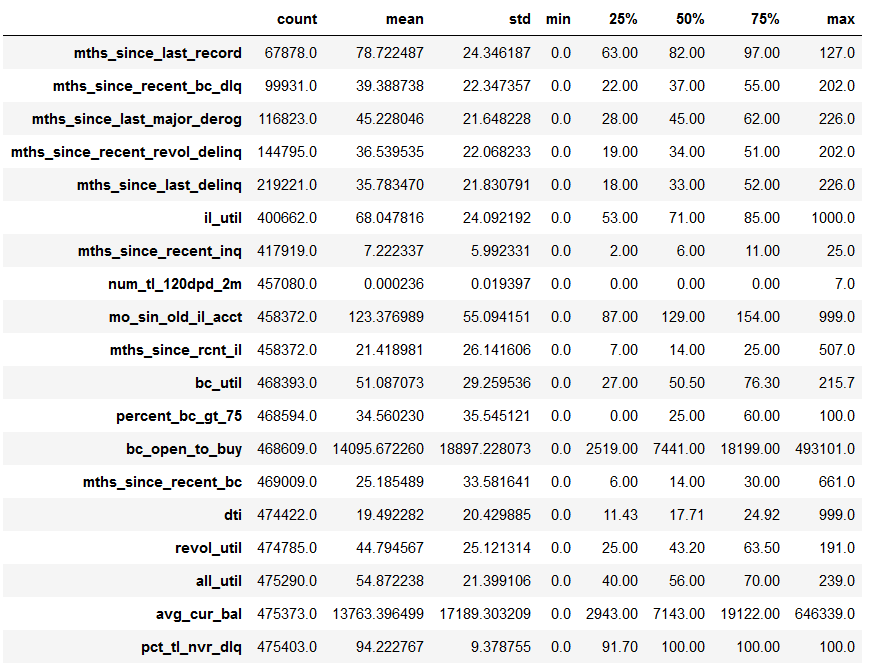
各变量缺失情况:
num_of_null_new=(data.isnull().sum()/data.shape[0]).sort_values(ascending=False)
has_null=num_of_null_new[num_of_null_new>0]
has_null
含缺失值的变量数据概况:可以大致了解各个含缺失值的变量分布情况
data[has_null.index].describe().T
- 缺失率达50%以上的变量:mths_*
<由于这部分缺失值占多数,不能简单地以均值、中位数、众数等方法填充。基于字段含义与业务将这些变量统一理解为:自上一次不良记录或查询以来的月份数,月份数与客户申请贷款时的资质应大致呈现正相关关系,在这些变量上出现缺失很可能代表客户从未出现过该类不良记录或查询记录,后续分箱中positive_rate呈现单调性也验证了自己的猜测。这里将缺失值单独归为一类,且取值与其他群体要有明显的区分>
data['mths_since_recent_inq'].fillna(value=99,inplace=True)
data['mths_since_last_delinq'].fillna(value=999,inplace=True)
data['mths_since_last_record'].fillna(value=999,inplace=True)
data['mths_since_recent_bc_dlq'].fillna(value=999,inplace=True)
data['mths_since_last_major_derog'].fillna(value=999,inplace=True)
data['mths_since_recent_revol_delinq'].fillna(value=999,inplace=True)
- 剩下部分变量缺失不多,选择以中位数填充:
missing=['il_util','num_tl_120dpd_2m','mo_sin_old_il_acct','mths_since_rcnt_il',
'bc_util','percent_bc_gt_75','bc_open_to_buy','mths_since_recent_bc','dti',
'revol_util','all_util','avg_cur_bal','pct_tl_nvr_dlq']
data[missing]=data[missing].apply(lambda x:x.fillna(x.median()))
四、特征工程
- 数据分箱
- 数据分箱是指将连续变量按某一分箱方法进行数据离散化;
- 方法有无监督分箱和有监督分箱,无监督分箱比如等频、等距分箱;有监督分箱比如卡方分箱、决策树算法分箱、基于IV值分箱等,我这里采用的是基于IV值最大化的分箱方法;
- 基本原理:计算单个连续型变量的初始IV值iv0,将单个连续型变量的取值按从小到大排列,等频标记n个划分点,遍历每个划分点i,并计算以每个点划分时的IV值iv(i),取最大IV值max(iv(i)),与iv0+alpha比较,其中alpha是预设值,默认取0.01,若max(iv(i))>iv0+alpha,则进行划分,将数据一分为二,并分别计算两部分初始IV值iv0(L)、iv0(R),分别重复之前的步骤,一直划分到均不满足max(iv(i))>iv0+alpha为止,这个基于两个前提:一是划分后每个区段中的样本量不能太少,可设置阈值;二是划分后每个区段必须同时包含正负样本。
<<关于IV和下文中的WOE:数据挖掘模型中的IV和WOE详解
- 连续型变量自动分箱:
continuous=[]
for col in continuous_col:
con=fp.proc_woe_continuous(df=data,
var=col,#变量名
global_bt=data.target.sum(),#正样本总量
global_gt=data.shape[0]-data.target.sum(),#负样本总量
min_sample=0.05*data.shape[0],#单个区间最小样本量阈值
alpha=0.01)
continuous.append(con)
- 离散型变量自动分箱:
discrete=[]
for col in discrete_col:
dis=fp.proc_woe_discrete(df=data,
var=col,#变量名
global_bt=data.target.sum(),#正样本总量
global_gt=data.shape[0]-data.target.sum(),#负样本总量
min_sample=0.05*data.shape[0])#单个区间最小样本量阈值
discrete.append(dis)
- 分箱结果输出:导出至Excel
df_continuous=eva.eval_feature_detail(Info_Value_list=continuous)#连续型变量分箱结果
df_discrete=eva.eval_feature_detail(Info_Value_list=discrete)#离散型变量分箱结果
bined=pd.concat([df_continuous,df_discrete])#合并
bined.to_csv('C:\\Users\\honglihui\\Desktop\\LendingClubLoanData-UpdateTime201905\\bined.csv',index=False)
-
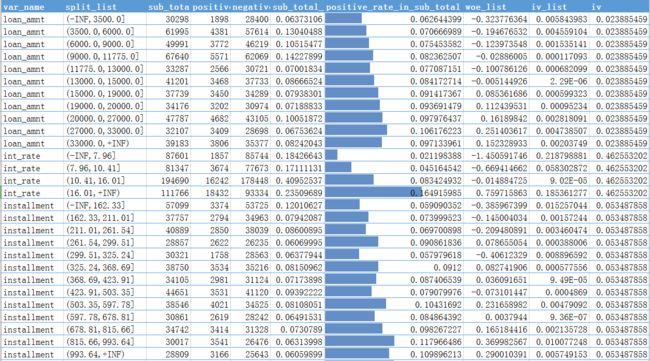
分箱调整:基于positive_rate对相邻分箱进行合并,使其呈现单调性,更贴近业务逻辑,满足模型解释性要求,选择IV值相对较高的变量进行分箱调整
<部分分箱结果>
导入调整后的分箱结果:
bined_adjust=pd.read_csv('C:\\Users\\honglihui\\Desktop\\LendingClubLoanData-UpdateTime201905\\bined_adjust.csv',low_memory=False)
bined_adjust.dropna(axis=[0,1],how='all',inplace=True)
- 变量数值编码
以WOE值代替原始数据:
bined_adjust_con=bined_adjust[:489]#调整后的连续型变量分箱结果
bined_adjust_dis=bined_adjust[489:]#调整后的离散型变量分箱结果
#连续型变量WOE转化:
for var in continuous_col:#连续型变量池
con=bined_adjust_con['split_list'][bined_adjust_con.var_name==var]#取出相应变量的split_list
idx=data.index#初始化index
for i in bined_adjust_con[bined_adjust_con.var_name==var].index:#该变量所对应的分箱index区间
con[i]=con[i].replace('(',' ').replace(')',' ').replace(']',' ').strip().split(',')#将split_list处理成包含区间最大最小值的list
upper=np.float64(con[i][1])#右边值设为区间最大值
lower=np.float64(con[i][0])#左边值设为区间最小值
idx1=data[var][idx][(data[var][idx]>lower) & (data[var][idx]<=upper)].index#该段对应的index
data[var][idx1]=bined_adjust_con.woe_list[i]#选出该段index对应的值以woe值替换
idx=idx[~idx.isin(idx1)]#更新index,已替换过值的index不进入下一次值替换循环
#离散型变量WOE转化:
for var in discrete_col:#离散型变量池
dis=bined_adjust_dis['split_list'][bined_adjust_dis.var_name==var]#取出相应变量的split_list
for i in bined_adjust_dis[bined_adjust_dis.var_name==var].index:#该变量所对应的分箱index区间
dis[i]=dis[i].replace('[','').replace(']','').replace("'",'').strip().split(',')#将split_list处理成包含所有子元素的list
data[var][data[var].isin(dis[i])]=bined_adjust_dis.woe_list[i]#以woe值替换原值
数值编码后的数据集:
data.head()
- 变量选择
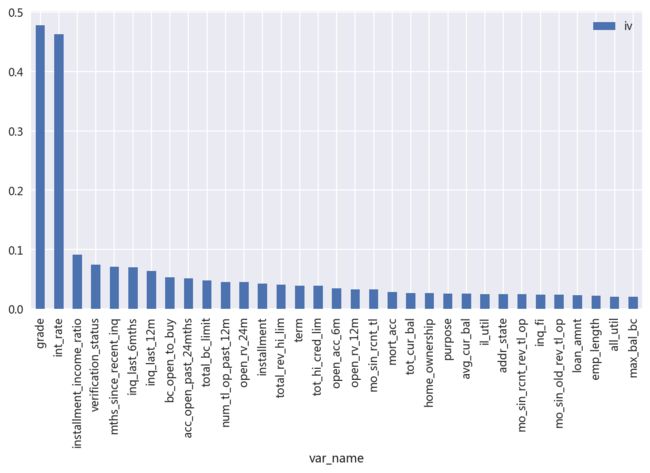
IV=bined_adjust[['var_name','iv']].drop_duplicates()#每个解释变量对应的iv值
vas=IV[['var_name','iv']][IV.iv>0.02].sort_values(by='iv',ascending=False)#筛去iv小于0.02无预测能力的变量
vas.set_index(keys='var_name',inplace=True)
vas.plot(kind='bar',figsize=(10,5))
共筛选出33个解释变量,其中grade与int_rate两个变量的预测能力较强,其余较一般,可以预见最后的模型效果并不会太好
- 变量的相关性分析:
r=data[vas.index].corr()#相关系数
r=r.round(2)
plt.figure(figsize=(15,10))
sns.heatmap(data=r,annot=True)
可以看出有几个变量之间相关性很强,其中tot_cur_bal与tot_hi_cred_lim相关系数0.95,loan_amnt与installment相关系数0.91,均呈现强正相关关系,需要考虑剔除其中一个,以减少多重共线性对Logistic回归的影响
2.变量的多重共线性分析:Logistic回归对多重共线性敏感,利用方差膨胀因子(VIF)来检测多重共线性:若VIF>5,则说明变量间存在较严重的多重共线性
a=data[r.index]#取上面相关分析中用到的变量
b=np.array(a)
VIF=[]
for i in range(a.shape[1]):
vifi=variance_inflation_factor(exog=b,exog_idx=i)#计算方差膨胀因子
VIF.append(vifi)
VIF
- 建模变量选择:
最终基于使模型输出的变量系数均为正以保证解释性、尽可能地缩减变量的数量、选择便于业务解释的变量等原则决定剔除以下这些变量:
v=vas.index
v=v[~v.isin(['tot_cur_bal','loan_amnt','total_bc_limit','avg_cur_bal','open_rv_24m','open_rv_12m',
'num_tl_op_past_12m','total_rev_hi_lim','term','open_acc_6m','mo_sin_old_rev_tl_op',
'all_util','inq_last_12m','bc_open_to_buy','mo_sin_rcnt_tl','mort_acc','il_util',
'mo_sin_rcnt_rev_tl_op','inq_fi'])]#删除这些变量
最终筛选出来用于建模的变量一共14个
五、建立模型
- 训练模型
v=v.insert(0,'target')
data=data[v]#建模数据集,包含14个解释变量,1个目标变量
X=data.drop('target',axis=1)
y=data['target'].astype('int')
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=0)#80%训练集,20%测试集
clf=LogisticRegressionCV(Cs=[0.001,0.01,0.1,1,10,100,1000],#正则化强度备选集
cv=10,#10折交叉验证
class_weight='balanced',#自动调整类别权重
penalty='l2',#选用L2正则化
random_state=0,#设置一个固定的随机数种子
)#其余为默认参数
clf.fit(X_train,y_train)#训练模型
六、模型评估
输出各阈值对应的FPR、TPR:
y_score=clf.predict_proba(X_test)[:,1]#模型输出的正样本概率
fpr,tpr,thresholds=roc_curve(y_test,y_score)
- ROC曲线
AUC=auc(fpr,tpr)
plt.figure(figsize=(7,7))
plt.plot(fpr,tpr,label='AUC=%.2f'%AUC)
plt.plot([0,1],[0,1],'--')
plt.xlim([0,1])
plt.ylim([0,1])
plt.xlabel('False Positive Rate',fontdict={'fontsize':12},labelpad=10)
plt.ylabel('True Positive Rate',fontdict={'fontsize':12},labelpad=10)
plt.title('ROC curve',fontdict={'fontsize':20})
plt.legend(loc=0,fontsize=11)
- K-S曲线
KS=max(tpr-fpr)#KS值
TF_diff=pd.Series(tpr)-pd.Series(fpr)
tpr_best=tpr[TF_diff==TF_diff.max()]
fpr_best=fpr[TF_diff==TF_diff.max()]
thr_best=thresholds[TF_diff==TF_diff.max()]#KS值对应的概率阈值
plt.figure(figsize=(7,7))
plt.plot(thresholds,tpr)
plt.plot(thresholds,fpr)
plt.plot([thr_best,thr_best],[fpr_best,tpr_best],'--')
plt.xlim([thresholds.min(),thresholds.max()-1])
plt.ylim([0,1])
plt.text(0.6,0.75,s='KS=%.2f'%KS,fontdict={'fontsize':12})
plt.text(0.6,0.7,s='thr_best=%.3f'%thr_best,fontdict={'fontsize':12})
plt.xlabel('Threshold',fontdict={'fontsize':12},labelpad=10)
plt.ylabel('Rate',fontdict={'fontsize':12},labelpad=10)
plt.title('K-S curve',fontdict={'fontsize':20})
plt.legend(['True Positive Rate','False Positive Rate'],loc=3)
<对应的最佳阈值为0.503,定义坏客户为违约客户,则预测是否违约的最佳判定原则为:违约估计概率>=0.503判定为违约,违约估计概率<0.503判定为正常>
七、建立评分卡
p为违约概率估计,则:
其中:
- A、B为常数
- β0为模型输出的截距
- β1,…,βn为模型输出的变量系数
假设:Odds为1/20所对应的分值为800分,2Odds时对应分值减少50分
代入:800=A-B*log(1/20)
800-50=A-B*log(2*1/20)
可求得A、B,最后求得总评分Score
b=50/(np.log(2))
a=800+b*np.log(1/20)
- 基准分和分段评分:
v=v.drop('target')#参与建模的解释变量集v
coef=clf.coef_#模型输出系数
intercept=clf.intercept_#模型输出截距
#变量集v与对应系数coef组合:v_coef
df_v=pd.DataFrame(v)
df_coef=pd.DataFrame(coef).T
v_coef=pd.concat([df_v,df_coef],axis=1)
v_coef.columns=['var_name','coef']
#变量集v与对应woe组合:v_woe
v_woe=bined_adjust[bined_adjust.var_name.isin(v)][['var_name','split_list','woe_list']].reset_index(drop=True)
#v_coef与v_woe组合:v_coef_woe
v_coef_woe=pd.merge(v_woe,v_coef)
#构建新列wf:变量系数coef与变量各分组woe的乘积
wf=v_coef_woe['woe_list']*v_coef_woe['coef']
v_coef_woe.insert(loc=4,column='wf',value=wf)
#构建新列score_woe:每个分组对应的子评分
score_woe=v_coef_woe['wf']*(-b)
score_woe=round(score_woe,0)#变量各分段得分
v_coef_woe.insert(loc=5,column='score_woe',value=score_woe)
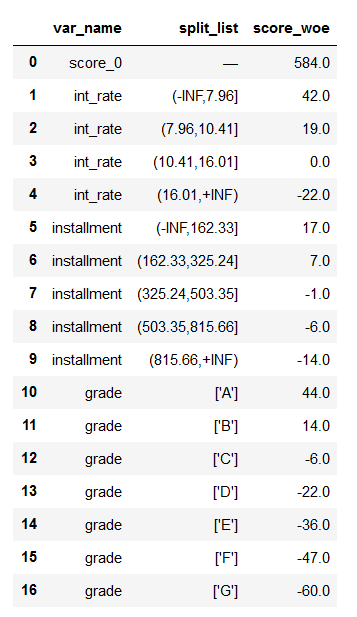
- 合成最终的评分卡:
score_0=round(float(a-b*intercept),0)#基准分
score_X=v_coef_woe[['var_name','split_list','woe_list','score_woe']]#变量中各分段得分
df_score_0=pd.DataFrame(['score_0','—','—','%.f'%score_0],index=['var_name','split_list','woe_list','score_woe']).T
score_card=df_score_0.append(score_X,ignore_index=True)#总评分卡
score_card['score_woe']=score_card['score_woe'].astype('float64')
score_card#输出评分卡
<评分卡部分字段评分>
- 将原始数据以评分形式输出:
data_score=data.copy()#备份data
data_score=data_score.drop('target',axis=1)
for i in v:
coef=v_coef.coef[v_coef.var_name==i].values#变量对应系数
score_woe=(data_score[i]*coef*(-b)).astype('float64')#变量分段对应分数
data_score[i]=round(score_woe,0)
data_score.insert(loc=0,column='score_0',value='%.f'%score_0)#插入基础分值字段
data_score['score_0']=data_score['score_0'].astype('float64')
scores=data_score.sum(axis=1)#计算每个客户总评分
data_score.insert(loc=15,column='scores',value=scores)#插入总评分字段
data_score#输出以评分替换woe后的数据
<部分评分结果>
- 评分数据分析:
draw_score=data_score.copy()#用于画图分析的评分数据副本
proba=clf.predict_proba(X)[:,1]#违约概率估计
target=data['target']#真实标记
draw_score.insert(loc=16,column='proba',value=proba)
draw_score.insert(loc=17,column='target',value=target)
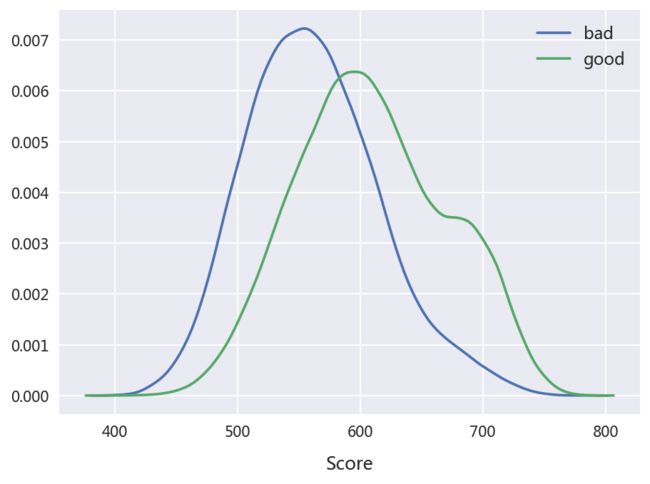
- 好坏客户评分分布情况
bad=draw_score.scores[draw_score.target==1]
good=draw_score.scores[draw_score.target==0]
plt.figure(figsize=(7,5))
sns.distplot(bad,bins=50,hist=False,label='bad')
sns.distplot(good,bins=50,hist=False,label='good')
plt.xlabel('Score',fontdict={'fontsize':12},labelpad=10)
plt.legend(loc=0,fontsize=11)
<坏客户主要分布在550分左右,好客户主要分布在600分左右,有一定区分度,但不明显>
- 评分与违约概率估计
matplotlib.rcParams['agg.path.chunksize']=1000
plt.rcParams['figure.dpi']=150
plt.plot(draw_score.proba,draw_score.scores)
plt.xlabel('Probability estimates')
plt.ylabel('Score')
<评分只是违约概率估计的一个更直观的展现形式,更易于理解和应用,预测的违约概率越低,对应的评分越高>
八、拒绝推论
- 由于从头到尾所用的数据都是已放款的客户数据,模型的建立基于通过的贷款,被拒绝的贷款数据未纳入,因此存在群体上的偏差,若要使模型在整个群体上的预测都有好的表现则需要再进一步优化
- 比如用建立好的模型对拒绝客户群体输出对应分值,挑选部分得分较高的客户标记为好客户,剩下的标记为坏客户,再将所有通过和拒绝的客户数据融合重新建立一个更全面的模型。