树结构基础
LCA
在一棵树中,有a,b二点,求它们的最近公共祖先
dp[i][j]: i往上走2^j步
//初始化
dp[i][0] = fa[i] -> i的祖先(i往上走1(2^0)步)
#include
using namespace std;
const int N = 100010;
const int M = 200010;
int head[N], pnt[M], nxt[M], E;
//head[a]: a这个顶点的边; pnt[j]: j这条边的底点; nxt[i]: i这条边的上一条边; E: 第E条边
int dep[N], dp[N][20];
//初始化
void init(){
E = 0;
memset(head, -1, sizeof(head));
}
//加边
void add(int a, int b){
pnt[E] = b;
nxt[E] = head[a];
head[a] = E++;//更新, 以a为顶点的边(E++)
}
//搜索整棵树, 得到每个节点的深度
void dfs(int u, int f){//u: 一节点 f: 其节点的父亲节点
dep[u] = dep[f] + 1;//深度 父亲节点+1
dp[u][0] = f;//u节点往上1个深度就是其父亲节点
for(int i = head[u]; i != -1; i = nxt[i]){
int v = pnt[i];//u节点为父亲节点, v为孩子节点
if(v != f){
dfs(v, u);//往下搜整棵树
}
}
}
//log(n)时间查询LCA
int ask(int x, int y){
if(dep[x] < dep[y]){//始终保证x在y下面
swap(x, y);
}
int delta = dep[x] - dep[y];//深度差
//先跳到同一高度,x为较深的节点
for(int i = 0; i < 20; i++){//找最小的i, 使2^i <= delta
if(delta & (1 << i)){
x = dp[x][i];
}
}
if(x == y) return x;//二个节点相同, x是y的LCA, 直接返回
for(int i = 19; i >= 0; i--){//从大到小,先跨最大大
if(dp[x][i] != dp[y][i]){
x = dp[x][i];
y = dp[y][i];
}
}
return dp[x][0];//父亲节点还需往上1个深度
}
int main(){
//建树
dfs(1, 0);
for(int i = 1; i < 20; i++){
for(int j = 1; j <= n; j++){
dp[j][i] = dp[dp[j][i-1]][i-1];//2^i = 2^(i-1) + 2^(i-1)
}
}
//查询
return 0;
}
DFS序
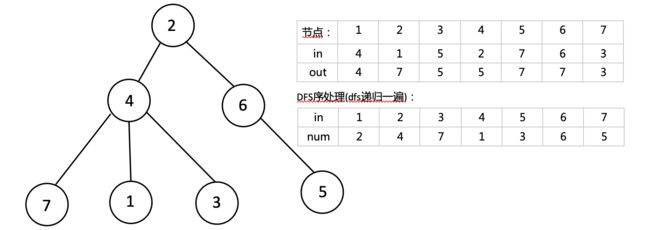
DFS序就是将树形结构转化为线性结构,用dfs遍历一遍这棵树,进入到x节点有一个in时间戳,递归退出时有一个out
时间戳,x节点的两个时间戳之间遍历到的点,就是根为x的子树的所有节点,他们的dfs进入时间戳是递增的。同时两个时间戳构成了一个区间,x节点在这段区间的最左端,这个区间就是一棵根节点为x的子树
……(省略,同LCA)
int L[N], R[N];//每个子树代表的区间
int tot;//总时间
//搜索整棵树, 得到每个节点的深度
void dfs(int u, int f){//u: 一节点 f: 其节点的父亲节点
L[u] = ++tot;
dep[u] = dep[f] + 1;//深度 父亲节点+1
dp[u][0] = f;//u节点往上1个深度就是其父亲节点
for(int i = head[u]; i != -1; i = nxt[i]){
int v = pnt[i];//u节点为父亲节点, v为孩子节点
if(v != f){
dfs(v, u);//往下搜整棵树
}
}
R[u] = tot;
}
……(省略,同LCA)
欧拉序列
对一棵树T进行遍历,无论是递归还是回溯,每次到达一个节点就把编号记录下来,得到一个长度为 2N−1 的序列,成为树 T 的欧拉序列F

序列一:1 2 5 5 6 6 2 3 3 4 4 1
1. 入加出减,前缀和即为到根的权制和
2. 最后一次出现的位置的前缀和减去第一次出现的位置的前缀和即为子树的前缀和
……(省略,同LCA)
int s[N * 2], top;
//搜索整棵树, 得到每个节点的深度
void dfs(int u, int f){//u: 一节点 f: 其节点的父亲节点
s[++top] = u;
dep[u] = dep[f] + 1;//深度 父亲节点+1
dp[u][0] = f;//u节点往上1个深度就是其父亲节点
for(int i = head[u]; i != -1; i = nxt[i]){
int v = pnt[i];//u节点为父亲节点, v为孩子节点
if(v != f){
dfs(v, u);//往下搜整棵树
}
}
s[++top] = -u;
}
……(省略,同LCA)
序列二: 1 2 5 5 2 6 6 2 1 3 3 1 4 4 1
两个点第一次出现的位置之间的区间中深度最小的点就是LCA
……(省略,同LCA)
int s[N * 2], top;
//搜索整棵树, 得到每个节点的深度
void dfs(int u, int f){//u: 一节点 f: 其节点的父亲节点
s[++top] = u;
dep[u] = dep[f] + 1;//深度 父亲节点+1
dp[u][0] = f;//u节点往上1个深度就是其父亲节点
for(int i = head[u]; i != -1; i = nxt[i]){
int v = pnt[i];//u节点为父亲节点, v为孩子节点
if(v != f){
dfs(v, u);//往下搜整棵树
s[++top] = u;//每次加完儿子,都要加一次自己
}
}
s[++top] = -u;
}
……(省略,同LCA)
树的重心
找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心
性质一:树中所有点到某个点到距离之和中,到重心的距离之和是最小的,如果重心有多个则相同
性质二:把两棵树通过一条边相连,新的树的重心在他们的重心的连线上
性质三:把一棵树添加或者删除一个叶子,它的重心最多只移动一条边的距离
性质四:一棵树最多有两个重心,且相邻
树的直径
一棵树中最远的两个点,其路径就是树的直径
性质一:从树中任意一点出发能走到的最远的点一定是S-T中的一点,再从这个点出发就能搜到直径
性质二:所有点直径必定相交于连续的一段
树上差分
差分
一个数组中,一个位置与前一个位置的差
数组a[N], 在L-R中加上V。
利用差分,a[L] = V(a[L]-a[L-1] = V), a[R+1] = -V(a[R+1]-a[R] = -V)
再用前缀和, a[L] - a[R]都视为加上了V
树上差分
每次给一条路径加上值,问最后每条边的权值

