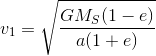Abstract
In this chapter we focus on the solar system.My exercise are about the following two problems.First,investigating the inverse-square force law precisely and see the variation change with the ellipticity; second, using the general relativity adjust the force law and then study the mercury precession, see the variation of eccentricity versus precession angular speed.These two problems are in consistent with problem4.10 and 4.11 in the text book.
Background
As for the planet orbit around sun,by using Newton's law of gravitation and decompose the force into X and Y orientation, we have:
For the sake of ploting and calculating, we choose astronomical unit
we can simply compulate this by using Euler-Cromer method.But in order to calculate we need the initial condition.we let the initial speed perpendicular to the line cross two objects and let the mass ratio of two objects be different.
Under the adjustment of the general relativity, the force law becomes:
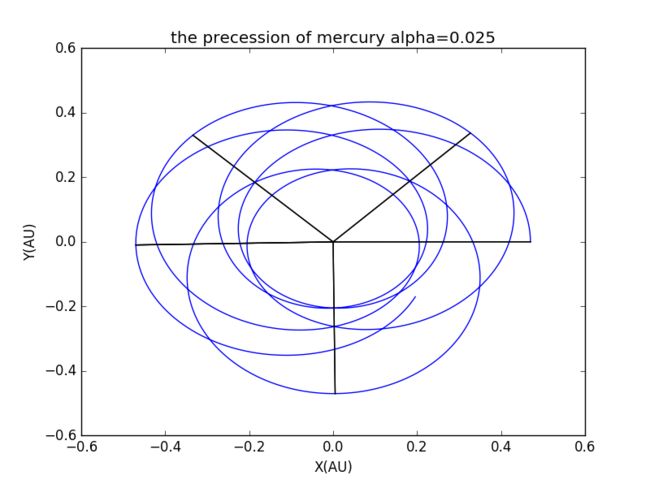
the rate of precession functions as alpha.
Because there are relations between the initial velocity and eccentricity, we can change the initial speed to change the eccentricity.
The Main body
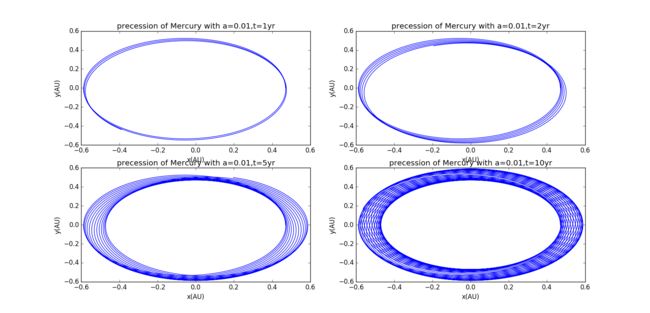
If we change t, the precession of Mercury will be:
Then, we change alpha
click here to see the code
Then we talk about how the precession of the perihelion of a planet' orbit due to general relativity varies as a function of the eccectricity of the orbit
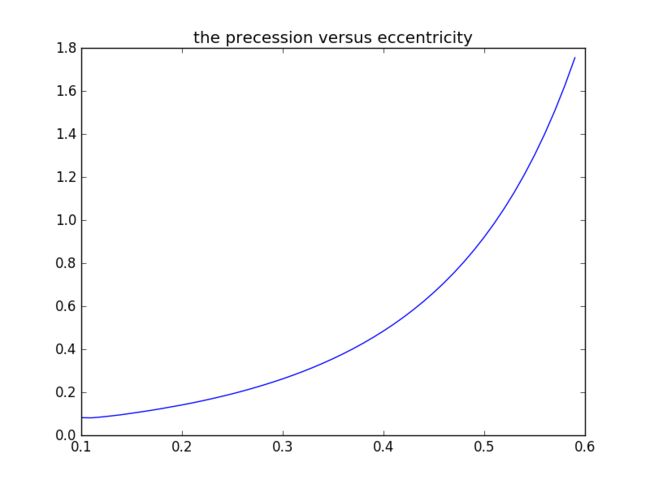
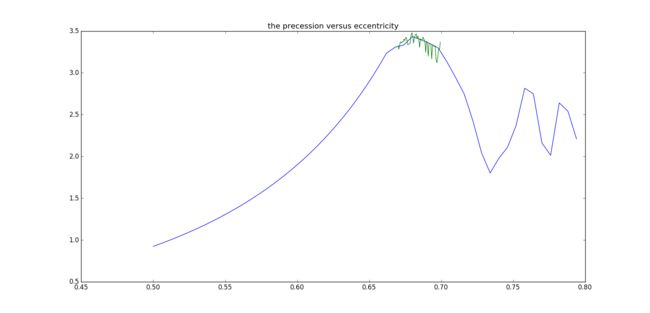
First of all, we plot the precession versus eccentricity.Here the precession is expressed as
Because the limit of accuracy, now we just have a rough glimpse of plot in a 0.1 to 0.8 scale.We find that when eccentricity is over 0.65, there exist wave.
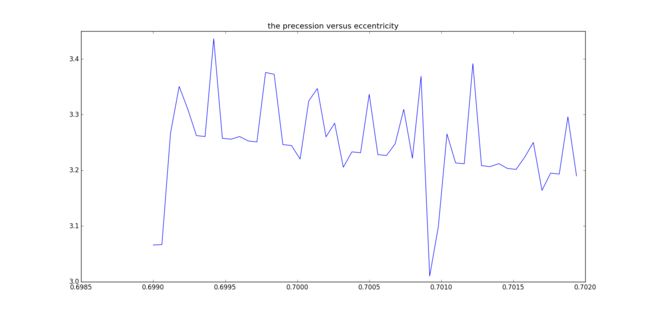
For more details, we have
click here to see the code
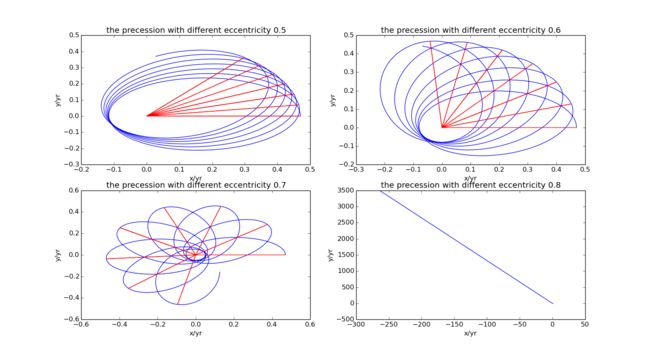
Then we see what happened to the trajectory.
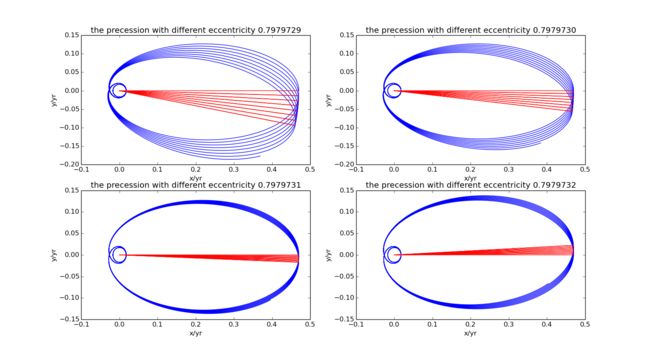
Also, for more details, if we focus on value 0.7979731 of the eccentricity, the precession seems to vanish.
click here to see the code
References
qqyyff' codes