前端 BezierCurves 相关知识
- 代码 github
什么是贝塞尔曲线
只需要很少的控制点就能够生成复杂平滑曲线(更加具体的解释可以搜索一下)
Photoshop的钢笔工具
感知一下
一般不会用到的高深专业参考书
挂钩的前端技术
canvas
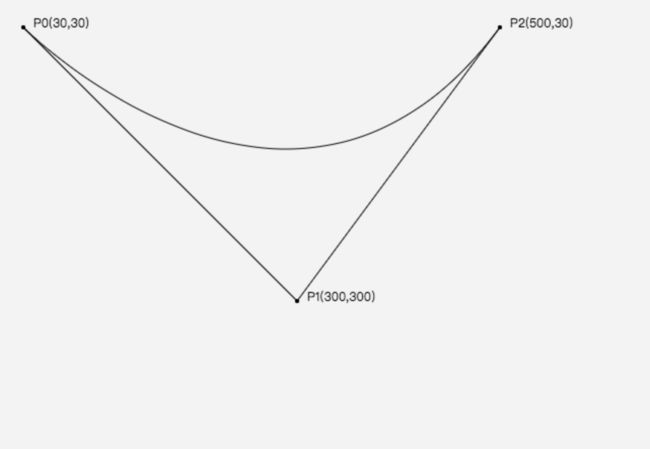
canvas绘制二次贝塞尔曲线 -- quadraticCurveTo(demo2_1)
var myCanvas = document.getElementById('myCanvas');
var myCtx = myCanvas.getContext('2d');
myCtx.beginPath();
myCtx.moveTo(P0.x, P0.y);
//利用quadraticCurveTo 绘制canvas 二次贝塞尔曲线
// 填入控制点(P1) 和 终点(p2)
myCtx.quadraticCurveTo(P1.x, P1.y, P2.x, P2.y);
myCtx.stroke();
myCtx.closePath();
topic_c5_5.png
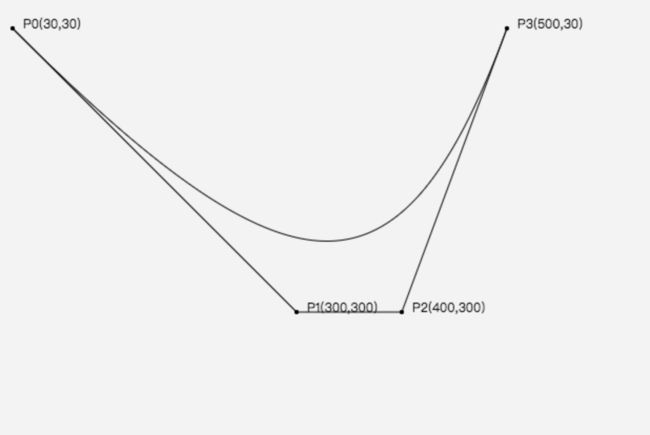
canvas绘制三次贝塞尔曲线 -- bezierCurveTo(demo2_2)
var myCanvas = document.getElementById('myCanvas');
var myCtx = myCanvas.getContext('2d');
myCtx.beginPath();
myCtx.moveTo(P0.x, P0.y);
//利用bezierCurveTo 绘制canvas 三次贝塞尔曲线
// 填入控制点(P1,P2) 和 终点(p3)
myCtx.bezierCurveTo(P1.x, P1.y, P2.x, P2.y, P3.x, P3.y);
myCtx.stroke();
myCtx.closePath();
topic_c5_6.png
svg(demo2_3)
svg -- path 可以绘制贝塞尔曲线
C 后面参数为 控制点P1,控制点P2,以及终点P3
S 后面参数为 控制点P1 和终点P3 (省略了P2)
Q 后面为控制点P1 和终点P2
T 后面为终点P2(省略P1)
L 直线
topic_c5_8.png
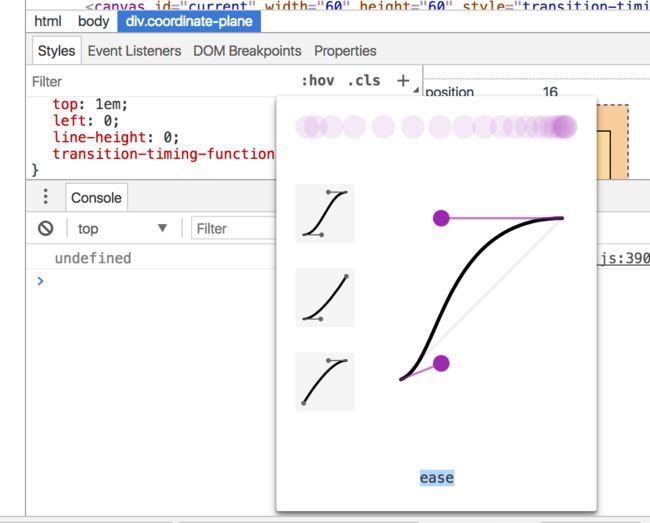
动画 缓动效果(demo2_4)
- css ease 目前chrome浏览器 有内置的工具
特殊的缓懂可以实现一些特殊的效果,例如(Out · Back)
![Uploading topic_c5_1_669418.png . . .]
- canvas 动画也需要 ease效果,各个canvas 动画库都有支持,也涉及一系列动画的算法,不在此展开。
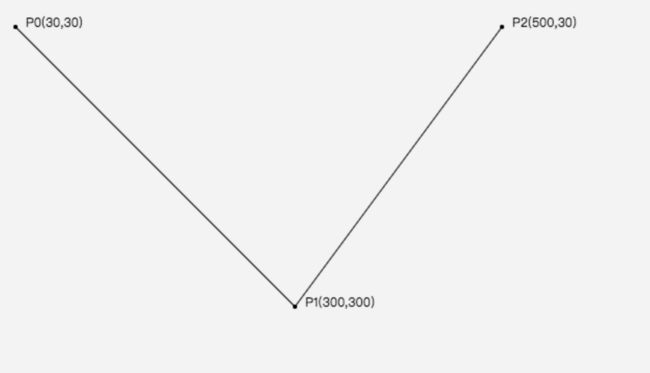
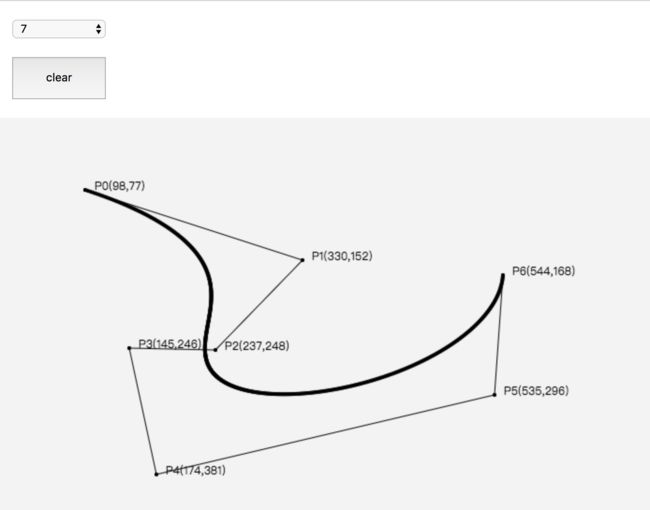
贝塞尔曲线绘制原理(demo1_1)
- 初始化二次贝塞尔曲线的起始点,控制点和终点
var myCanvas = document.getElementById('myCanvas');
var myCtx = myCanvas.getContext('2d');
//初始化3个点
var P0 = {
x: 30,
y: 30,
name: 'P0'
};
var P1 = {
x: 300,
y: 300,
name: 'P1'
};
var P2 = {
x: 500,
y: 30,
name: 'P2'
};
var PointList = [P0, P1, P2];
//绘制三个点
for (var i = 0; i < PointList.length; i++) {
var point = PointList[i];
fillPoint(myCtx, point);
}
//连线P0,P1,P2
linePoint(myCtx, PointList);
function fillPoint(ctx, point) {
if (!ctx || !point) {
return false;
}
ctx.beginPath();
ctx.arc(point.x, point.y, 2, 0, 2 * Math.PI, true);
ctx.fill();
ctx.font = "36px";
ctx.fillText(point.name + '(' + point.x + ',' + point.y + ')', point.x + 10, point.y);
ctx.closePath();
}
function linePoint(ctx, PointList) {
if (!ctx || !PointList.length) {
return false;
}
ctx.beginPath();
for (var i = 0; i < PointList.length; i++) {
var point = PointList[i];
if (i == 0) {
ctx.moveTo(point.x, point.y);
} else {
ctx.lineTo(point.x, point.y);
}
}
ctx.stroke();
ctx.closePath();
}
topic_c5_1.png
-
确定贝塞尔曲线上的某一点
// 随意设置一个比例 var t = 1 / 5; // 在线段P0P1 上找到t比例的点P3, 即 P0P3:P0P1=t; var P3 = { name: 'P3', x: P0.x + (P1.x - P0.x) * t, y: P0.y + (P1.y - P0.y) * t, } fillPoint(myCtx, P3); //在线段P1P2 上找到t距离的点 P4, 即P1P4:P1P2=t; var P4 = { name: 'P4', x: P1.x + (P2.x - P1.x) * t, y: P1.y + (P2.y - P1.y) * t, } fillPoint(myCtx, P4); //连线P3P4 linePoint(myCtx, [P3, P4]); //在线段P3P4 上找到t距离的点P5 即P3P5:P3P4=t; var P5 = { name: 'P5', x: P3.x + (P4.x - P3.x) * t, y: P3.y + (P4.y - P3.y) * t, } fillPoint(myCtx, P5); console.log('P5 在P0P2 为起点终点,P1为控制点的 二次贝塞尔曲线上');
topic_c5_2.png
-
将一个点 循环成曲线
var precision = 500; for (var i = 0; i < precision; i++) { var t = i / precision; getBezierPoint(t); } // 根据t获得贝塞尔曲线上面的点 function getBezierPoint(t) { // 在线段P0P1 上找到t比例的点P3, 即 P0P3:P0P1=t; var P3 = getTPoint(myCtx, P0, P1, t, {needfill: false}) //在线段P1P2 上找到t距离的点 P4, 即P1P4:P1P2=t; var P4 = getTPoint(myCtx, P1, P2, t, {needfill: false}); //在线段P3P4 上找到t距离的点P5 即P3P5:P3P4=t; var P5 = getTPoint(myCtx, P3, P4, t); return P5; } /* * 在线段P0P1 上找到点TP, 使P0TP:P0P1=t, 并绘制出来然后返回点 * */ function getTPoint(myCtx, P0, P1, t, option) { var needfill = true, name = ''; if (option) { needfill = typeof option.needfill == 'boolean' ? option.needfill : true; name = option.name || ''; } var TP = { name: name, x: P0.x + (P1.x - P0.x) * t, y: P0.y + (P1.y - P0.y) * t, } if (needfill) { fillPoint(myCtx, TP); } return TP; }
topic_c5_3.png
- 依次类推到三次贝塞尔曲线
由二次贝塞尔曲线变成多次贝塞尔曲线,原理是一样的,一层套一层,一个迭代的关系
将 getBezierPoint 重写,plist将大于等于3 (demo1_4)
// 根据t获得贝塞尔曲线上面的点
function getBezierPoint(plist, t) {
var newlist = [];
for (var i = 0; i < plist.length - 1; i++) {
var p = getTPoint(myCtx, plist[i], plist[i + 1], t, {needFill: false});
newlist.push(p);
}
if (newlist.length > 1) {
return getBezierPoint(newlist, t);
} else {
return newlist[0];
}
}
topic_c5_4.png
代码仓库(https://github.com/Lotuslwb/BezierCurves)
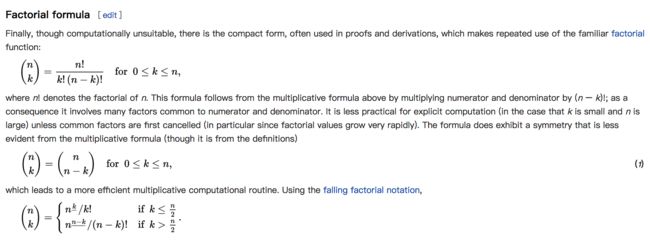
使用公式绘制贝塞尔曲线
topic_c5_9.png
topic_c5_10.png
topic_c5_11.png
(n k) 是什么呢
Binomial_coefficient
topic_c5_12.png
- n=5:第一个系数（5 0）=5！/（0！5！）=1。第二个系数（5 1）=5！/（1！4！）=5。第三个系数（5 2）=5！/（2！3！）=10。接下来是对称的
function binomial(n, k) {
if ((typeof n !== 'number') || (typeof k !== 'number'))
return false;
var coeff = 1;
for (var x = n-k+1; x <= n; x++) coeff *= x;
for (x = 1; x <= k; x++) coeff /= x;
return coeff;
}
多次贝塞尔曲线的公式js版本
function BezierFunction(plist, t) {
if (t > 1 || t < 0) {
return false;
}
// B(t)=P0*(1-t)^5 + 5*P1*t*(1-t)^4+10*P2*t^2(1-t)^3+10*P3*t^3(1-t)^2+ 5*P4*t^4*(1-t)^1+P5*t^5
// 从 0 开始 到 P(n-1) ~~ 3个点 为 2次贝塞尔曲线
var n = plist.length - 1;
var bt = 0;
for (var i = 0; i <= n; i++) {
bt += getBinomial(n, i) * plist[i] * Math.pow((1 - t), (n - i)) * Math.pow(t, i);
return bt;
}
}
绘制贝塞尔曲线动画(demo4_1)
只需要将曲线的实现 简化为点的运动就可以了
drawKeyframe()
function drawKeyframe() {
currentPrecision++;
if (currentPrecision <= maxPrecision) {
myCtx.clearRect(0, 0, myCanvas.width, myCanvas.height);
//绘制三个点
for (var i = 0; i < PointList.length; i++) {
var point = PointList[i];
fillPoint(myCtx, point);
}
//连线P0,P1,P2
linePoint(myCtx, PointList);
var p = getBezierPoint(currentPrecision/maxPrecision);
drawBall(myCtx, p, 10);
window.requestAnimationFrame(drawKeyframe);
}
}
function drawBall(ctx, point, r) {
ctx.beginPath();
ctx.arc(point.x, point.y, r, 0, 2 * Math.PI, true);
ctx.fill();
ctx.closePath();
}
// 根据t获得贝塞尔曲线上面的点
function getBezierPoint(t) {
var p = {
x: quadraticBezierFunction(P0.x, P1.x, P2.x, t),
y: quadraticBezierFunction(P0.y, P1.y, P2.y, t)
};
return p;
}
如何绘制平滑的贝塞尔曲线(获取合理的控制点)
百度地图 计算获取控制点(demo4_2)
function getControlPoint() {
var p0 = PointList[0]; //起始点
var p2 = PointList[1]; //终止点
var curveness = 0.3; //边的曲度
var inv = 1;
var p1 = {
'name': 'P1',
'x': (p0.x + p2.x) / 2 - inv * (p0.y - p2.y) * curveness,
'y': (p0.y + p2.y) / 2 - inv * (p0.x - p2.x) * curveness
};
p2.name = 'P2';
PointList.splice(1, 0, p1);
for (var i = 0; i < PointList.length; i++) {
var p = PointList[i];
PointListX.push(p.x);
PointListY.push(p.y);
}
}
贝塞尔曲线的一些应用
canvas 大波浪动效
用大波浪做loading, qq的例子 如下, 文章链接
topic_c5_4.gif
- 先用canvas + quadraticCurveTo 画出波浪曲线(demo5_1)
var myCanvas = document.getElementById('myCanvas');
var myCtx = myCanvas.getContext('2d');
var canvasHeight = myCanvas.height, canvasWidth = myCanvas.width;
var animationFrame;
//半波长
var waveLen = 100, waveHeight = 30;
//水位线初始点
var p0 = {
x: 0,
y: canvasHeight / 2
};
drawKeyframe();
function drawKeyframe() {
//记录当前位置
var currentX = p0.x, currentY = p0.y;
myCtx.clearRect(0, 0, canvasWidth, canvasHeight);
myCtx.beginPath();
myCtx.moveTo(p0.x, p0.y);
for (var i = 0; currentX <= canvasWidth + waveLen; i++) {
if (i % 2 == 0) {
//上半部波
myCtx.quadraticCurveTo(currentX + waveLen, currentY - waveHeight, currentX + waveLen * 2, currentY);
} else {
//下半部波
myCtx.quadraticCurveTo(currentX + waveLen, currentY + waveHeight, currentX + waveLen * 2, currentY);
}
currentX += waveLen * 2;
myCtx.moveTo(currentX, currentY)
}
myCtx.lineWidth = 5;
myCtx.fillStyle = "red";
myCtx.lineTo(canvasWidth, canvasHeight);
myCtx.lineTo(0, canvasHeight);
myCtx.lineTo(0, canvasHeight / 2);
myCtx.fill();
myCtx.closePath();
p0.x -= 5;
animationFrame = window.requestAnimationFrame(drawKeyframe);
}
- 增加动画 效果 (demo5_2)
topic_c5_13.gif
贝塞尔曲线拟合计算
贝塞尔曲线有一个非常常用的动画效果——MetaBall算法。
相信很多开发者都见过类似的动画，例如QQ的小红点消除，下拉刷新loading等等。
要做好这个动画，实际上最重要的就是通过贝塞尔曲线来拟合两个图形。
topic_c5_14.png
- 矩形拟合 (demo5_3)
控制点为两圆圆心连线的中点，
连接线为图中的这样一个矩形，
当圆比较小时，这种通过矩形来拟合的方式几乎是没有问题的。
我们把圆放大,就会不拟合。
// 圆R0 圆点
var p0 = {
x: 120,
y: 120,
r: 20
};
// 圆R1 圆点
var p1 = {
x: 400,
y: 400,
r: 20
};
//获得 R0 和 R1 的中点
var p2 = {
x: (p0.x + p1.x) / 2,
y: (p0.y + p1.y) / 2,
name: 'p2'
};
myCtx.beginPath();
//画出2个圆
myCtx.arc(p0.x, p0.y, p0.r, 0, 2 * Math.PI, true);
myCtx.stroke();
myCtx.closePath();
myCtx.beginPath();
myCtx.arc(p1.x, p1.y, p1.r, 0, 2 * Math.PI, true);
myCtx.stroke();
myCtx.closePath();
//画出中点和圆心连线
linePoint(myCtx, [p0, p1]);
fillPoint(myCtx, p2);
// p0 的2个端点
var p0_1 = {
x: p0.x - p0.r / Math.sqrt(2),
y: p0.y + p0.r / Math.sqrt(2),
name: 'p0_1'
}, p0_2 = {
x: p0.x + p0.r / Math.sqrt(2),
y: p0.y - p0.r / Math.sqrt(2),
name: 'p0_2'
};
linePoint(myCtx, [p0_1, p0_2]);
fillPoint(myCtx, p0_1);
fillPoint(myCtx, p0_2);
//p1 的2个端点
var p1_1 = {
x: p1.x - p1.r / Math.sqrt(2),
y: p1.y + p1.r / Math.sqrt(2),
name: 'p1_1'
}, p1_2 = {
x: p1.x + p1.r / Math.sqrt(2),
y: p1.y - p1.r / Math.sqrt(2),
name: 'p1_2'
};
linePoint(myCtx, [p1_1, p1_2]);
fillPoint(myCtx, p1_1);
fillPoint(myCtx, p1_2);
// 连接2个圆的端点
linePoint(myCtx, [p0_1, p1_1]);
linePoint(myCtx, [p0_2, p1_2]);
//绘制曲线
myCtx.beginPath();
myCtx.strokeStyle = 'red';
myCtx.moveTo(p0_1.x, p0_1.y);
myCtx.quadraticCurveTo(p2.x, p2.y, p1_1.x, p1_1.y);
myCtx.stroke();
myCtx.closePath();
myCtx.beginPath();
myCtx.strokeStyle = 'red';
myCtx.moveTo(p0_2.x, p0_2.y);
myCtx.quadraticCurveTo(p2.x, p2.y, p1_2.x, p1_2.y);
myCtx.stroke();
myCtx.closePath();
- 切线拟合(demo5_5)
如前面所说，矩形拟合在半径较小的情况下，是可以实现完美拟合的，而当半径变大后，就会出现贝塞尔曲线与圆相交的情况，导致拟合失败。
那么如何来实现完美的拟合呢？实际上，也就是说贝塞尔曲线与圆的连接点到贝塞尔曲线的控制点的连线，一定是圆的切线，这样的话，无论圆的半径如何变化，贝塞尔曲线一定是与圆拟合的，具体效果如图所示：
topic_c5_15.jpeg
// 获取切点坐标 数组,经过圆外一点有2个切点
//p0 为圆心1, p1圆心1, p2为2圆中点,r为圆的半径
function getTangencyPoint(p0, p1, p2, r, sencond) {
//获取小角 角度
var x = Math.abs(p0.x - p1.x);
var y = Math.abs(p0.y - p1.y);
var angles1 = Math.atan(y / x);
if (sencond) {
angles1 = Math.PI - angles1;
}
//获取大角 角度
//中点到圆点的距离
var len = Math.sqrt((p0.x - p2.x) * (p0.x - p2.x) + (p0.y - p2.y) * (p0.y - p2.y));
var angles2 = Math.acos(r / len);
//获得需要的角度
var angles3 = Math.abs(angles2 - angles1);
//获取距离圆心的距离
var diffx = Math.cos(angles3) * r;
var diffy = Math.sin(angles3) * r;
return [{
x: p0.x - diffy,
y: p0.y + diffx
}, {
x: p0.x + diffx,
y: p0.y - diffy
}]
}
- 最终效果 (demo5_7)
topic_c5_15.gif