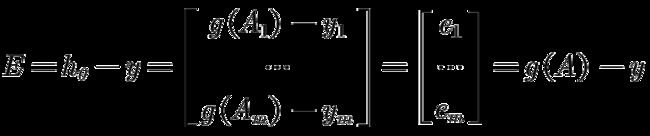
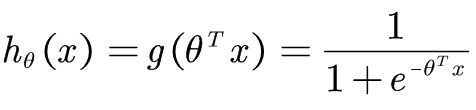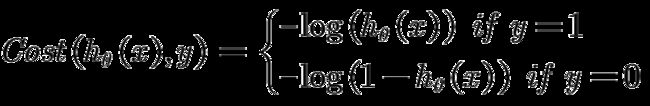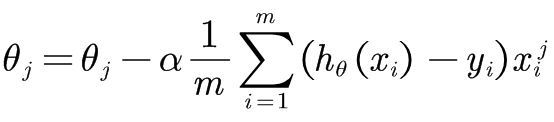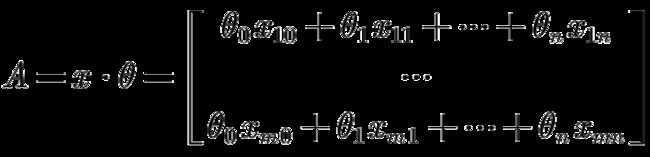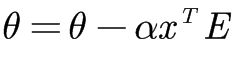- 梯度提升决策树树(GBDT)公式推导
化作星辰
决策树算法机器学习
###逻辑回归的损失函数逻辑回归模型用于分类问题,其输出是一个概率值。对于二分类问题,逻辑回归模型的输出可以表示为:\[P(y=1|x)=\frac{1}{1+e^{-F(x)}}\]其中\(F(x)\)是一个线性组合函数,通常表示为:\[F(x)=\sum_{m=0}^{M}h_m(x)\]这里的\(h_m(x)\)是学习到的决策树。###损失函数的推导对于单个样本\((x_i,y_i)\),逻
- R数据分析:多分类问题预测模型的ROC做法及解释
公众号Codewar原创作者
R数据分析
有同学做了个多分类的预测模型,结局有三个类别,做的模型包括多分类逻辑回归、随机森林和决策树,多分类逻辑回归是用ROC曲线并报告AUC作为模型评估的,后面两种模型报告了混淆矩阵,审稿人就提出要统一模型评估指标。那么肯定是统一成ROC了,刚好借这个机会给大家讲讲ROC在多分类问题情形下的具体使用和做法。ROC曲线回顾ROC曲线(ReceiverOperatingCharacteristicCurve)
- 机器算法之逻辑回归(Logistic Regression)详解
HappyAcmen
算法合集算法逻辑回归机器学习
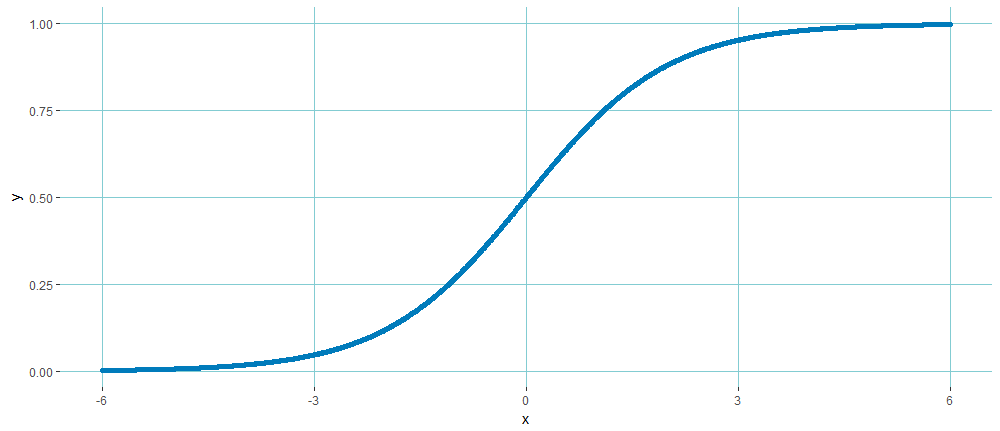
一、什么是逻辑回归?逻辑回归并不是传统意义上的回归分析,而是一种用于处理二分类问题的线性模型。它通过计算样本属于某一类别的概率来进行分类,尽管名字中有“回归”二字,但它实际上是一种分类算法。简单来说,逻辑回归回答的是“这件事发生的可能性有多大”。二、逻辑回归的基本原理在讲原理之前,我们先来了解一下逻辑回归的数学基础。逻辑回归的核心是一个Logistic函数(或称为Sigmoid函数),它的公式如下
- 机器学习——逻辑回归
口_天_光健
python机器学习逻辑回归
逻辑回归技术文档目录简介逻辑回归的基本概念逻辑回归的数学原理逻辑回归的实现步骤代码示例逻辑回归的应用逻辑回归的优化方法逻辑回归的局限性逻辑回归的扩展与变体逻辑回归与其他算法的对比总结简介逻辑回归(LogisticRegression)是一种广泛应用于分类问题的统计方法。尽管名字中有“回归”二字,但逻辑回归实际上是一种分类算法,主要用于二分类问题,但也可以通过扩展用于多分类问题。逻辑回归通过使用逻辑
- 【华为OD技术面试真题 - 技术面】- python八股文真题题库(1)
算法大师
华为od面试python
华为OD面试真题精选专栏:华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.数据预处理流程数据预处理的主要步骤工具和库2.介绍线性回归、逻辑回归模型线性回归(LinearRegression)模型形式:关键点:逻辑回归(LogisticRegression)模型形式:关键点:参数估计与评估:3.python浅拷贝及深拷贝浅拷贝(Shal
- Python实现简单的机器学习算法
master_chenchengg
pythonpython办公效率python开发IT
Python实现简单的机器学习算法开篇:初探机器学习的奇妙之旅搭建环境:一切从安装开始必备工具箱第一步:安装Anaconda和JupyterNotebook小贴士:如何配置Python环境变量算法初体验:从零开始的Python机器学习线性回归:让数据说话数据准备:从哪里找数据编码实战:Python实现线性回归模型评估:如何判断模型好坏逻辑回归:从分类开始理论入门:什么是逻辑回归代码实现:使用skl
- 几率odds与逻辑回归
元气小地瓜
https://www.jianshu.com/p/aa73938f32ee几率odds从Odds角度理解LogisticRegression模型的参数13December20151.引言无论在学术界,还是在工业界,LogisticRegression(LR,逻辑回归)模型[1]是常用的分类模型,被用于各种分类场景和点击率预估问题等,它也是MaxEntropy(ME,最大熵)模型[2],或者说So
- 分类算法可视化方法
dundunmm
数据挖掘分类数据挖掘人工智能可视化
可视化方法可以用于帮助理解分类算法的决策边界、性能和在不同数据集上的行为。下面列举几个常见的可视化方法。1.决策边界可视化这种方法用于可视化不同分类算法在二维特征空间中如何分隔不同类别。对于理解决策树、支持向量机(SVM)、逻辑回归和k近邻(k-NN)等模型的行为非常有用。importnumpyasnpimportmatplotlib.pyplotaspltfromsklearn.datasets
- 【机器学习】广义线性模型(GLM)的基本概念以及广义线性模型在python中的实例(包含statsmodels和scikit-learn实现逻辑回归)
Lossya
机器学习pythonscikit-learn线性回归人工智能逻辑回归
引言GLM扩展了传统的线性回归模型,使其能够处理更复杂的数据类型和分布文章目录引言一、广义线性模型1.1定义1.2广义线性模型的组成1.2.1响应变量(ResponseVariable)1.2.2链接函数(LinkFunction)1.2.3线性预测器(LinearPredictor)1.3常见的广义线性模型1.3.1线性回归1.3.2逻辑回归1.3.3泊松回归1.4GLM的特性1.5广义线性模型
- 机器学习实战笔记5——线性判别分析
绍少阿
机器学习笔记可视化机器学习python人工智能
任务安排1、机器学习导论8、核方法2、KNN及其实现9、稀疏表示3、K-means聚类10、高斯混合模型4、主成分分析11、嵌入学习5、线性判别分析12、强化学习6、贝叶斯方法13、PageRank7、逻辑回归14、深度学习线性判别分析(LDA)Ⅰ核心思想对于同样一件事,站在不同的角度,我们往往会有不同的看法,而降维思想,亦是如此。同上节课一样,我们还是学习降维的算法,只是提供了一种新的角度,由上
- 亦菲喊你来学机器学习(20) --PCA数据降维
方世恩
机器学习人工智能深度学习python算法sklearn
文章目录PCA数据降维一、降维二、优缺点三、参数四、实例应用1.读取文件2.分离特征和目标变量3.使用PCA进行降维4.打印特征所占百分比和具体比例5.PCA降维后的数据6.划分数据集7.训练逻辑回归模型8.评估模型性能总结PCA数据降维主成分分析(PrincipalComponentAnalysis,PCA)是一种常用的数据降维技术,它可以在保留数据集中最重要的特征的同时,减少数据的维度。PCA
- R语言多项逻辑回归-因变量是无序多分类
医学和生信笔记
医学统计学r语言医学统计学
因变量是无序多分类资料(>2)时,可使用多分类逻辑回归(multinomiallogisticregression)。使用课本例16-5的数据,课本电子版及数据已上传到QQ群,自行下载即可。某研究人员欲了解不同社区和性别之间居民获取健康知识的途径是否相同,对2个社区的314名成人进行了调查,其中X1是社区,社区1用0表示,社区2用1表示;X2是性别,0是男,1是女,Y是获取健康知识途径,1是传统大
- 备战2024数学建模国赛(模型三十):遗传算法 优秀案例(三) 变循环发动机部件法建模及优化
2024年数学建模国赛
备战2024数学建模国赛2024数学建模(不代写论文请勿盲目订阅)数学建模2024年数学建模国赛备战数学建模国赛算法遗传算法2024
专栏内容(赛前预售价99,比赛期间299):2024数学建模国赛期间会发布思路、代码和优秀论文。(本专栏达不到国一的水平,适用于有一点点基础冲击省奖的同学,近两年有二十几个国二,但是达不到国一,普遍获得省奖,请勿盲目订阅)python全套教程(一百篇博客):从新手到掌握使用python,可以对数学建模问题进行建模分析。35套模型算法(优秀论文示例):马尔科夫模型、遗传算法、逻辑回归、逐步回归、蚁群
- R实现线性回归逻辑回归
weixin_55475210
r语言线性回归逻辑回归
线性回归基本模型Y=β0+β1X1+β2X2+⋯+βmXm+ϵY=\beta_0+\beta_1X_1+\beta_2X_2+\cdots+\beta_mX_m+\epsilonY=β0+β1X1+β2X2+⋯+βmXm+ϵYYY为因变量X1,X2,…,XmX_1,X_2,\ldots,X_mX1,X2,…,Xm为m个自变量ϵ\epsilonϵ为残差lm()函数用于完成多元线性回归系数估计,回归系
- 备战2024数学建模国赛(模型十五):模糊综合评价 优秀案例(一)确定汽车装配顺序问题的算法
2024年数学建模国赛
备战2024数学建模国赛2024数学建模(持续更新耐心等待)数学建模汽车算法2024数学建模国赛备战2024数学建模国赛模糊综合评价模型
专栏内容(赛前预售价99,比赛期间299):2024数学建模国赛期间会发布思路、代码和优秀论文。(本专栏达不到国一的水平,适用于有一点点基础冲击省奖的同学,近两年有二十几个国二,但是达不到国一,普遍获得省奖,请勿盲目订阅)python全套教程(一百篇博客):从新手到掌握使用python,可以对数学建模问题进行建模分析。35套模型算法(优秀论文示例):马尔科夫模型、遗传算法、逻辑回归、逐步回归、蚁群
- 备战2024数学建模国赛(模型十九):排队论 优秀案例(一)火车票购票网站优化
2024年数学建模国赛
备战2024数学建模国赛备战2024数学建模数学建模2024年数学建模国赛2024数学建模国赛马尔科夫模型排队论
专栏内容(赛前预售价99,比赛期间299):2024数学建模国赛期间会发布思路、代码和优秀论文。(本专栏达不到国一的水平,适用于有一点点基础冲击省奖的同学,近两年有二十几个国二,但是达不到国一,普遍获得省奖,请勿盲目订阅)python全套教程(一百篇博客):从新手到掌握使用python,可以对数学建模问题进行建模分析。35套模型算法(优秀论文示例):马尔科夫模型、遗传算法、逻辑回归、逐步回归、蚁群
- 备战2024数学建模国赛(模型二十五):微分方程 优秀案例(一)基于非稳态导热的高温作业专用服装设计
2024年数学建模国赛
备战2024数学建模国赛备战2024数学建模数学建模人工智能备战2024数学建模国赛深度学习数学建模国赛2024
专栏内容(赛前预售价99,比赛期间299):2024数学建模国赛期间会发布思路、代码和优秀论文。(本专栏达不到国一的水平,适用于有一点点基础冲击省奖的同学,近两年有二十几个国二,但是达不到国一,普遍获得省奖,请勿盲目订阅)python全套教程(一百篇博客):从新手到掌握使用python,可以对数学建模问题进行建模分析。35套模型算法(优秀论文示例):马尔科夫模型、遗传算法、逻辑回归、逐步回归、蚁群
- 备战2024数学建模国赛(模型四):动态规划优秀案例(一)基于蒙特卡洛模拟的眼科病床安排排队模型
2024年数学建模国赛
备战2024数学建模国赛备战2024数学建模数学建模动态规划算法20242024年数学建模国赛备战数学建模竞赛matlab
专栏内容(赛前预售价99,比赛期间299):2024数学建模国赛期间会发布思路、代码和优秀论文。(本专栏达不到国一的水平,适用于有一点点基础冲击省奖的同学,近两年有二十几个国二,但是达不到国一,普遍获得省奖,请勿盲目订阅)python全套教程(一百篇博客):从新手到掌握使用python,可以对数学建模问题进行建模分析。35套模型算法(优秀论文示例):马尔科夫模型、遗传算法、逻辑回归、逐步回归、蚁群
- 推荐Rerank二次重排序算法
陈敬雷-充电了么-CEO兼CTO
算法人工智能hadoop机器学习人工智能大数据数据挖掘编程语言
注:此文章内容均节选自充电了么创始人,CEO兼CTO陈敬雷老师的新书《自然语言处理原理与实战》(人工智能科学与技术丛书)【陈敬雷编著】【清华大学出版社】推荐Rerank二次重排序算法前言推荐的Rerank排序有两种情况,一个是离线计算的时候为每个用户提前用Rerank排序算法算好推荐结果,另一个是在实时在线Web推荐引擎里做二次融合排序的时候。但不管哪一种用到的算法是一样的。比如用逻辑回归、随机森
- python logistic regression_机器学习算法与Python实践之逻辑回归(Logistic Regression)
weixin_39702649
pythonlogisticregression
机器学习算法与Python实践这个系列主要是参考下载地址:https://bbs.pinggu.org/thread-2256090-1-1.html一、逻辑回归(LogisticRegression)Logisticregression(逻辑回归)是当前业界比较常用的机器学习方法,用于估计某种事物的可能性。之前在经典之作《数学之美》中也看到了它用于广告预测,也就是根据某广告被用户点击的可能性,把
- Logistic分类算法原理及Python实践
doublexiao79
数据分析与挖掘分类python数据挖掘
一、Logistic分类算法原理Logistic分类算法,也称为逻辑回归(LogisticRegression),是机器学习中的一种经典分类算法,主要用于解决二分类问题。其原理基于线性回归和逻辑函数(Sigmoid函数)的组合,能够将输入特征的线性组合映射到一个概率范围内,从而进行分类预测。以下是Logistic分类算法的主要原理:1.线性组合首先,对于输入的n个特征,我们将其表示为一个n维的列向
- python logistic模型_Python实践之逻辑回归(Logistic Regression)
weixin_39922394
pythonlogistic模型
机器学习算法与Python实践这个系列主要是参考《机器学习实战》这本书。因为自己想学习Python,然后也想对一些机器学习算法加深下了解,所以就想通过Python来实现几个比较常用的机器学习算法。恰好遇见这本同样定位的书籍,所以就参考这本书的过程来学习了。这节学习的是逻辑回归(LogisticRegression),也算进入了比较正统的机器学习算法。啥叫正统呢?我概念里面机器学习算法一般是这样一个
- 备战2024数学建模国赛(模型十八):拟合模型 优秀案例(二)高温作业服设计
2024年数学建模国赛
备战2024数学建模国赛备战2024数学建模数学建模2024年数学建模国赛数学建模国赛算法拟合模型
专栏内容(赛前预售价99,比赛期间299):2024数学建模国赛期间会发布思路、代码和优秀论文。(本专栏达不到国一的水平,适用于有一点点基础冲击省奖的同学,近两年有二十几个国二,但是达不到国一,普遍获得省奖,请勿盲目订阅)python全套教程(一百篇博客):从新手到掌握使用python,可以对数学建模问题进行建模分析。35套模型算法(优秀论文示例):马尔科夫模型、遗传算法、逻辑回归、逐步回归、蚁群
- 备战2024数学建模国赛(模型六):多元回归 优秀案例(一)颜色与物质浓度的辨识问题
2024年数学建模国赛
备战2024数学建模国赛备战2024数学建模数学建模多元回归2024数学建模国赛2024matlab备战数学建模国赛国赛思路代码
专栏内容(赛前预售价99,比赛期间299):2024数学建模国赛期间会发布思路、代码和优秀论文。(本专栏达不到国一的水平,适用于有一点点基础冲击省奖的同学,近两年有二十几个国二,但是达不到国一,普遍获得省奖,请勿盲目订阅)python全套教程(一百篇博客):从新手到掌握使用python,可以对数学建模问题进行建模分析。35套模型算法(优秀论文示例):马尔科夫模型、遗传算法、逻辑回归、逐步回归、蚁群
- 深度学习100问13:什么是二分类问题
不断持续学习ing
人工智能机器学习自然语言处理
嘿,你知道二分类问题不?这就像是一个“超级裁判”,要把东西分成两大类。一、定义及举例想象一下,生活中有很多时候我们得决定一个东西到底属于哪一边。就像判断一封邮件,是“垃圾邮件”呢,还是“正常邮件”;或者看看一个病人,是“得了某种病”呢,还是“没得病”。二、解决方法要解决二分类问题呀,我们可以找来一些“魔法工具”,也就是机器学习算法。像逻辑回归啦、支持向量机啦、决策树啦等等。这些算法就像聪明的小助手
- 机器学习算法深度总结(5)-逻辑回归
婉妃
1.模型定义逻辑回归属于基于概率分类的学习法.基于概率的模式识别是指对模式x所对应的类别y的后验概率禁行学习.其所属类别为后验概率最大时的类别:预测类别的后验概率,可理解为模式x所属类别y的可信度.逻辑回归(logistic),使用线性对数函数对分类后验概率进行模型化:上式,分母是满足概率总和为1的约束条件的正则化项,参数向量维数为:考虑二分类问题:使用上述关系式,logistic模型的参数个数从
- 【ShuQiHere】从零开始实现逻辑回归:深入理解反向传播与梯度下降
ShuQiHere
代码武士的机器学习秘传逻辑回归算法机器学习
【ShuQiHere】逻辑回归是机器学习中一个经典的分类算法,尽管它的名字中带有“回归”,但它的主要用途是处理二分类问题。逻辑回归通过一个逻辑函数(Sigmoid函数)将输入特征映射到一个概率值上,然后根据这个概率值进行分类。本文将带你从零开始一步步实现逻辑回归,并深入探讨背后的核心算法——反向传播与梯度下降。逻辑回归的数学基础逻辑回归的目标是找到一个逻辑函数,能够将输入特征映射到一个(0,1)之
- 【ShuQiHere】《机器学习的进化史『下』:从神经网络到深度学习的飞跃》
ShuQiHere
机器学习深度学习神经网络
【ShuQiHere】引言:神经网络与深度学习的兴起在上篇文章中,我们回顾了机器学习的起源与传统模型的发展历程,如线性回归、逻辑回归和支持向量机(SVM)。然而,随着数据规模的急剧增长和计算能力的提升,传统模型在处理复杂问题时显得力不从心。在这种背景下,神经网络重新进入了研究者们的视野,并逐步演变为深度学习,成为解决复杂问题的强大工具。今天,我们将进一步探索从神经网络到深度学习的进化历程,揭示这些
- 机器学习(ML)算法分类
活蹦乱跳酸菜鱼
机器学习
机器学习(ML)算法是一个广泛而多样的领域,涵盖了多种用于数据分析和模式识别的技术。以下是一些常见的机器学习算法分类及其具体算法:一、监督学习算法监督学习算法使用标记(即已知结果)的训练数据来训练模型,以便对新数据进行预测。线性回归:用于建立连续变量之间的关系,通过拟合一条直线或超平面来预测新数据的输出值。逻辑回归:虽然名称中包含“回归”,但实际上是用于分类问题,特别是二分类问题。通过将线性回归模
- 机器学习——逻辑回归
wsdswzj
机器学习逻辑回归人工智能
目录一、逻辑回归1.1、模型原理1.2、损失函数二、实例2.1、定义sigmoid函数2.2、数据集2.3、梯度上升算法2.4、预测函数2.5、绘画函数三、代码运行结果:四、总结优点:缺点:一、逻辑回归逻辑回归是一种广义的线性回归分析模型,用于解决二分类或多分类问题。逻辑回归模型,尽管名字中包含“回归”二字,实际上是一种分类方法,特别是用于处理二分类问题。它通过将线性回归的结果通过某种函数映射到(
- SAX解析xml文件
小猪猪08
xml
1.创建SAXParserFactory实例
2.通过SAXParserFactory对象获取SAXParser实例
3.创建一个类SAXParserHander继续DefaultHandler,并且实例化这个类
4.SAXParser实例的parse来获取文件
public static void main(String[] args) {
//
- 为什么mysql里的ibdata1文件不断的增长?
brotherlamp
linuxlinux运维linux资料linux视频linux运维自学
我们在 Percona 支持栏目经常收到关于 MySQL 的 ibdata1 文件的这个问题。
当监控服务器发送一个关于 MySQL 服务器存储的报警时,恐慌就开始了 —— 就是说磁盘快要满了。
一番调查后你意识到大多数地盘空间被 InnoDB 的共享表空间 ibdata1 使用。而你已经启用了 innodbfileper_table,所以问题是:
ibdata1存了什么?
当你启用了 i
- Quartz-quartz.properties配置
eksliang
quartz
其实Quartz JAR文件的org.quartz包下就包含了一个quartz.properties属性配置文件并提供了默认设置。如果需要调整默认配置,可以在类路径下建立一个新的quartz.properties,它将自动被Quartz加载并覆盖默认的设置。
下面是这些默认值的解释
#-----集群的配置
org.quartz.scheduler.instanceName =
- informatica session的使用
18289753290
workflowsessionlogInformatica
如果希望workflow存储最近20次的log,在session里的Config Object设置,log options做配置,save session log :sessions run ;savesessio log for these runs:20
session下面的source 里面有个tracing
- Scrapy抓取网页时出现CRC check failed 0x471e6e9a != 0x7c07b839L的错误
酷的飞上天空
scrapy
Scrapy版本0.14.4
出现问题现象:
ERROR: Error downloading <GET http://xxxxx CRC check failed
解决方法
1.设置网络请求时的header中的属性'Accept-Encoding': '*;q=0'
明确表示不支持任何形式的压缩格式,避免程序的解压
- java Swing小集锦
永夜-极光
java swing
1.关闭窗体弹出确认对话框
1.1 this.setDefaultCloseOperation (JFrame.DO_NOTHING_ON_CLOSE);
1.2
this.addWindowListener (
new WindowAdapter () {
public void windo
- 强制删除.svn文件夹
随便小屋
java
在windows上,从别处复制的项目中可能带有.svn文件夹,手动删除太麻烦,并且每个文件夹下都有。所以写了个程序进行删除。因为.svn文件夹在windows上是只读的,所以用File中的delete()和deleteOnExist()方法都不能将其删除,所以只能采用windows命令方式进行删除
- GET和POST有什么区别?及为什么网上的多数答案都是错的。
aijuans
get post
如果有人问你,GET和POST,有什么区别?你会如何回答? 我的经历
前几天有人问我这个问题。我说GET是用于获取数据的,POST,一般用于将数据发给服务器之用。
这个答案好像并不是他想要的。于是他继续追问有没有别的区别?我说这就是个名字而已,如果服务器支持,他完全可以把G
- 谈谈新浪微博背后的那些算法
aoyouzi
谈谈新浪微博背后的那些算法
本文对微博中常见的问题的对应算法进行了简单的介绍,在实际应用中的算法比介绍的要复杂的多。当然,本文覆盖的主题并不全,比如好友推荐、热点跟踪等就没有涉及到。但古人云“窥一斑而见全豹”,希望本文的介绍能帮助大家更好的理解微博这样的社交网络应用。
微博是一个很多人都在用的社交应用。天天刷微博的人每天都会进行着这样几个操作:原创、转发、回复、阅读、关注、@等。其中,前四个是针对短博文,最后的关注和@则针
- Connection reset 连接被重置的解决方法
百合不是茶
java字符流连接被重置
流是java的核心部分,,昨天在做android服务器连接服务器的时候出了问题,就将代码放到java中执行,结果还是一样连接被重置
被重置的代码如下;
客户端代码;
package 通信软件服务器;
import java.io.BufferedWriter;
import java.io.OutputStream;
import java.io.O
- web.xml配置详解之filter
bijian1013
javaweb.xmlfilter
一.定义
<filter>
<filter-name>encodingfilter</filter-name>
<filter-class>com.my.app.EncodingFilter</filter-class>
<init-param>
<param-name>encoding<
- Heritrix
Bill_chen
多线程xml算法制造配置管理
作为纯Java语言开发的、功能强大的网络爬虫Heritrix,其功能极其强大,且扩展性良好,深受热爱搜索技术的盆友们的喜爱,但它配置较为复杂,且源码不好理解,最近又使劲看了下,结合自己的学习和理解,跟大家分享Heritrix的点点滴滴。
Heritrix的下载(http://sourceforge.net/projects/archive-crawler/)安装、配置,就不罗嗦了,可以自己找找资
- 【Zookeeper】FAQ
bit1129
zookeeper
1.脱离IDE,运行简单的Java客户端程序
#ZkClient是简单的Zookeeper~$ java -cp "./:zookeeper-3.4.6.jar:./lib/*" ZKClient
1. Zookeeper是的Watcher回调是同步操作,需要添加异步处理的代码
2. 如果Zookeeper集群跨越多个机房,那么Leader/
- The user specified as a definer ('aaa'@'localhost') does not exist
白糖_
localhost
今天遇到一个客户BUG,当前的jdbc连接用户是root,然后部分删除操作都会报下面这个错误:The user specified as a definer ('aaa'@'localhost') does not exist
最后找原因发现删除操作做了触发器,而触发器里面有这样一句
/*!50017 DEFINER = ''aaa@'localhost' */
原来最初
- javascript中showModelDialog刷新父页面
bozch
JavaScript刷新父页面showModalDialog
在页面中使用showModalDialog打开模式子页面窗口的时候,如果想在子页面中操作父页面中的某个节点,可以通过如下的进行:
window.showModalDialog('url',self,‘status...’); // 首先中间参数使用self
在子页面使用w
- 编程之美-买书折扣
bylijinnan
编程之美
import java.util.Arrays;
public class BookDiscount {
/**编程之美 买书折扣
书上的贪心算法的分析很有意思,我看了半天看不懂,结果作者说,贪心算法在这个问题上是不适用的。。
下面用动态规划实现。
哈利波特这本书一共有五卷,每卷都是8欧元,如果读者一次购买不同的两卷可扣除5%的折扣,三卷10%,四卷20%,五卷
- 关于struts2.3.4项目跨站执行脚本以及远程执行漏洞修复概要
chenbowen00
strutsWEB安全
因为近期负责的几个银行系统软件,需要交付客户,因此客户专门请了安全公司对系统进行了安全评测,结果发现了诸如跨站执行脚本,远程执行漏洞以及弱口令等问题。
下面记录下本次解决的过程以便后续
1、首先从最简单的开始处理,服务器的弱口令问题,首先根据安全工具提供的测试描述中发现应用服务器中存在一个匿名用户,默认是不需要密码的,经过分析发现服务器使用了FTP协议,
而使用ftp协议默认会产生一个匿名用
- [电力与暖气]煤炭燃烧与电力加温
comsci
在宇宙中,用贝塔射线观测地球某个部分,看上去,好像一个个马蜂窝,又像珊瑚礁一样,原来是某个国家的采煤区.....
不过,这个采煤区的煤炭看来是要用完了.....那么依赖将起燃烧并取暖的城市,在极度严寒的季节中...该怎么办呢?
&nbs
- oracle O7_DICTIONARY_ACCESSIBILITY参数
daizj
oracle
O7_DICTIONARY_ACCESSIBILITY参数控制对数据字典的访问.设置为true,如果用户被授予了如select any table等any table权限,用户即使不是dba或sysdba用户也可以访问数据字典.在9i及以上版本默认为false,8i及以前版本默认为true.如果设置为true就可能会带来安全上的一些问题.这也就为什么O7_DICTIONARY_ACCESSIBIL
- 比较全面的MySQL优化参考
dengkane
mysql
本文整理了一些MySQL的通用优化方法,做个简单的总结分享,旨在帮助那些没有专职MySQL DBA的企业做好基本的优化工作,至于具体的SQL优化,大部分通过加适当的索引即可达到效果,更复杂的就需要具体分析了,可以参考本站的一些优化案例或者联系我,下方有我的联系方式。这是上篇。
1、硬件层相关优化
1.1、CPU相关
在服务器的BIOS设置中,可
- C语言homework2,有一个逆序打印数字的小算法
dcj3sjt126com
c
#h1#
0、完成课堂例子
1、将一个四位数逆序打印
1234 ==> 4321
实现方法一:
# include <stdio.h>
int main(void)
{
int i = 1234;
int one = i%10;
int two = i / 10 % 10;
int three = i / 100 % 10;
- apacheBench对网站进行压力测试
dcj3sjt126com
apachebench
ab 的全称是 ApacheBench , 是 Apache 附带的一个小工具 , 专门用于 HTTP Server 的 benchmark testing , 可以同时模拟多个并发请求。前段时间看到公司的开发人员也在用它作一些测试,看起来也不错,很简单,也很容易使用,所以今天花一点时间看了一下。
通过下面的一个简单的例子和注释,相信大家可以更容易理解这个工具的使用。
- 2种办法让HashMap线程安全
flyfoxs
javajdkjni
多线程之--2种办法让HashMap线程安全
多线程之--synchronized 和reentrantlock的优缺点
多线程之--2种JAVA乐观锁的比较( NonfairSync VS. FairSync)
HashMap不是线程安全的,往往在写程序时需要通过一些方法来回避.其实JDK原生的提供了2种方法让HashMap支持线程安全.
- Spring Security(04)——认证简介
234390216
Spring Security认证过程
认证简介
目录
1.1 认证过程
1.2 Web应用的认证过程
1.2.1 ExceptionTranslationFilter
1.2.2 在request之间共享SecurityContext
1
- Java 位运算
Javahuhui
java位运算
// 左移( << ) 低位补0
// 0000 0000 0000 0000 0000 0000 0000 0110 然后左移2位后,低位补0:
// 0000 0000 0000 0000 0000 0000 0001 1000
System.out.println(6 << 2);// 运行结果是24
// 右移( >> ) 高位补"
- mysql免安装版配置
ldzyz007
mysql
1、my-small.ini是为了小型数据库而设计的。不应该把这个模型用于含有一些常用项目的数据库。
2、my-medium.ini是为中等规模的数据库而设计的。如果你正在企业中使用RHEL,可能会比这个操作系统的最小RAM需求(256MB)明显多得多的物理内存。由此可见,如果有那么多RAM内存可以使用,自然可以在同一台机器上运行其它服务。
3、my-large.ini是为专用于一个SQL数据
- MFC和ado数据库使用时遇到的问题
你不认识的休道人
sqlC++mfc
===================================================================
第一个
===================================================================
try{
CString sql;
sql.Format("select * from p
- 表单重复提交Double Submits
rensanning
double
可能发生的场景:
*多次点击提交按钮
*刷新页面
*点击浏览器回退按钮
*直接访问收藏夹中的地址
*重复发送HTTP请求(Ajax)
(1)点击按钮后disable该按钮一会儿,这样能避免急躁的用户频繁点击按钮。
这种方法确实有些粗暴,友好一点的可以把按钮的文字变一下做个提示,比如Bootstrap的做法:
http://getbootstrap.co
- Java String 十大常见问题
tomcat_oracle
java正则表达式
1.字符串比较,使用“==”还是equals()? "=="判断两个引用的是不是同一个内存地址(同一个物理对象)。 equals()判断两个字符串的值是否相等。 除非你想判断两个string引用是否同一个对象,否则应该总是使用equals()方法。 如果你了解字符串的驻留(String Interning)则会更好地理解这个问题。
- SpringMVC 登陆拦截器实现登陆控制
xp9802
springMVC
思路,先登陆后,将登陆信息存储在session中,然后通过拦截器,对系统中的页面和资源进行访问拦截,同时对于登陆本身相关的页面和资源不拦截。
实现方法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23