距离Lec10更新已经过去三个半月了,漫长的考试与寒假……囧!今天终于鼓起勇气继续写下去,正好这学期有《统计学习方法》课程,结合着回顾一下。
按照惯例,开头是对上一节做出总结,由于时间久远,就算了……吧。
不过还是有一点其他东西想讲一讲。上周刚刚上了第一节统计学习方法课,基本是在宏观上介绍概念,很多名词和基石课叫法不一样,听起来怪怪的,但思想基本一样,有时候一下子联想不到基石中讲过的具体的知识点,所以也又想着再回来回顾一下。
碰巧,去年总结的最后一个Lec讲了LogReg,里面也提出来另一种err measure:likelihood。而统计学习方法中是把它与0/1 err、square err并列列出的,没有解释,命名为:对数损失函数or对数似然函数。当时看到的时候一下子就懵了,想不起具体是什么情况下出现的这个了,今天回顾才一下子想起来。现在只想说,难怪都说国内的教材看不得啊!列一个式子在那摆着,告诉别人叫什么,看的人如果之前没有接触过,根本理解不到其中的精髓呀!无论对错,就是小感慨一下!其实老师上课的时候讲概念还是挺严谨生动的,举了很多例子,但是不知道如果我之前没有上这门课听起来会是什么感觉?我猜是一头雾水,只是被灌输了一堆概念而不得其真意吧~!
下面回到正题,囧………………
Lec11: Linear Models for Classification
这节主要回顾三个线性模型,并对比讲解之间的联系。还会进一步介绍如何实现多分类
1、三个线性模型
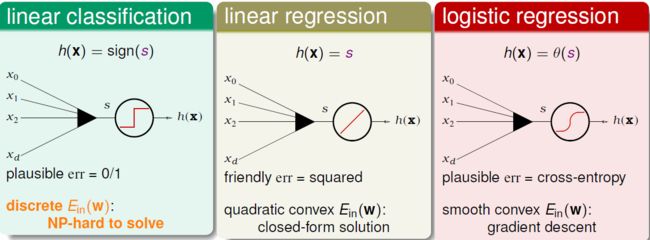
先回顾一下三个线性模型:线性分类,线性回归,逻辑回归,它们的共同点是都要计算一个score。既然它们这么像,而且线性回归和逻辑回归的优化似乎很容易计算,那么是不是可以用回归help分类呢?
先再回顾一下各自的error function,这里如果用作二元分类,则y取值为{-1,1},进一步将err都整理成 ys 形式。ys有其物理意义,y代表正确性,s代表score,乘积>0则正确,<0则错误。
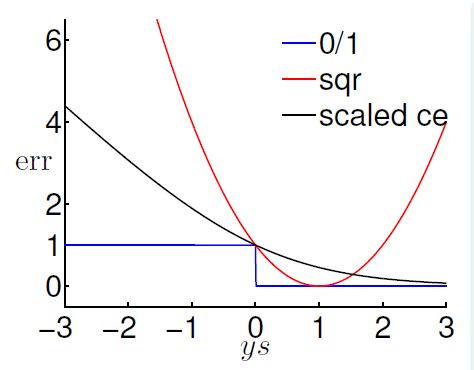
这三个err函数画图,发现
至此,再在ce err上动点手脚,scale一下,变ln为log2:
这样三条线关系如下,可以看出,sqr小的时候那么0/1也会小;scaled ce 与 0/1 相切;这两个线都在0/1err的上面,恩,这是用回归做分类的关键!upper bound!
使用upper bound在图上看很直接,理论上也很好理解,就是最小化0/1 err的上限,那么0/1 err也会小,所以可以用回归来做分类,算法为:
使用线性回归和逻辑回归的好处是优化简单,弊端是loose bound:
通常实际中,使用线性回归计算出来的w做为初始值w0,然后再进行PLA、pocket、逻辑回归;
此外,通常逻辑回归 prefer “pocket”,其实它们在优化过程中每一步的工作差不多……
2、Iterative Optimization方案 & 随机梯度下降(SGD)
前面已经介绍过PLA和梯度下降,都是迭代优化方法。
在PLA种,每一轮只选一个错误点更新w,复杂度是 O(1);而在LogReg的梯度下降方法中, 每一轮更新要把每一个点都要计算进去,复杂度是O(N);那么在梯度下降方法中,能不能做到每一轮更新的复杂度是O(1)呢?可以的:
回顾一下梯度下降中的迭代式子:
目标:计算direction时只使用一个点,而不是全部的(x,y)
技巧:把 ∑部分看做是期望,用随机选取一个点(xn,yn)计算的梯度取代梯度的期望值,称为随机梯度。
也可以把随机梯度看做是 true gradient + noise gradient,随机梯度下降法如下。其实在经过足够多步以后,随机梯度的平均和真实梯度的平均是接近的 ,这个类似随机抽样。这样会使计算简单高效,尤其是在data很大 以及 online learning(data是一个一个的in)。但这种方法会不太稳定,尤其是当η较大时,很可能会“一步踏空”。
将SGD用在LogReg上面:
这个式子更新跟(yx)有关,是和什么相似呢?PLA!回顾again:
PLA是用前面部分控制有错的时候更新,没错的时候不更新。这样,其实SGD LogReg就可以看成是soft PLA,这时不是有错更新,而是错的多一点就多更新一点,错的少一点就少更新一点。反过来看,如果WtXn很大,η=1时,其实θ()要么接近0要么接近1,PLA ≈ SGD 。虽然如此,但是在实际应用中要注意两点:一是SGD何时停下?梯度等于0吗?不,否则省的计算就白省了,一般 t 够大就停止;而是η的取值,经验上0.1126是不错的选择。后面会介绍取值选择方法。
3、多分类
下面介绍多类别分类,从是非题到选择题的转变,从二元分类延伸到多类别……
这里介绍两种思路:one vs all 和 one vs one。
第一种one vs all(OVA):
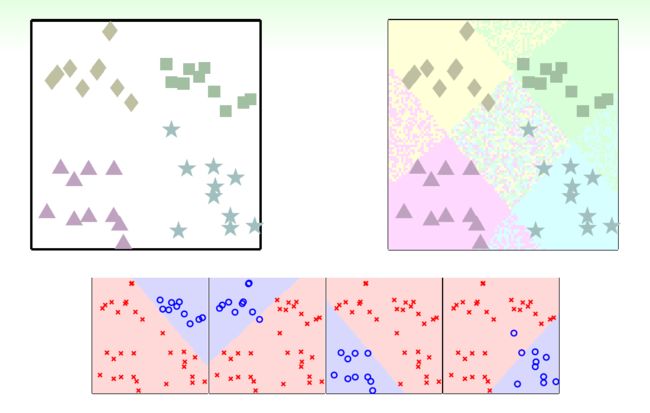
每次还是做二元分类,比如先把方块和其他分开;再把菱形和其他分开……最后组合四个分类器,得到下图。可以看出其实会有两个问题:有些区域重叠,分类器会互相争抢;有些区域未被分类器覆盖。分类器总是会犯错的…………
那么怎么办呢?softly classification,使用LogReg计算可能性,选择可能性最大的类别作为分类结果!实际上,score越大可能性也就越大,直接比较score就可以了。组合起来:
这里是拿LogReg做例子,实际上只要是输出值可以比大小的算法都可以用在OVA上面。
虽然这种方法是最简单基本的多分类方法,效率很高,但是数据会经常unbalanced:比如 o 很少,而 × 非常多的时候,如果把所有data都分为 × 就可以做的很好。下面方法可以解决这个问题……
第二种 one vs one(OVO ):
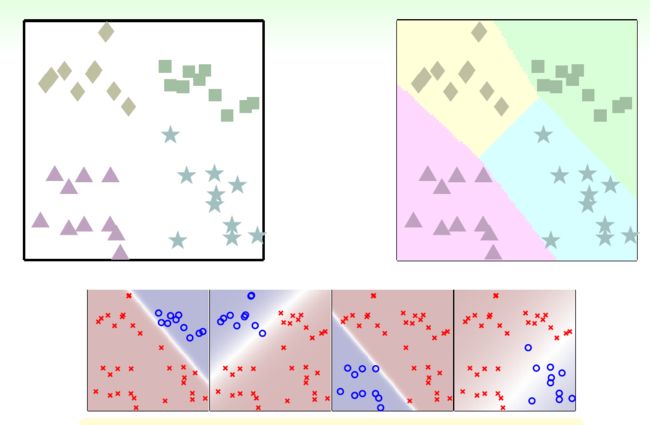
方块跟菱形分类,再方块跟三角形分类…………有4个分类,4选2,共有6种分类问题。最后如何根据6个分类器决定最后的结果呢?4个类别打了6场循环赛,赢得最多的类别胜出。如:前三个分类器都把某个data分类为方块,第四个分为菱形,第五个分为星星,第六个说比较像星星,最后方块胜出!
这个方法也很有效率(每一轮的问题规模较小),更稳定也可以跟任何的二元分类算法搭配。缺点是O(k平方),预测时间长,空间复杂度大,需要训练更多的分类器。
OVO也是很简单的多分类算法,尤其是类别不是很多的时候还是很好用的。
(还没从假期综合症中清醒过来,写的不细致,好在问题比较简单……就这样了)