决策树
通过构造决策树来区分鸢尾花
须知概念
信息熵 -- 表示信息混乱程度,信息越杂乱,熵值越大,信息越有序,熵值越小
信息增益 -- 在某操作前后(比如这里的划分数据集,信息熵变化称为信息增益。若熵值减小,表示数据越有序。
信息增益率 -- 信息增益/影响的数据集的大小。表示变化率。
Package
import numpy as np
from utils import calc_accuracy_class
from utils import fl_score
from utils import nomalize
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn import tree
import pydotplus
import pandas as pd
导入数据集
X,y = datasets.load_iris(return_X_y=True)
y = y.reshape(-1,1)
#将数据分为训练集和测试集
train_X,test_X,train_y,test_y = train_test_split(X,y,test_size = 0.20,random_state = 1)
print(f"train_X的大小为:{train_X.shape}")
print(f"tain_y的大小为:{train_y.shape}")
print(f"test_X的大小为:{test_X.shape}")
print(f"test_y的大小为:{test_y.shape}")
train_X的大小为:(120, 4)
tain_y的大小为:(120, 1)
test_X的大小为:(30, 4)
test_y的大小为:(30, 1)
train_X[0:10]
array([[6.1, 3. , 4.6, 1.4],
[7.7, 3. , 6.1, 2.3],
[5.6, 2.5, 3.9, 1.1],
[6.4, 2.8, 5.6, 2.1],
[5.8, 2.8, 5.1, 2.4],
[5.3, 3.7, 1.5, 0.2],
[5.5, 2.3, 4. , 1.3],
[5.2, 3.4, 1.4, 0.2],
[6.5, 2.8, 4.6, 1.5],
[6.7, 2.5, 5.8, 1.8]])
使用sklearn的库看看效果
tree_classifier = tree.DecisionTreeClassifier()
tree_classifier.fit(train_X,train_y)
pred_y = tree_classifier.predict(train_X)
currect = np.sum(np.squeeze(pred_y) == np.squeeze(train_y))/train_y.shape[0]
print(f"训练集的准确率为:{currect}")
pred_y = tree_classifier.predict(test_X)
currect = np.sum(np.squeeze(pred_y) == np.squeeze(test_y))/test_y.shape[0]
print(f"测试集的准确率为:{currect}")
训练集的准确率为:1.0
测试集的准确率为:0.9666666666666667
dot_data = tree.export_graphviz(tree_classifier,out_file=None)
graph = pydotplus.graph_from_dot_data(dot_data)
graph.write_pdf("iris.pdf")
True
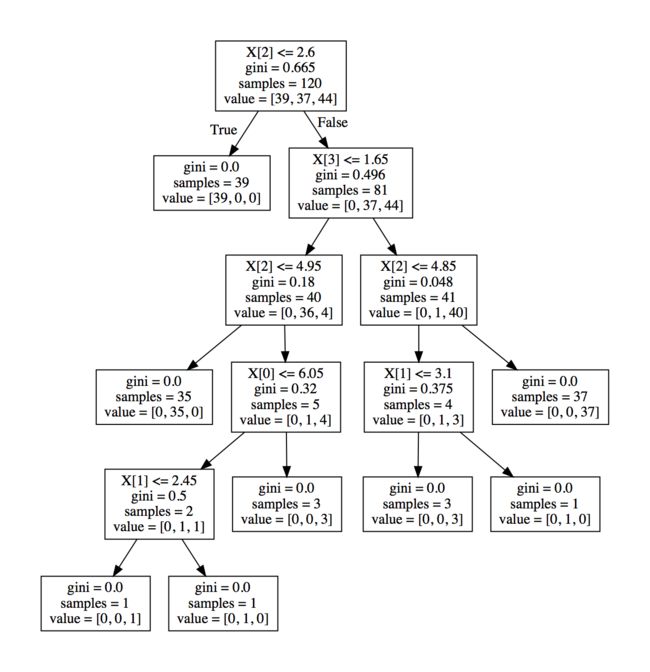
我们导出了树的pdf,如下所示:
接下来,我们来自己实现一下
代码实现
信息熵计算
假设有K个分类,表示表示第k个分类的概率,。
则信息熵为:
而根据大数定理,当数据达到一定量的时候,我们可以用频率来表示概率。
所以可通过频率来算出P(k)
def compute_entropy(train_y):
'''
给定数据集,求出信息熵
'''
train_y = train_y.reshape(-1,)
classes = set(train_y)
m = train_y.shape[0]
entropy = 0
for c in classes:
n_c = np.sum(train_y.reshape(-1,) == c) #c类的个数
p_c = n_c/m
entropy = entropy - (p_c)*np.log(p_c)
return entropy
根据最好的特征及分裂条件拆分数据集
我们的特征值是多个散列的浮点数集合,由sklearn库得出的树图可知,它将散列点按照某个值(均值或中间值等)划分为两列。
这里我们使用均值划分
def split_data_set(X,y,feature_index):
'''
Function:
根据分裂点及条件进行分裂
Arguments:
X -- shape is (m,n)
y -- shape is (m,1)
feature_Index -- 一个数值,表示特征的索引
Return:
ret_X -- 一个list,包含分裂后的两组X数据
ret_y -- 一个list,包含分裂后的两组y数据
'''
m = X.shape[0]
sub_features = X[:,feature_index]
# temp = np.sort(sub_features)
# mid_idx = int(len(temp)/2)
# mid_num = temp[mid_idx]
# con_value = mid_num
con_value = np.sum(sub_features)/m #均值作为分裂点
subset_index1 = np.where(sub_features <= con_value)
subset_index2 = np.where(sub_features > con_value)
subset_X1 = X[subset_index1]
subset_X2 = X[subset_index2]
subset_y1 = y[subset_index1]
subset_y2 = y[subset_index2]
return subset_X1,subset_X2,subset_y1,subset_y2,con_value
选取最好的特征进行分裂
当有N个特征的时候,如何选择分裂特征呢?
选择信息熵下降最快的那个特征作为分裂特征。即信息增益或信息增益率最大的那个。
两个所对应的算法分别为:IC3算法,C4.5算法
首先,我们是希望我们构建的决策树越矮越好,如果能够少几次分裂就能够分好类的,又何必多分几次呢
所以,也就是分裂次数越少越好。要做到分裂次数越少越好,那就最好是每一次分裂都能够最大程度的将数据区分开来。
这个最大区分开来的意思,就是每次分裂,每个子分类都越来越“纯”,即每个子分类的熵越低越好。
那么基于此,最好的特征就是能够最快降低信息熵的那个。
def choose_best_feature(X,y):
'''
Function:
选择最好的分裂特征
Arguments:
X -- shape is (m,n)
y -- shape is (m,1)
Return:
best_feature_index -- 好分裂特征的索引值
best_split_conval -- 分裂的条件值
'''
#先计算基础熵
base_entorpy = compute_entropy(y)
m,n_x = X.shape
gain = 0
best_feature_index = 0
best_split_conval = 0
for index in range(n_x):
_,_,subset_y1,subset_y2,con_value = split_data_set(X,y,index)
#计算两个的信息熵
m1 =subset_y1.shape[0]
m2 = subset_y2.shape[0]
entropy1 = compute_entropy(subset_y1)
entropy2 = compute_entropy(subset_y2)
sum_entropy =(m1/m) *entropy1+(m2/m)*entropy2
#计算信息增益
sub_gain = base_entorpy-sum_entropy
#print(f"{index}的信息增益为:{sub_gain}")
if sub_gain > gain:
gain = sub_gain
best_feature_index = index
best_split_conval = con_value
#print(f"best gain is {gain},index is {best_feature_index}")
return best_feature_index,best_split_conval
构建决策树
#生成一个子节点
def create_node(X,y,node_no,node_index,index, classes,cond_value=None,parent_cond_branch=None):
'''
Function:
根据数据生成一个子节点
Arguments:
X -- 特征,shape is (m,n)
y -- label,shape is (m,1)
node_no -- json点编号,标识是第几层节点
index -- 特征索引
classes -- 分类类别
Return:
node -- a list of dict,include:
node_no -- 节点编号
index:特征索引
cond_value: 条件值 如 5.5 若不再分裂,则为None
parent_cond_branch -- 父节点的条件分支 在这用0表示False分支,1 表示True分支。没有,则为None
samples -- 样本总数
values -- a list,记录每个分类的样本个数 ,如[47,49,58]
# is_need_split -- 是否需要继续分裂 0:继续分裂; 1:停止分裂
'''
node = {}
node["node_no"] = node_no
node["node_index"] = node_index
node["index"] = index
node["cond_value"] = cond_value
node["parent_cond_branch"] = parent_cond_branch
node["samples"] = X.shape[0]
values = []
y_ = y.reshape(-1,)
for sub_y in classes:
count = np.sum(y_ == sub_y)
values.append(count)
node["values"] = values
return node
def create_tree(node_list,classes,mytree):
'''
Function:
构建决策树
Arguments:
node_list -- 节点列表,列表信息包含多个元组,每个元组有(X,y,node_no,parent_cond_branch)
y -- label,shape is (m,1)
Return:
mytree -- a list of dict,include:
node_no -- 每一层的节点编号
node_index -- 节点层次索引
index:特征索引
cond_value: 条件值 如 5.5
parent_cond_branch -- 父节点的条件分支 在这用0表示False分支,1 表示True分支
samples -- 样本总数
values -- a list,记录每个分类的样本个数 ,如[47,49,58]
'''
split_list = []
sub_node_list = []
for sub_node in node_list:
X,y,node_index,parent_cond_branch,node_no = sub_node
# 如果只有一个类别,则不再分裂
if len(set(y.reshape(-1,))) == 1 or (y.shape[0] < 5) :
node = create_node(X,y,node_no,node_index,index = None,parent_cond_branch=parent_cond_branch,classes=classes)
key = str(node_index)+"-"+str(node_no)
mytree[key] = node
continue
best_feature_index,best_split_conval = choose_best_feature(X,y)
node = create_node(X,y,node_no,node_index,best_feature_index,classes,cond_value=best_split_conval,parent_cond_branch=parent_cond_branch)
key = str(node_index)+"-"+str(node_no)
mytree[key] = node
subset_X1,subset_X2,subset_y1,subset_y2,_ = split_data_set(X,y,best_feature_index)
next_index = node_index+1
#因为为二分裂,所以分裂的node_no为父node_no*2+parent_cond_branch
split_list.append((subset_X1,subset_y1,next_index,0,node_no*2+0))
split_list.append((subset_X2,subset_y2,next_index,1,node_no*2+1))
if(len(split_list) > 0):
create_tree(split_list,classes,mytree)
训练
def fit(train_X,train_y):
mytree = {}
classes = set(np.squeeze(train_y))
node_list = [(train_X,train_y,0,0,0)]
create_tree(node_list,classes,mytree)
return mytree,classes
mytree,classes = fit(train_X,train_y)
print(mytree)
{'0-0': {'node_no': 0, 'node_index': 0, 'index': 2, 'cond_value': 3.8100000000000005, 'parent_cond_branch': 0, 'samples': 120, 'values': [39, 37, 44]}, '1-0': {'node_no': 0, 'node_index': 1, 'index': 2, 'cond_value': 1.7804347826086957, 'parent_cond_branch': 0, 'samples': 46, 'values': [39, 7, 0]}, '1-1': {'node_no': 1, 'node_index': 1, 'index': 3, 'cond_value': 1.754054054054054, 'parent_cond_branch': 1, 'samples': 74, 'values': [0, 30, 44]}, '2-0': {'node_no': 0, 'node_index': 2, 'index': None, 'cond_value': None, 'parent_cond_branch': 0, 'samples': 38, 'values': [38, 0, 0]}, '2-1': {'node_no': 1, 'node_index': 2, 'index': 3, 'cond_value': 0.95, 'parent_cond_branch': 1, 'samples': 8, 'values': [1, 7, 0]}, '2-2': {'node_no': 2, 'node_index': 2, 'index': 3, 'cond_value': 1.3764705882352941, 'parent_cond_branch': 0, 'samples': 34, 'values': [0, 29, 5]}, '2-3': {'node_no': 3, 'node_index': 2, 'index': 1, 'cond_value': 3.0, 'parent_cond_branch': 1, 'samples': 40, 'values': [0, 1, 39]}, '3-2': {'node_no': 2, 'node_index': 3, 'index': None, 'cond_value': None, 'parent_cond_branch': 0, 'samples': 1, 'values': [1, 0, 0]}, '3-3': {'node_no': 3, 'node_index': 3, 'index': None, 'cond_value': None, 'parent_cond_branch': 1, 'samples': 7, 'values': [0, 7, 0]}, '3-4': {'node_no': 4, 'node_index': 3, 'index': None, 'cond_value': None, 'parent_cond_branch': 0, 'samples': 15, 'values': [0, 15, 0]}, '3-5': {'node_no': 5, 'node_index': 3, 'index': 2, 'cond_value': 4.7631578947368425, 'parent_cond_branch': 1, 'samples': 19, 'values': [0, 14, 5]}, '3-6': {'node_no': 6, 'node_index': 3, 'index': None, 'cond_value': None, 'parent_cond_branch': 0, 'samples': 26, 'values': [0, 0, 26]}, '3-7': {'node_no': 7, 'node_index': 3, 'index': 3, 'cond_value': 2.2285714285714286, 'parent_cond_branch': 1, 'samples': 14, 'values': [0, 1, 13]}, '4-10': {'node_no': 10, 'node_index': 4, 'index': 1, 'cond_value': 2.9, 'parent_cond_branch': 0, 'samples': 11, 'values': [0, 10, 1]}, '4-11': {'node_no': 11, 'node_index': 4, 'index': 2, 'cond_value': 5.1499999999999995, 'parent_cond_branch': 1, 'samples': 8, 'values': [0, 4, 4]}, '4-14': {'node_no': 14, 'node_index': 4, 'index': 0, 'cond_value': 6.683333333333334, 'parent_cond_branch': 0, 'samples': 6, 'values': [0, 1, 5]}, '4-15': {'node_no': 15, 'node_index': 4, 'index': None, 'cond_value': None, 'parent_cond_branch': 1, 'samples': 8, 'values': [0, 0, 8]}, '5-20': {'node_no': 20, 'node_index': 5, 'index': 3, 'cond_value': 1.5, 'parent_cond_branch': 0, 'samples': 5, 'values': [0, 4, 1]}, '5-21': {'node_no': 21, 'node_index': 5, 'index': None, 'cond_value': None, 'parent_cond_branch': 1, 'samples': 6, 'values': [0, 6, 0]}, '5-22': {'node_no': 22, 'node_index': 5, 'index': 2, 'cond_value': 4.966666666666666, 'parent_cond_branch': 0, 'samples': 6, 'values': [0, 4, 2]}, '5-23': {'node_no': 23, 'node_index': 5, 'index': None, 'cond_value': None, 'parent_cond_branch': 1, 'samples': 2, 'values': [0, 0, 2]}, '5-28': {'node_no': 28, 'node_index': 5, 'index': None, 'cond_value': None, 'parent_cond_branch': 0, 'samples': 3, 'values': [0, 1, 2]}, '5-29': {'node_no': 29, 'node_index': 5, 'index': None, 'cond_value': None, 'parent_cond_branch': 1, 'samples': 3, 'values': [0, 0, 3]}, '6-40': {'node_no': 40, 'node_index': 6, 'index': None, 'cond_value': None, 'parent_cond_branch': 0, 'samples': 4, 'values': [0, 4, 0]}, '6-41': {'node_no': 41, 'node_index': 6, 'index': None, 'cond_value': None, 'parent_cond_branch': 1, 'samples': 1, 'values': [0, 0, 1]}, '6-44': {'node_no': 44, 'node_index': 6, 'index': None, 'cond_value': None, 'parent_cond_branch': 0, 'samples': 3, 'values': [0, 3, 0]}, '6-45': {'node_no': 45, 'node_index': 6, 'index': None, 'cond_value': None, 'parent_cond_branch': 1, 'samples': 3, 'values': [0, 1, 2]}}
预测
def node_judge(node,X,mytree):
feature_indx = node["index"]
node_no = node["node_no"]
cond_value = node["cond_value"]
node_index = node["node_index"]
values = node["values"]
if feature_indx == None: #表示已经到最后的节点,执行预测
class_index = np.argmax(values)
return class_index
else:
feature_X = X[feature_indx]
next_node_index = node_index+1
next_parent_cond_branch = 0
if feature_X > cond_value:
next_parent_cond_branch = 1
next_key = str(next_node_index)+"-"+str(node_no*2+next_parent_cond_branch)
next_node = mytree[next_key]
return node_judge(next_node,X,mytree)
def predict(X,mytree,classes):
root = mytree["0-0"] #第一个根节点
pred_y = []
classes = list(classes)
for x in X:
class_index = node_judge(root,x,mytree)
pred_y.append(classes[class_index])
return np.array(pred_y)
pred_y = predict(train_X,mytree,classes)
acc = calc_accuracy_class(pred_y.T,train_y)
print("训练集的正确率为:"+str(acc))
pred_y = predict(test_X,mytree,classes)
acc = calc_accuracy_class(pred_y.T,test_y)
print("测试集的正确率为:"+str(acc))
训练集的正确率为:0.9833333333333333
测试集的正确率为:0.9666666666666667