《有理数加法》教研实录
小学阶段我们学过了正数及0的加法运算,步入中学后数系就扩张到了有理数范围内,从和学生一起感知整个数系的扩充过程、有理数的由来,到精确学习了什么是有理数、相反数、绝对值以及研究有理数的主要工具数轴。在前期的基础之上,接下来就会步入数的运算环节,这个是重点也是难点。运算法则不难,让学生总结归纳然后大量训练加以巩固即可,但这与传统教育没有任何的差别,最终孩子们只学会套路式的计算,不能从根本上理解有理数各种运算的本质,在思维上只有灌输,没有对孩子形成头脑冲击,所以前者是不可取的。
今天的课堂主要是探讨和推导有理数加法的算理和算法,如何借助生活场景或者数轴来演绎有理数加法的合理性,从而推导出算法。在课程设计之前,我尝试了用物体的矢量运动、温差的变化、以及海拔升降,以及购物中的收入和支出来搭建模型,甚至考虑过用正负电荷进行演绎。但在思路和逻辑上,都无法厘的很清楚。最终还是选择了学生更能理解的物体的矢量运动进行建立模型。
课前通过两道前测题对学生已有的有理数加法的元认知进行了一个检测。
前测1:
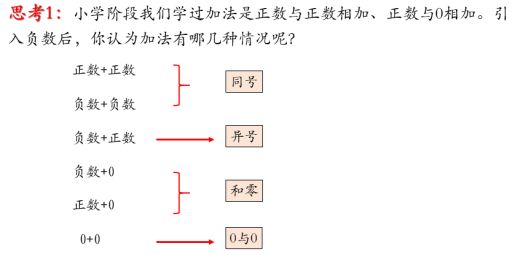
思考1:小学阶段我们学过加法是正数与正数相加、正数与0相加。引入负数后,你认为加法有哪几种情况呢?
前测2:
问题探究:一个物体做左右运动,我们规定向左为负,向右为正。
例如:向右运动5米记作+5m,向左运动5米记作-5m。
思考2:根据上述问题探究,分别对下列问题进行列式并计算结果。并运用数轴来验证你的计算结果是否合理。
1. 如果物体先向右运动5m ,再向右运动3m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
2. 如果物体先向左运动5m,再向左运动3m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
3. 如果物体先向左运动3m,再向右运动5m,那么两次运动的最后结果怎样?如何用算式表示?
4. 如果物体先向右运动3m,再向左运动5m,那么两次运动的数后结果怎样?如何用算式表示?
前测的结果很理想,在前期已学得的知识的基础上,大部分同学能通过利用数轴上点的运动得到正确的结果和列式。
课堂也主要是围绕这两个前测单展开;
板块一:围绕前测1中学生的问题入手,和学生一起讨论合理与否,合理原因何在?不合理,阐述你的观点。同学们积极参与推进了课堂的节奏,我们推倒了各种各样的回答:
课堂直接找茬并纠正了这些问题,最终达成一致性共识。归类如下:
此环节意图:让学生更加清晰的认识到有理数加法的几种情况,为更清楚探究有理数加法做准备。
板块二:围绕前测2中的问题展开,结合学生的回答,和学生讨论、纠错、探究、总结,课堂的高潮和烧脑也正是从此开始,本来好像一切都按部就班的进行着,孩子们积极参与,我也讲的如火朝天,借助数轴上代表数的点的运动来理解加法的运算原理,孩子接收的程度确实不错。
但干老师的一把火点燃了整个课堂,针对上图,干老师提出疑问;
1) 0是运动的起点还是正负数的临界点?
2)第一次运动的结果是-5可以看的出,但数轴上-3的点在哪里?
3)数轴的本质是用来表示数的,在此数轴上该如何表示-3的点?
4)怎么才可以更加直观的在数轴上表述出-5+(-3)呢?
学生开始争相表达自己的观点,陈老师、何老师也参与到了课堂,关于疑问提出自己观点,我的场瞬间被抢走了,被孤立起来了,只有站在旁边看好戏,以干老师的话说就是完美诠释什么叫喧宾夺主,其实我心里美滋滋的,争的越凶越好。
问题的争论好像有了结论,孩子们一致认为通过点的运动就非常直观的展示了,干老师又问:“哪么2—(—3)呢?你又该如何解释?如何通过运动来表示?”孩子们瞬间蒙了,是的,该怎么解释呢?孩子们开始讨论,有的孩子说:“老师,负负本来就得正,还用证明吗?”可是“负负得正”到底是为什么呢?
总算到我登场了,也该到总结陈述的时候了,再怎么激烈的课堂,节奏还是要有的,不然就丧失了本节课的核心了。到底为什么“负负会得正”?我们该用怎样的生活例子或如何运用数轴才能更好的诠释加法的运算呢?这个问题留给孩子们课下思考,这是一个挑战,也是一个不断思维的过程。
板块三总结
通过前边的模型建构和激烈讨论,总结归纳出有理数的运算法则:
(1) 同号两数相加,取相同的符号,并把绝对值相加;
(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;
(3)互为相反数的两个数相加得0;
(4) 一个数同0相加,仍得这个数。
板块四精确练习
初中阶段对孩子们的各项要求都提高了,要训练孩子们做题的规范性以及严谨的数学思维和逻辑思维。训练某种方法,按照要求的方法进行训练,以达到做题自动化。
【课后教研】
教研主题1:如何运用数轴更加合理的来解释有理数各种运算的算理,并且具有统一性。
干老师指出,用方向来解释有理数加法运算的原理是可以的,但是太过于牵强,而且会给学生造成后遗症,因为并不能用此解释模型将有理数的各种运算一以贯之,数系扩充到有理数范围内,它的运算算理解释模型应该是统一的,而不是每一种运算有一种不同的解释模型出来,这样是不合理的。首先我们要清楚数轴的本质是什么?我们要明白数轴的绝对含义是什么?数轴仅仅用来表示数,我们不能把数轴当做走的图示,这是不同的概念。例如,数轴上的“5”,“3”这样的点,仅仅表示从零点开始的数而已。
对数轴而言,严格来说,每一个数轴上的点都表示从零点开始的线段长度。我们最后求的是5和3的和是多少就表示0-5和0-3两段长度的和是多少?而3-5的时候就已经在颠倒了,实际上按照数学逻辑来说,第一个数据是+5和+3,8只是表示累加的结果,我们题目中并未出现8,它只是累加的结果。我们的数轴其实就像一个尺子,我们要做加减法时候,每一个数都应该在数轴上列出来,而不应该我们自己给它们赋予不同的含义。
那么我们理数的减法又怎么在数轴上进行表示呢?其实原理是一样的,比如我们画一个图,+8和+6进行相加,在数轴上画出他们的位置,把它们到原点距离相加就表示8+6的过程,必定是叠加。但如果一个是正数,一个是负数的话,由于一个在原点左侧,一个在原点右侧,它们相加表示到原点的距离和方向不一样,就会相互抵消。距离远的就更加大,取它的符号,长度会抵消较小的那个数的长度。
结论:以2—(—3)为例,首先我们应该在数轴上准确的找到表示2和-3的点,然后根据数的性质进行运算,图示如下:
整个过程通过动图演示,让学生更加直观的感受为什么“负负得正”。同理,通过这样,有理数加法、乘法、除法都可以类似的方法进行解释,而且所有运算算理研究的方法都是一以贯之的,学生的理解也会越来越深。