余弦距离与欧几里德距离都是常用的距离度量方式。
关于两个向量之间求距离的能找到很多的参考材料,这里就不再赘述了。
在项目中用到了两个矩阵的多行向量需要计算两两之间的距离,就在这里做一个分享。
一 余弦距离
- 直接上代码啦:
def cosine_distance(matrix1,matrix2):
matrix1_matrix2 = np.dot(matrix1, matrix2.transpose())
matrix1_norm = np.sqrt(np.multiply(matrix1, matrix1).sum(axis=1))
matrix1_norm = matrix1_norm[:, np.newaxis]
matrix2_norm = np.sqrt(np.multiply(matrix2, matrix2).sum(axis=1))
matrix2_norm = matrix2_norm[:, np.newaxis]
cosine_distance = np.divide(matrix1_matrix2, np.dot(matrix1_norm, matrix2_norm.transpose()))
return cosine_distance
- 运行结果验证:
matrix1=np.array([[1,1],[1,2]])
matrix2=np.array([[2,1],[2,2],[2,3]])
cosine_dis=cosine_distance(matrix1,matrix2)
print (cosine_dis)
-
结果:
~~
20190307更新
这个也有封装好的,只是之前没有发现(▽)
from sklearn.metrics.pairwise import cosine_similarity
cosine_dis2 = cosine_similarity(matrix1,matrix2)
- 验证:
from sklearn.metrics.pairwise import cosine_similarity
def cosine_distance(matrix1, matrix2):
matrix1_matrix2 = np.dot(matrix1, matrix2.transpose())
matrix1_norm = np.sqrt(np.multiply(matrix1, matrix1).sum(axis=1))
matrix1_norm = matrix1_norm[:, np.newaxis]
matrix2_norm = np.sqrt(np.multiply(matrix2, matrix2).sum(axis=1))
matrix2_norm = matrix2_norm[:, np.newaxis]
cosine_distance = np.divide(matrix1_matrix2, np.dot(matrix1_norm, matrix2_norm.transpose()))
return cosine_distance
matrix1=np.array([[1,1],[1,2]])
matrix2=np.array([[2,1],[2,2],[2,3]])
cosine_dis=cosine_distance(matrix1,matrix2)
print ('cosine_dis:',cosine_dis)
cosine_dis2 = cosine_similarity(matrix1,matrix2)
print('cosine_dis2:',cosine_dis2)
- 结果:
[[0.9486833 1. 0.98058068]
[0.8 0.9486833 0.99227788]]
[[0.9486833 1. 0.98058068]
[0.8 0.9486833 0.99227788]]
二 欧几里德距离
- 代码:
def EuclideanDistances(A, B):
BT = B.transpose()
vecProd = np.dot(A,BT)
SqA = A**2
sumSqA = np.matrix(np.sum(SqA, axis=1))
sumSqAEx = np.tile(sumSqA.transpose(), (1, vecProd.shape[1]))
SqB = B**2
sumSqB = np.sum(SqB, axis=1)
sumSqBEx = np.tile(sumSqB, (vecProd.shape[0], 1))
SqED = sumSqBEx + sumSqAEx - 2*vecProd
SqED[SqED<0]=0.0
ED = np.sqrt(SqED)
return ED
- 运行结果验证:
matrix1=np.array([[1,1],[1,2]])
matrix2=np.array([[2,1],[2,2],[2,3]])
Euclidean_dis=EuclideanDistances(matrix1,matrix2)
print (Euclidean_dis)
-
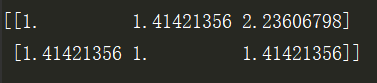
结果:
20190223更新~~~~~~~~
发现已经有封装好的函数了哈哈哈哈,顺便又验证了一下上面的代码:
from scipy.spatial.distance import cdist
dis = cdist(matrix1,matrix2,metric='euclidean')
- 验证代码
matrix1 = np.array([[1, 1], [1, 2]])
matrix2 = np.array([[2, 1], [2, 2], [2, 3]])
Euclidean_dis= EuclideanDistances(matrix1, matrix2)
print(Euclidean_dis)
from scipy.spatial.distance import cdist
dis = cdist(matrix1,matrix2,metric='euclidean')
print(dis)
print(Euclidean_dis==dis)
- 结果:
[[1. 1.41421356 2.23606798]
[1.41421356 1. 1.41421356]]
[[1. 1.41421356 2.23606798]
[1.41421356 1. 1.41421356]]
[[ True True True]
[ True True True]]
三 参考资料
- 余弦距离自己写的
- 欧几里德距离参考文章:求两个矩阵中向量的欧氏距离(python实现)
- https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.distance.cdist.html