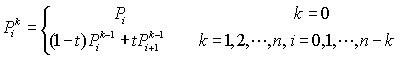APK下载地址
1.贝塞尔曲线
以下公式中:
B(t)为t时间下 点的坐标;
P0为起点,Pn为终点,Pi为控制点
一阶贝塞尔曲线(线段):
意义:由 P0 至 P1 的连续点, 描述的一条线段
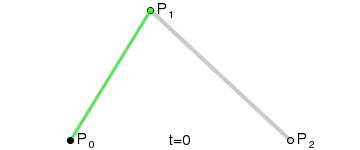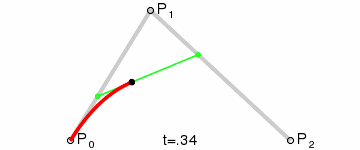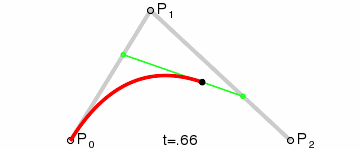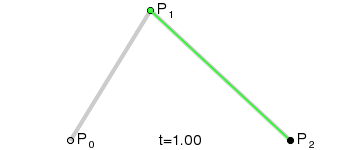
二阶贝塞尔曲线(抛物线):
原理:由 P0 至 P1 的连续点 Q0,描述一条线段。
由 P1 至 P2 的连续点 Q1,描述一条线段。 由 Q0 至 Q1 的连续点 B(t),描述一条二次贝塞尔曲线。 经验:P1-P0为曲线在P0处的切线。
三阶贝塞尔曲线:
通用公式:
高阶贝塞尔曲线:
4阶曲线:
5阶曲线:
1.1.生成贝塞尔曲线-迭代法
下面我们用代码来生成贝塞尔曲线,来展示如何贝塞尔曲线的生成原理:
package com.che.chechengwang.support.view.bezier;
import android.animation.FloatEvaluator;
import android.animation.ValueAnimator;
import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.Path;
import android.graphics.PointF;
import android.util.AttributeSet;
import android.view.View;
import android.view.animation.LinearInterpolator;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
import java.util.Random;
/**
* 生成贝塞尔曲线-迭代法
*
* 作者:余天然 on 16/6/14 下午2:10
*/
public class BezierGenerater1 extends View {
private Paint paint;
private int centerX, centerY;
private List points;
private FloatEvaluator evaluator;
private float fraction;
private Map colors;
private List destPoints;
public BezierGenerater1(Context context, AttributeSet attrs) {
super(context, attrs);
init();
}
private void init() {
paint = new Paint();
paint.setAntiAlias(true);
paint.setStyle(Paint.Style.STROKE);
evaluator = new FloatEvaluator();
startAnim();
}
//初始化数据点和控制点的位置
@Override
protected void onSizeChanged(int w, int h, int oldw, int oldh) {
super.onSizeChanged(w, h, oldw, oldh);
centerX = w / 2;
centerY = h / 2;
points = new ArrayList<>();
points.add(new PointF(centerX - 150, centerY));
points.add(new PointF(centerX - 50, centerY - 300));
points.add(new PointF(centerX + 50, centerY + 300));
points.add(new PointF(centerX + 150, centerY));
colors = new HashMap<>();
for (int i = 0; i < points.size(); i++) {
colors.put(i, getRanColor());
}
destPoints = new ArrayList<>();
destPoints.add(points.get(0));
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
//静态的
drawPoint(canvas, points, Color.BLACK);
drawLine(canvas, points, Color.GRAY);
//动态的
List subData = getSubData(points, fraction);
drawData(canvas, subData, fraction);
}
// 绘制数据点
private void drawPoint(Canvas canvas, List data, int color) {
paint.setColor(color);
paint.setStrokeWidth(20);
for (int i = 0; i < data.size(); i++) {
PointF pointF = data.get(i);
canvas.drawPoint(pointF.x, pointF.y, paint);
}
}
//绘制基准线
private void drawLine(Canvas canvas, List data, int color) {
paint.setColor(color);
paint.setStrokeWidth(4);
for (int i = 0; i < data.size() - 1; i++) {
PointF start = data.get(i);
PointF end = data.get(i + 1);
canvas.drawLine(start.x, start.y, end.x, end.y, paint);
}
}
//绘制路径
private void drawPath(Canvas canvas, List data) {
Path path = new Path();
PointF start = data.get(0);
path.moveTo(start.x, start.y);
for (int i = 1; i < data.size() - 1; i++) {
PointF point = data.get(i);
path.lineTo(point.x, point.y);
}
paint.setColor(Color.RED);
paint.setStrokeWidth(4);
canvas.drawPath(path, paint);
}
//迭代绘制集合
private void drawData(Canvas canvas, List data, float fraction) {
if (data.size() == 1) {
drawPoint(canvas, data, Color.BLACK);
destPoints.add(data.get(0));
drawPath(canvas, destPoints);
} else {
drawLine(canvas, data, colors.get(data.size() - 1));
//迭代
List subData = getSubData(data, fraction);
drawData(canvas, subData, fraction);
}
}
private void startAnim() {
ValueAnimator animator = ValueAnimator.ofFloat(0, 100);
animator.setInterpolator(new LinearInterpolator());
animator.setDuration(5000);
animator.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
@Override
public void onAnimationUpdate(ValueAnimator animation) {
fraction = animation.getAnimatedFraction();
invalidate();
}
});
animator.start();
}
//生成随机颜色
private int getRanColor() {
return 0xff000000 | new Random().nextInt(0x00ffffff);
}
//获取子数据源
private List getSubData(List data, float fraction) {
List subData = new ArrayList<>();
for (int i = 0; i < data.size() - 1; i++) {
PointF start = data.get(i);
PointF end = data.get(i + 1);
float x = evaluator.evaluate(fraction, start.x, end.x);
float y = evaluator.evaluate(fraction, start.y, end.y);
subData.add(new PointF(x, y));
}
return subData;
}
}
1.2.生成贝塞尔曲线-De Casteljau算法
package com.che.chechengwang.support.view.bezier;
import android.animation.ValueAnimator;
import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.Path;
import android.graphics.PointF;
import android.util.AttributeSet;
import android.view.View;
import android.view.animation.LinearInterpolator;
import java.util.ArrayList;
import java.util.List;
/**
* 生成贝塞尔曲线-De Casteljau算法
*
* 作者:余天然 on 16/6/14 下午2:10
*/
public class BezierGenerater2 extends View {
private Paint paint;
private int centerX, centerY;
private List points;
private float fraction;
private List destPoints;
public BezierGenerater2(Context context, AttributeSet attrs) {
super(context, attrs);
init();
}
private void init() {
paint = new Paint();
paint.setAntiAlias(true);
paint.setStyle(Paint.Style.STROKE);
}
//初始化数据点和控制点的位置
@Override
protected void onSizeChanged(int w, int h, int oldw, int oldh) {
super.onSizeChanged(w, h, oldw, oldh);
centerX = w / 2;
centerY = h / 2;
points = new ArrayList<>();
points.add(new PointF(centerX - 150, centerY));
points.add(new PointF(centerX - 50, centerY - 300));
points.add(new PointF(centerX + 50, centerY + 300));
points.add(new PointF(centerX + 150, centerY));
destPoints = new ArrayList<>();
destPoints.add(points.get(0));
startAnim();
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
//静态的
drawPoint(canvas, points, Color.BLACK);
drawLine(canvas, points, Color.GRAY);
//动态的
drawPath(canvas, destPoints);
}
// 绘制数据点
private void drawPoint(Canvas canvas, List data, int color) {
paint.setColor(color);
paint.setStrokeWidth(20);
for (int i = 0; i < data.size(); i++) {
PointF pointF = data.get(i);
canvas.drawPoint(pointF.x, pointF.y, paint);
}
}
//绘制基准线
private void drawLine(Canvas canvas, List data, int color) {
paint.setColor(color);
paint.setStrokeWidth(4);
for (int i = 0; i < data.size() - 1; i++) {
PointF start = data.get(i);
PointF end = data.get(i + 1);
canvas.drawLine(start.x, start.y, end.x, end.y, paint);
}
}
//绘制路径
private void drawPath(Canvas canvas, List data) {
Path path = new Path();
PointF start = data.get(0);
path.moveTo(start.x, start.y);
for (int i = 1; i < data.size() - 1; i++) {
PointF point = data.get(i);
path.lineTo(point.x, point.y);
}
paint.setColor(Color.RED);
paint.setStrokeWidth(4);
canvas.drawPath(path, paint);
}
private void startAnim() {
ValueAnimator animator = ValueAnimator.ofFloat(0, 100);
animator.setInterpolator(new LinearInterpolator());
animator.setDuration(5000);
animator.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
@Override
public void onAnimationUpdate(ValueAnimator animation) {
fraction = animation.getAnimatedFraction();
PointF pointF = deCasteljau(fraction, points);
destPoints.add(pointF);
invalidate();
}
});
animator.start();
}
//深复制
private List copyData(List points) {
List data = new ArrayList<>();
for (int i = 0; i < points.size(); i++) {
PointF point = points.get(i);
data.add(new PointF(point.x, point.y));
}
return data;
}
//De Casteljau算法
public PointF deCasteljau(float fraction, List points) {
List data = copyData(points);
final int n = data.size();
for (int i = 1; i <= n; i++) {
for (int j = 0; j < n - i; j++) {
data.get(j).x = (1 - fraction) * data.get(j).x + fraction * data.get(j + 1).x;
data.get(j).y = (1 - fraction) * data.get(j).y + fraction * data.get(j + 1).y;
}
}
return data.get(0);
}
}
1.3.二阶贝塞尔曲线
package com.che.chechengwang.support.view.bezier;
import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.Path;
import android.graphics.PointF;
import android.util.AttributeSet;
import android.view.MotionEvent;
import android.view.View;
/**
* 二阶贝塞尔曲线
*
* 两个数据点和一个控制点
* 公式:B(t) = (1 - t)^2 * P0 + 2t * (1 - t) * P1 + t^2 * P2, t ∈ [0,1]
* 作者:余天然 on 16/6/14 上午10:27
*/
public class Bezier2 extends View {
private Paint paint;
private int centerX, centerY;
private PointF start, end, control;
public Bezier2(Context context, AttributeSet attrs) {
super(context, attrs);
init();
}
private void init() {
paint = new Paint();
paint.setAntiAlias(true);
paint.setStyle(Paint.Style.STROKE);
start = new PointF(0, 0);
end = new PointF(0, 0);
control = new PointF(0, 0);
}
//初始化数据点和控制点的位置
@Override
protected void onSizeChanged(int w, int h, int oldw, int oldh) {
super.onSizeChanged(w, h, oldw, oldh);
centerX = w / 2;
centerY = h / 2;
start.x = centerX - 200;
start.y = centerY;
end.x = centerX + 200;
end.y = centerY;
control.x = centerX;
control.y = centerY - 100;
}
//根据触摸位置更新控制点,并提示重绘
@Override
public boolean onTouchEvent(MotionEvent event) {
control.x = event.getX();
control.y = event.getY();
invalidate();
return true;
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
drawPoint(canvas);
drawGuideLine(canvas);
drawBezierCurve(canvas);
}
// 绘制数据点和控制点
private void drawPoint(Canvas canvas) {
paint.setColor(Color.GRAY);
paint.setStrokeWidth(20);
canvas.drawPoint(start.x, start.y, paint);
canvas.drawPoint(end.x, end.y, paint);
canvas.drawPoint(control.x, control.y, paint);
}
//绘制辅助线
private void drawGuideLine(Canvas canvas) {
paint.setStrokeWidth(4);
canvas.drawLine(start.x, start.y, control.x, control.y, paint);
canvas.drawLine(control.x, control.y, end.x, end.y, paint);
}
//绘制贝塞尔曲线
private void drawBezierCurve(Canvas canvas) {
paint.setColor(Color.RED);
paint.setStrokeWidth(4);
Path path = new Path();
path.moveTo(start.x, start.y);
path.quadTo(control.x, control.y, end.x, end.y);
canvas.drawPath(path, paint);
}
}
1.4.三阶贝塞尔曲线
package com.che.chechengwang.support.view.bezier;
import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.Path;
import android.graphics.PointF;
import android.util.AttributeSet;
import android.view.MotionEvent;
import android.view.View;
import java.util.ArrayList;
import java.util.List;
/**
* 三阶贝塞尔曲线
*
* 2个数据点和2个控制点
* 公式:B(t) = P0 * (1-t)^3 + 3 * P1 * t * (1-t)^2 + 3 * P2 * t^2 * (1-t) + P3 * t^3 代
* 作者:余天然 on 16/6/14 上午10:27
*/
public class Bezier3 extends View {
private Paint paint;
private int centerX, centerY;
private List points;
public Bezier3(Context context, AttributeSet attrs) {
super(context, attrs);
init();
}
private void init() {
paint = new Paint();
paint.setAntiAlias(true);
paint.setStyle(Paint.Style.STROKE);
}
//初始化数据点和控制点的位置
@Override
protected void onSizeChanged(int w, int h, int oldw, int oldh) {
super.onSizeChanged(w, h, oldw, oldh);
centerX = w / 2;
centerY = h / 2;
points = new ArrayList<>();
points.add(new PointF(centerX - 150, centerY));
points.add(new PointF(centerX - 50, centerY - 300));
points.add(new PointF(centerX + 50, centerY + 300));
points.add(new PointF(centerX + 150, centerY));
}
//根据触摸位置更新控制点,并提示重绘
@Override
public boolean onTouchEvent(MotionEvent event) {
PointF control = new PointF(0, 0);
control.x = event.getX();
control.y = event.getY();
double distance1 = getDistance(control, points.get(1));
double distance2 = getDistance(control, points.get(2));
if (distance1 < distance2) {
points.set(1, control);
} else {
points.set(2, control);
}
invalidate();
return true;
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
drawPoint(canvas, points, Color.BLACK);
drawLine(canvas, points, Color.GRAY);
drawBezierCurve(canvas);
}
// 绘制数据点
private void drawPoint(Canvas canvas, List data, int color) {
paint.setColor(color);
paint.setStrokeWidth(20);
for (int i = 0; i < data.size(); i++) {
PointF pointF = data.get(i);
canvas.drawPoint(pointF.x, pointF.y, paint);
}
}
//绘制基准线
private void drawLine(Canvas canvas, List data, int color) {
paint.setColor(color);
paint.setStrokeWidth(4);
for (int i = 0; i < data.size() - 1; i++) {
PointF start = data.get(i);
PointF end = data.get(i + 1);
canvas.drawLine(start.x, start.y, end.x, end.y, paint);
}
}
//绘制贝塞尔曲线
private void drawBezierCurve(Canvas canvas) {
paint.setColor(Color.RED);
paint.setStrokeWidth(4);
Path path = new Path();
path.moveTo(points.get(0).x, points.get(0).y);
path.cubicTo(points.get(1).x, points.get(1).y, points.get(2).x, points.get(2).y, points.get(3).x, points.get(3).y);
canvas.drawPath(path, paint);
}
//获取两点的距离
private double getDistance(PointF start, PointF end) {
return Math.sqrt((end.y - start.y) * (end.y - start.y) + (end.x - start.x) * (end.x - start.x));
}
}
1.5.用贝塞尔曲线拟合圆形
分成四段3阶贝塞尔曲线
每一段拟合90度扇形
计算过程:
也就是:
由公式:B(t) = P0 * (1-t)^3 + 3 * P1 * t * (1-t)^2 + 3 * P2 * t^2 * (1-t) + P3 * t^3
显然,当t=0.5的时候,应该正好在45度的位置上,
于是: sin(pi/4) = 0.125(3x1 - 2) + 0.25(3 - 6x1 ) + 0.5(3x1 )
解出x1=0.55228475

根据对称性,可得y1=x1;
2.自定义视图
贝塞尔曲线就是PS里面的魔棒工具,UI上的很多曲线,其实都是用贝塞尔曲线画的,既然如此,我们只需要知道UI是怎么画的,让她标注好数据点的位置,那我们就可以原样画出UI效果了。
贝塞尔曲线的用处,就是动态绘制平滑曲线!并且可以实时控制曲线状态,并可以通过改变控制点的状态实时让曲线进行平滑的状态变化。
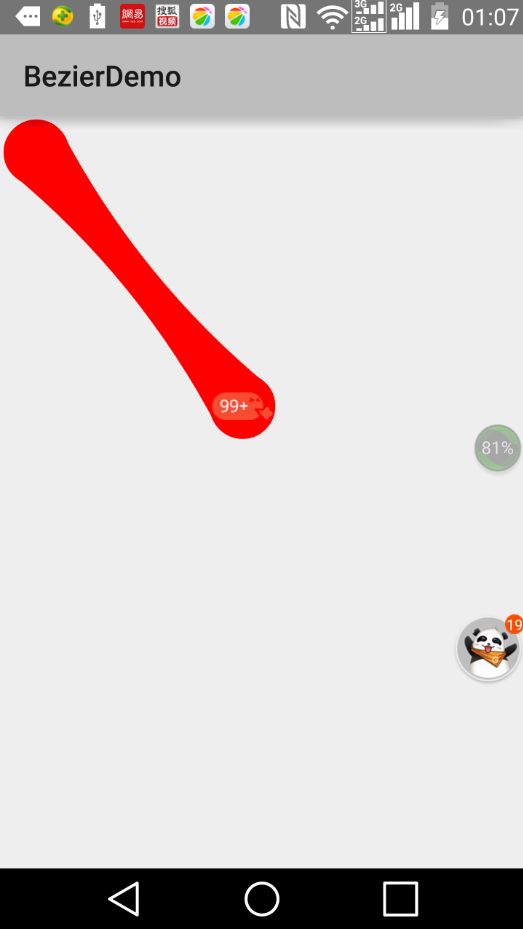
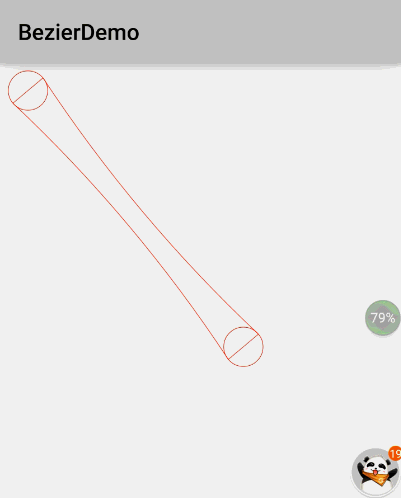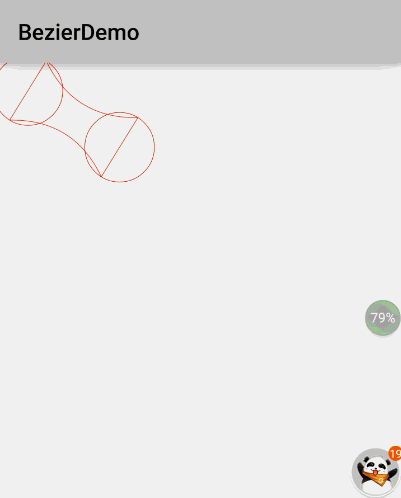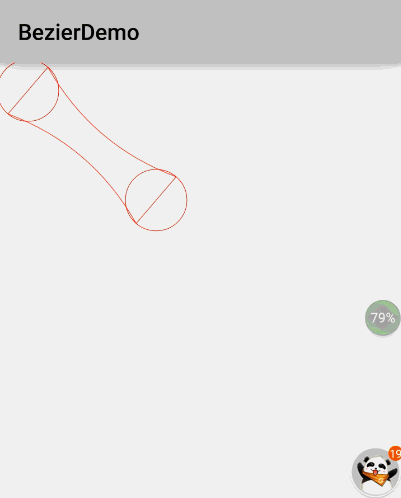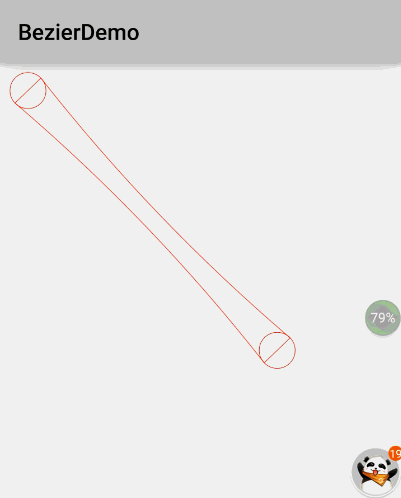
2.1.气泡拖拽效果效果图:
上面的图是盗来的,因为我还不会在手机上录制gif,下面的我的demo的截图:这里:
p1是初始圆的圆心,p2是拖动圆的圆心
X是p1p2线段的中点
AB:与p1p2线段垂直,长度为初始圆的直径
CD:与p1p2线段垂直,长度为拖动圆的直径
绘制流程:
1.绘制p1和p2的圆形
2.根据A,X,D绘制一条2阶贝塞尔曲线
3.根据B,X,C绘制另一条2阶贝塞尔曲线
4.设置path的模式为填充模式
package com.che.chechengwang.support.view.bezier;
import android.animation.FloatEvaluator;
import android.animation.ValueAnimator;
import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.Path;
import android.graphics.PointF;
import android.util.AttributeSet;
import android.view.MotionEvent;
import android.view.View;
import android.view.animation.OvershootInterpolator;
import com.che.chechengwang.support.view.bezier.PointUtil;
/**
* 贝塞尔曲线-气泡拖拽
*
* 二条2阶贝塞尔曲线
* 作者:余天然 on 16/6/14 上午10:27
*/
public class BezierDraggableFlag extends View {
private Paint paint;
private int raduis = 40;//气泡的半径
private double distance;//记录拉动的距离
private double raduisTmp;//临时的半径
private int maxDistance = 800;//拉断的距离
private PointF p1, p2;//圆心
private PointF pA, pB, pC, pD, pX;//控制点
private double distanceBackup;
private PointF p2Backup;
public BezierDraggableFlag(Context context, AttributeSet attrs) {
super(context, attrs);
init();
}
//初始化圆心的位置
private void init() {
paint = new Paint();
paint.setAntiAlias(true);
p1 = new PointF(600, 400);
p2 = new PointF(600, 400);
}
@Override
public boolean onTouchEvent(MotionEvent event) {
switch (event.getAction()) {
case MotionEvent.ACTION_DOWN:
break;
case MotionEvent.ACTION_MOVE:
p2.x = event.getX();
p2.y = event.getY();
distance = PointUtil.getDistance(p1, p2);
invalidate();
break;
case MotionEvent.ACTION_UP:
if (distance < maxDistance) {
p2Backup = new PointF(p2.x, p2.y);
distanceBackup = distance;
startAnim();
}
break;
}
return true;
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
if (distance < maxDistance) {
calculatePoint();
drawBefore(canvas);
} else {
drawAfter(canvas);
}
}
//计算控制点的位置
private void calculatePoint() {
double raduisScale = 1 - distance / maxDistance;
raduisTmp = raduis * raduisScale;
pA = PointUtil.getRotatePoint(p1, p2, raduisTmp, Math.PI / 2);
pB = PointUtil.getRotatePoint(p1, p2, raduisTmp, -Math.PI / 2);
pC = PointUtil.getRotatePoint(p2, p1, raduis, -Math.PI / 2);
pD = PointUtil.getRotatePoint(p2, p1, raduis, Math.PI / 2);
pX = PointUtil.getCenterPoint(p1, p2);
}
//拉断之后的绘制
private void drawAfter(Canvas canvas) {
paint.setColor(Color.RED);
paint.setStyle(Paint.Style.FILL);
paint.setStrokeWidth(4);
canvas.drawCircle(p2.x, p2.y, raduis, paint);
}
//拉断之前的绘制
private void drawBefore(Canvas canvas) {
//端点
// paint.setColor(Color.GRAY);
// paint.setStyle(Paint.Style.STROKE);
// paint.setStrokeWidth(20);
// canvas.drawPoint(p1.x, p1.y, paint);
// canvas.drawPoint(p2.x, p2.y, paint);
// canvas.drawPoint(pX.x, pX.y, paint);
//辅助线
paint.setColor(Color.GRAY);
paint.setStyle(Paint.Style.STROKE);
paint.setStrokeWidth(4);
canvas.drawLine(p1.x, p1.y, p2.x, p2.y, paint);
//文字
// paint.setColor(Color.BLACK);
// paint.setStyle(Paint.Style.FILL);
// paint.setStrokeWidth(2);
// paint.setTextSize(30);
// canvas.drawText("A", pA.x, pA.y, paint);
// canvas.drawText("B", pB.x, pB.y, paint);
// canvas.drawText("C", pC.x, pC.y, paint);
// canvas.drawText("D", pD.x, pD.y, paint);
// canvas.drawText("X", pX.x, pX.y, paint);
// canvas.drawText("p1", p1.x, p1.y, paint);
// canvas.drawText("p2", p2.x, p2.y, paint);
//圆形
paint.setColor(Color.RED);
paint.setStyle(Paint.Style.FILL);
paint.setStrokeWidth(4);
canvas.drawCircle(p1.x, p1.y, (float) raduisTmp, paint);
canvas.drawCircle(p2.x, p2.y, raduis, paint);
//贝塞尔曲线
paint.setColor(Color.RED);
paint.setStyle(Paint.Style.FILL);
paint.setStrokeWidth(4);
Path path = new Path();
path.moveTo(pA.x, pA.y);
path.quadTo(pX.x, pX.y, pD.x, pD.y);
path.lineTo(pC.x, pC.y);
path.quadTo(pX.x, pX.y, pB.x, pB.y);
path.lineTo(pA.x, pA.y);
canvas.drawPath(path, paint);
}
//放开之后,如果没有拉断,就恢复初始状态
private void startAnim() {
final FloatEvaluator evaluator = new FloatEvaluator();
ValueAnimator animator = ValueAnimator.ofFloat(0, 100);
animator.setInterpolator(new OvershootInterpolator());
animator.setDuration(100);
animator.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
@Override
public void onAnimationUpdate(ValueAnimator animation) {
float fraction = animation.getAnimatedFraction();
p2.x = evaluator.evaluate(fraction, p2Backup.x, p1.x);
p2.y = evaluator.evaluate(fraction, p2Backup.y, p1.y);
distance = evaluator.evaluate(fraction, distance, 0);
invalidate();
}
});
animator.start();
}
}
这里用到了一个工具类:
package com.che.chechengwang.support.view.bezier;
import android.graphics.PointF;
/**
* 点计算工具类
*
* 作者:余天然 on 16/6/15 下午2:33
*/
public class PointUtil {
//获取旋转后的点
public static PointF getRotatePoint(PointF p1, PointF p2, double raduis, double radians) {
double oldRadians = getPointDegree(p1, p2);
double newRadians = oldRadians + radians;
float x = (float) (raduis * Math.cos(newRadians));
float y = (float) (raduis * Math.sin(newRadians));
return new PointF(p1.x + x, p1.y + y);
}
//获取中间的点
public static PointF getCenterPoint(PointF p1, PointF p2) {
float x = (p1.x + p2.x) / 2;
float y = (p1.y + p2.y) / 2;
return new PointF(x, y);
}
//获取两点的角度-返回的是弧度制
public static double getPointDegree(PointF p1, PointF p2) {
double scale = (p2.y - p1.y) / (p2.x - p1.x);
return Math.atan(scale);
}
//获取两点的距离
public static double getDistance(PointF start, PointF end) {
return Math.sqrt((end.y - start.y) * (end.y - start.y) + (end.x - start.x) * (end.x - start.x));
}
}
2.2.指示器效果目标效果:
这个以后再来玩,其实有了上面的气泡拖拽效果,实现这个效果很简单的,有兴趣的朋友完全可以根据我上面的效果来实现它。
随便再给大家分享一个学习android自定义View相关知识的好网站:有心课堂-三杆火枪干掉自定义View,传递给你的不仅仅是技术!
菜鸟一枚,水平有限,欢迎大家指出博文中的不足之处,小鱼将不胜感激!@qq:630709658
参考目录:
- 贝塞尔曲线 总结
- BezierDemo源码解析-实现qq消息气泡拖拽消失的效果
- 贝塞尔曲线扫盲
- Path之贝塞尔曲线
- 使用贝塞尔曲线拟合圆
- 基于贝塞尔曲线的Android动画差值器