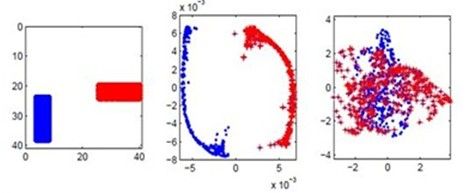
- 在 React 中根据数值动态设置 SVG 线条粗细
啃火龙果的兔子
开发DEMOreact.js前端前端框架
在React中根据数值动态设置SVG线条粗细在React中,你可以根据不同的数值动态设置SVG元素的粗细(stroke-width)。以下是几种实现方式:方法1:直接根据props设置stroke-widthconstDynamicSVG=({thickness})=>();//使用示例//粗线//细线方法2:根据数值范围映射不同粗细constgetStrokeWidth=(value)=>{if
- 东北的冬天黑的真早
张春吉
最近几天白天的时间明显变短了,不到晚上五点钟就要黑天了。实行课后服务以来,我们的下班时间是下午的四点五十,出校门不远就要黑天了,从乡镇会到市里最少要四十分钟的时间,如果堵车可能会一个小时的时间,六点钟到家已经是万家灯火了,小区里的大妈们已经开始了她们的广场舞活动了。下班后到家,十分的疲惫,毕竟上了一天的班,还要开这么久的车,只想在床上躺着。爱人和我一起到家,她负责做饭,半个小时左右后简单的吃点,也
- 读《上下五千年》有感
林子的阅读时光
解放街小学四年级(5)班石谨铭中国五千年历史,是每个炎黄子孙,都非常骄傲的。而中国历史,不仅留下了丰富的文化遗产,还留下了老祖宗的智慧,不仅有《论语》《孟子》《墨子》《春秋》等历史学说。还有《孙子兵法》等著名兵法。《上下五千年》这本书总结了中华民族5000年历史,留下了许许多多的历史人物。中华历史中有明君唐太宗,也有暴君纣王,有可歌可泣的秦始皇,也有卧薪尝胆的越王勾践。当然,那些英雄们有悲壮的荆轲
- 山水之间,择一事终一生
拾光宇宙
艺术源于画家对生活的热爱。在姜子龙老师的世界里,竹便是他全部的生活,三十多年来,与竹为伴,笔墨浸染,直抒写竹人生。他爱竹成痴,敬竹成魔,三十多年如一日,细心观察竹的生长和四季习性,用心感悟竹之精神。这个浮躁时代,坚持是一种稀缺资源。坚持是一件耗费心力的事,是一件从一而终的事,是一件无法回头的事。但只要是自己选择的,再苦再累,坚持往前走,属于你的风景终会出现。胡适说,生命本没有意义,你要能给他什么意
- 题梨花初放
岠山剑客
题梨树初花文/岠山剑客梨花院子外面的小路边,那是哪一年生出一棵树,有认识的路人说梨树,但是得拆,不拆不结果,但是我们谁也不会。四五年的等待,长到拳头粗细,在这个春天到来的时候,绽放几穗翩然的花絮,洁白温润,灵动秀丽,引起我和我的邻居们在花下讨论,关于美丽,关于动人心扉,关于岁月的经历。用手机软件识别,一次,两次,防止不准,三次,四次,每次的结果指向:梨花。总还是感觉和果园里的梨树有点差异,可能,或
- 2022年6月时间开销总结与计划
克克克阿
2022年6月本月的重心就是实习工作,没别的了。下月计划:7月份确定好机票事宜,7月底看看父母和老朋友,再找点课上。睡眠休息:244h2m。日均8.13小时,平均每天再加上午休40分钟左右,大概日剧8.8小时。工作:222h28m。日均工作8.5-9小时左右。吃漱杂事:72h5m。主要是四个周末每天日均6小时左右,工作日一般没算。运动:66h58m。打羽毛球大概20次,付费的大概15次,有一周每天
- Objective-C实现2 个数字之间的算术几何平均值算法(附完整源码)
源代码大师
objective-c算法开发语言
Objective-C实现2个数字之间的算术几何平均值算法算术几何平均值(Arithmetic-GeometricMean,AGM)是一个在数值分析中非常重要的概念,尤其是在计算平方根和其他数学运算时。算术几何平均值是两个正数的算术平均值和几何平均值的迭代过程,直到两个值收敛为止。以下是一个用Objective-C实现的算术几何平均值算法的完整源码:#importdoublearithmeticG
- 能设计算法的,终究是极少数人
奇妙的奇
图片发自App听吴伯凡的《认知方法论》,对“算法”有了全新的认识。世界上最早的程序员比第一台计算机要早一百多年,19世纪初期,法国人雅卡尔,就发明了穿孔纸带控制的纺织机,准确说是纺织提花机,这就是后来计算机用的纸带打孔机的原型,这就是算法。更早,1796年,瑞士人法布尔发明了八音盒。在一个轮子上做一些凸起,随着轮子转动,就能够驱使八音盒奏出制定的乐曲。再早呢?可以往前推演很多。所谓的编制算法,就是
- 员村美食(二)
fun麦兜
梁记猪红汤,在员村菜市场往上走,昌乐园小区入口处。一看菜单就可以看出,价格非常亲民,基本都是10元以下。图一是牛筋丸米粉,四颗牛肉丸,劲道有嚼劲,与潮汕牛肉丸无异。这个份量去到其他地方,至少10以上了。猪红汤也很好吃,4块钱就有一碗了。这家店开在小区内,平常顾客很多,大都是附近居民。图片发自App图片发自App图片发自App图片发自App
- 复盘从一点一滴做起
娟子爱写作
昨天做了第一个比较正式的复盘,按照笔盖导师的话开始了正规复盘。今天落实行动。复盘不是目的,是要理清思路,开始第二天的行动。如果只是写复盘,不去认真地做,只能练练文采而已。改好了形象照片,构思出了创意听里的课程,新梦想写作训练营有四位朋友入群。线下老大哥可能会成为95元第一个付费成员。这些是我不断复盘带来的结果。在泽宇教育里就是要以结果为导向,没有结果,再华丽的词藻都是浪费。
- 如何判断一个男人未来是贫穷,还是富有?从四个方面可以判断
LY遇见小媛
在大众眼中,有一个观念,那就是:作为女人,干得好不如嫁得好。通俗来讲,就是说,在一段婚姻中,女人若是嫁给一个非富即贵的男人,那么,就能实现阶级的跨越。当然,这对女人来说是一件好事。但是,并非每个女人都有这么好的运气。毕竟,优秀的男人都有自己的择偶观,你若不能投其所好,成功的男人于你来说,只能望尘莫及。但是,在现实生活中,很多男人也不是先天富有,而是经过后天努力才能取得成功。这就是我们常说的“大器晚
- 2020-07-04【金钱在哪里?】课后三问
陈二利
你所未知的领悟~一,我学到了什么?钱在哪里?①,钱在问题里。②,钱在思想里。③,钱在消费里。④,钱在对手里。每天要完成四件事!每天去帮助五个人!要成为一个高价咨询师。。。当你越垂直,越细分的时候,你的对手都在为你引流。。。。能解决别人问题的人,此生就会变得越来越富!【双益思维】~左手公益,右手受益。左手足够多,右手才有挑的余地。。二,我的灵感是什么?叮咚!我的灵感是~先要有思想,然后有行动。再者就
- 穿越战争故事《2029,世界公敌》第十七章 秘鲁的毒枭(四)
续事创意写作工作室
【目录】穿越战争故事《2029,世界公敌》空中星光灿烂,山下万家灯火。吃过晚饭,李昇约着肯普一同向健身房走去,这是梅尔森为自己设置健身房,也刚好方便了李昇他们训练。肯普系好鞋带,看了看自己的运动鞋。“他们这鞋还挺合脚。”李昇也穿好了衣服:“走吧。”走出换衣间,偌大的健身房里空无一人,两人走向跑步机热身。“总部联系上了吗?”“没有,但有些发现。”“据我分析咱们的手环皮下植入的应该是一个GPS的信号发
- 飞算JavaAI:Java开发者的智能革命,从代码生成到架构重塑
目录一、Java开发困局:效率与质量的双重挑战二、技术架构解析:三层智能引擎驱动开发革命1.智能语义理解层2.代码智能生成层3.运行时智能优化层三、核心功能矩阵:从需求到部署的全流程覆盖1.智能需求分析2.自动化软件设计3.工程化代码输出4.智能重构引擎四、实战场景解析:从初创项目到老系统改造场景1:初创项目快速验证场景2:老系统迭代升级场景3:高并发系统优化五、开发者价值重构:从代码工人到系统设
- 飞算 JavaAI 深度体验:开启 Java 开发智能化新纪元
♡喜欢做梦
飞算JavaAI炫技赛Java开发
个人主页:♡喜欢做梦欢迎点赞➕关注❤️收藏评论目录一、引言二、飞算JavaAI初印象与功能概览(一)初识(二)核心功能模块概览三、智能代码生成功能深度体验(一)基础场景测试(二)复杂业务逻辑场景(三)代码生成功能总结四、代码优化建议功能测评(一)测试用例准备(二)优化建议(三)进一步复杂代码测试(四)代码优化功能总结五、故障诊断与修复功能实践(一)模拟常见Java故障场景一、引言在当今软件开发领域
- 十大经典排序算法——冒泡排序
—————————————————
算法排序排序算法算法
冒泡排序(BubbleSort)是一种简单的排序算法,它通过重复地遍历待排序的列表,比较相邻的元素并交换它们的位置来实现排序。该算法的名称来源于较小的元素会像"气泡"一样逐渐"浮"到列表的顶端。一、算法步骤比较相邻元素:从列表的第一个元素开始,比较相邻的两个元素。交换位置:如果前一个元素比后一个元素大,则交换它们的位置。重复遍历:对列表中的每一对相邻元素重复上述步骤,直到列表的末尾。这样,最大的元
- LLM - 通过案例轻松理解MCP、Tool Calling、Agent
小小工匠
【LLM大模型】MCPFunctionCallAgentToolCalling
文章目录一、MCP是什么?二、MCP解决了哪些痛点?三、什么是ToolCalling?四、对比案例一:ToolCallingvsMCP五、对比案例二:AgentvsAgent+MCP六:使用场景理解Agent→ToolCalling→MCP场景一:智能助手帮你整理工作安排(重构版)Agent的理解与规划ToolCalling的执行流程MCP的幕后支撑场景二:智能电商客服处理订单异常Agent的理解
- 忍痛割爱
六月荷清香
图片发自App我的胸口痛的老毛病伴随我有十几年了。每次受了寒就会发作,每次发作来势汹汹,连准备都没有,我会胸闷得透不过气来,痛得额头上冷汗直冒,而四肢则冰凉。紧接着这种闷痛直达后背部,又胀又痛,让人极不舒服。每次病发作了,我都会冒出一个念头,这么难受,还不如让我去死。如果我家男人在家,他会快速地拿家里早就准备好的艾叶,倒上一盆热气腾腾的开水泡上,丢上一勺盐,然后撩起我的衣服,露出后背,用泡得滚烫的
- 第7章- 迈向新的旅程(1/2)
黑羽雪桐
数千名士兵甚至是紫辉境的布德都被这一招瞬间冻结住,紧接着紫黑色的火焰将他们燃烧殆尽,连一丝灰尘都没剩下。眨眼间,四周变得空荡荡的,要不是苍月亲眼所见,她真的难以相信刚才那几千号人就这么被炎兰给干掉了。似乎魔力透支的炎兰瞬间单膝跪在地上,依靠地上竖起的剑勉强没有倒下去。“炎兰,你没事吧!”苍月扶起炎兰关心的问道。“啊,没什么大事,只是魔力好像耗尽了,刚才那一下要是没给玛多姆致命一击的话,待会想要打败
- VUE解决Error: error:0308010C:digital envelope routines::unsupported的四种解决方案
问题描述:报错:Error:error:0308010C:digitalenveloperoutines::unsupported报错原因:主要是因为nodeJsV17版本发布了OpenSSL3.0对算法和秘钥大小增加了更为严格的限制,nodeJsv17之前版本没影响,但V17和之后版本会出现这个错误。我的node版本是v18+报错详细信息:rror:error:0308010C:digitale
- 天文图像处理:星系分类与天体定位
xcLeigh
计算机视觉CV图像处理分类人工智能AI计算机视觉
天文图像处理:星系分类与天体定位一、前言二、天文图像处理基础2.1天文图像的获取2.2天文图像的格式2.3天文图像处理的基本流程三、天文图像预处理3.1去噪处理3.2平场校正3.3偏置校正四、星系分类4.1星系的分类体系4.2基于特征提取的星系分类方法4.3基于深度学习的星系分类方法五、天体定位5.1天体坐标系统5.2基于星图匹配的天体定位方法5.3基于深度学习的天体定位方法六、总结与展望致读者一
- 2019.10.13
蚂蚁_caec
日精进打卡第203天姓名:李敏499期学员努力一组公司:上海缘缀包装材料有限公司【知~学习】《六项精进》1遍,共201遍;《大学》1遍,共201遍未背诵企业使命、愿景、价值观【经典名句分享】付出不亚于任何人的努力一、修身:练字调理身体纠正驼背垃圾分类反省养生二、齐家:与妈妈打电话与骆驼互道早安晚安与骆驼一起做饭三、建功:关注备案信息转发公众号文章关注公司活动沟通奖励票事宜四、【积善】:发愿从201
- JAVA并发编程(四)-park-unpark
imperfectsam
java开发语言
文章目录一、简介二、编写代码三、park和unpark原理一、简介 在Java中,park和unpark是java.util.concurrent.locks包中的LockSupport类提供的两个静态方法,用于线程的阻塞和解除阻塞。1、park方法用于阻塞当前线程,使其进入等待状态。 当一个线程调用park方法时,它会被阻塞,直到发生以下几种情况之一: -另一个线程调用了相应线程的unpa
- AI 人工智能与 Copilot 的融合发展策略
AI天才研究院
AI人工智能与大数据人工智能copilotai
AI人工智能与Copilot的融合发展策略关键词:人工智能、Copilot、代码生成、人机协作、机器学习、自然语言处理、软件开发摘要:本文探讨了人工智能与Copilot技术的融合发展策略。我们将从技术原理、实现方法、应用场景等多个维度深入分析,提出一套完整的融合框架和发展路径。文章首先介绍背景和核心概念,然后详细讲解关键技术,包括自然语言处理、代码生成算法等,接着通过实际案例展示应用效果,最后讨论
- AI 人工智能与 Copilot 碰撞出的火花
AI天才研究院
AI大模型企业级应用开发实战人工智能copilotai
AI人工智能与Copilot碰撞出的火花关键词:AI人工智能、Copilot、代码辅助、智能编程、人机协作、软件开发、技术创新摘要:本文深入探讨了AI人工智能与Copilot碰撞所产生的一系列效应。首先介绍了相关背景,包括目的、预期读者、文档结构和术语表。接着阐述了核心概念与联系,展示了其原理和架构的示意图及流程图。详细讲解了核心算法原理和具体操作步骤,并通过Python代码进行说明。同时给出了数
- 多租户SaaS系统中设计安全便捷的跨租户流程共享
Alex艾力的IT数字空间
安全功能测试架构中间件微服务网络安全代码规范
四维协同架构,结合动态授权、加密传输、行为审计和智能策略一、权限控制体系1.动态权限模型2.授权策略实现RBAC+ABAC混合模型在流程表增加shared_tenants字段存储授权信息,结合属性动态校验:CREATETABLEworkflow_process(process_idVARCHAR(36)PRIMARYKEY,tenant_idVARCHAR(36)NOTNULL,shared_te
- 硬件预取的几个问题 1
1.硬件预取的定义和目标是什么?答案:硬件预取是CPU在程序执行前自动预测并加载可能使用的数据到缓存中的技术,目标是减少缓存未命中带来的延迟,提升指令吞吐量。2.硬件预取与软件预取的核心区别?答案:硬件预取由CPU内部逻辑自动触发,透明且通用;软件预取需程序员显式插入指令(如prefetch),可针对特定场景优化,但依赖代码适配。3.预取算法的主要分类?答案:分为规则驱动型(如顺序、步长预取)和机
- Zuul的用法——限流
HmilyMing
因为所有的对外提供的接口都是要经过Zuul的转发,所以在这里的Pre过滤器里面做限流是最好的。常用的限流算法有1.计数器法,可以看做是低精度的滑动窗口算法2.滑动窗口,需要更多的存储空间3.漏桶算法,4.令牌桶算法,运行流量在一定程度上的突发,实践简单,对用户更友好,采用得更多。我这里采用的就是令牌桶算法,其原理如下令牌桶算法guava里面有令牌桶算法的实现在浏览器多刷几次就会被限流给禁止访问了代
- 如何从热恋走向婚姻结婚,并一直幸福?
有才有闲
↑推荐阅读↑如何在荷尔蒙降低后还能保持甜蜜?爱情中的甜言蜜语和承诺,能不能在婚姻中兑现和延续,取决于双方会不会经营婚姻。只要会经营,还有可能超额完成任务。当然,还有个前提是双方都愿意并且会经营婚姻。(提示:婚姻经营是一门需要学习的学问)这里需要提到在一段关系中我们常说的四个时期:相爱期:大家用尽各种方法得到对方。热恋期:荷尔蒙爆发,粘在一起,什么都没法分开,越反对反而粘的越紧。磨合期:大多数人进入
- C 语言字符大小写互转:tolower / toupper 详解与实战
BabyZZの秘密日记
C语言c语言开发语言
个人主页:BabyZZの秘密日记收入专栏:C语言文章目入一、函数原型二、实现原理(glibc2.39源码节选)三、常见陷阱与最佳实践四、完整示例:大小写不敏感查找子串五、性能扩展:批量转换的SIMD思路六、小结在文本处理、协议解析、命令行解析等场景中,“大小写不敏感”是十分常见的需求。C标准库提供了两个最常用的工具函数:inttolower(intc);——大写→小写inttoupper(intc
- java数字签名三种方式
知了ing
javajdk
以下3钟数字签名都是基于jdk7的
1,RSA
String password="test";
// 1.初始化密钥
KeyPairGenerator keyPairGenerator = KeyPairGenerator.getInstance("RSA");
keyPairGenerator.initialize(51
- Hibernate学习笔记
caoyong
Hibernate
1>、Hibernate是数据访问层框架,是一个ORM(Object Relation Mapping)框架,作者为:Gavin King
2>、搭建Hibernate的开发环境
a>、添加jar包:
aa>、hibernatte开发包中/lib/required/所
- 设计模式之装饰器模式Decorator(结构型)
漂泊一剑客
Decorator
1. 概述
若你从事过面向对象开发,实现给一个类或对象增加行为,使用继承机制,这是所有面向对象语言的一个基本特性。如果已经存在的一个类缺少某些方法,或者须要给方法添加更多的功能(魅力),你也许会仅仅继承这个类来产生一个新类—这建立在额外的代码上。
- 读取磁盘文件txt,并输入String
一炮送你回车库
String
public static void main(String[] args) throws IOException {
String fileContent = readFileContent("d:/aaa.txt");
System.out.println(fileContent);
- js三级联动下拉框
3213213333332132
三级联动
//三级联动
省/直辖市<select id="province"></select>
市/省直辖<select id="city"></select>
县/区 <select id="area"></select>
- erlang之parse_transform编译选项的应用
616050468
parse_transform游戏服务器属性同步abstract_code
最近使用erlang重构了游戏服务器的所有代码,之前看过C++/lua写的服务器引擎代码,引擎实现了玩家属性自动同步给前端和增量更新玩家数据到数据库的功能,这也是现在很多游戏服务器的优化方向,在引擎层面去解决数据同步和数据持久化,数据发生变化了业务层不需要关心怎么去同步给前端。由于游戏过程中玩家每个业务中玩家数据更改的量其实是很少
- JAVA JSON的解析
darkranger
java
// {
// “Total”:“条数”,
// Code: 1,
//
// “PaymentItems”:[
// {
// “PaymentItemID”:”支款单ID”,
// “PaymentCode”:”支款单编号”,
// “PaymentTime”:”支款日期”,
// ”ContractNo”:”合同号”,
//
- POJ-1273-Drainage Ditches
aijuans
ACM_POJ
POJ-1273-Drainage Ditches
http://poj.org/problem?id=1273
基本的最大流,按LRJ的白书写的
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
#define INF 0x7fffffff
int ma
- 工作流Activiti5表的命名及含义
atongyeye
工作流Activiti
activiti5 - http://activiti.org/designer/update在线插件安装
activiti5一共23张表
Activiti的表都以ACT_开头。 第二部分是表示表的用途的两个字母标识。 用途也和服务的API对应。
ACT_RE_*: 'RE'表示repository。 这个前缀的表包含了流程定义和流程静态资源 (图片,规则,等等)。
A
- android的广播机制和广播的简单使用
百合不是茶
android广播机制广播的注册
Android广播机制简介 在Android中,有一些操作完成以后,会发送广播,比如说发出一条短信,或打出一个电话,如果某个程序接收了这个广播,就会做相应的处理。这个广播跟我们传统意义中的电台广播有些相似之处。之所以叫做广播,就是因为它只负责“说”而不管你“听不听”,也就是不管你接收方如何处理。另外,广播可以被不只一个应用程序所接收,当然也可能不被任何应
- Spring事务传播行为详解
bijian1013
javaspring事务传播行为
在service类前加上@Transactional,声明这个service所有方法需要事务管理。每一个业务方法开始时都会打开一个事务。
Spring默认情况下会对运行期例外(RunTimeException)进行事务回滚。这
- eidtplus operate
征客丶
eidtplus
开启列模式: Alt+C 鼠标选择 OR Alt+鼠标左键拖动
列模式替换或复制内容(多行):
右键-->格式-->填充所选内容-->选择相应操作
OR
Ctrl+Shift+V(复制多行数据,必须行数一致)
-------------------------------------------------------
- 【Kafka一】Kafka入门
bit1129
kafka
这篇文章来自Spark集成Kafka(http://bit1129.iteye.com/blog/2174765),这里把它单独取出来,作为Kafka的入门吧
下载Kafka
http://mirror.bit.edu.cn/apache/kafka/0.8.1.1/kafka_2.10-0.8.1.1.tgz
2.10表示Scala的版本,而0.8.1.1表示Kafka
- Spring 事务实现机制
BlueSkator
spring代理事务
Spring是以代理的方式实现对事务的管理。我们在Action中所使用的Service对象,其实是代理对象的实例,并不是我们所写的Service对象实例。既然是两个不同的对象,那为什么我们在Action中可以象使用Service对象一样的使用代理对象呢?为了说明问题,假设有个Service类叫AService,它的Spring事务代理类为AProxyService,AService实现了一个接口
- bootstrap源码学习与示例:bootstrap-dropdown(转帖)
BreakingBad
bootstrapdropdown
bootstrap-dropdown组件是个烂东西,我读后的整体感觉。
一个下拉开菜单的设计:
<ul class="nav pull-right">
<li id="fat-menu" class="dropdown">
- 读《研磨设计模式》-代码笔记-中介者模式-Mediator
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
/*
* 中介者模式(Mediator):用一个中介对象来封装一系列的对象交互。
* 中介者使各对象不需要显式地相互引用,从而使其耦合松散,而且可以独立地改变它们之间的交互。
*
* 在我看来,Mediator模式是把多个对象(
- 常用代码记录
chenjunt3
UIExcelJ#
1、单据设置某行或某字段不能修改
//i是行号,"cash"是字段名称
getBillCardPanelWrapper().getBillCardPanel().getBillModel().setCellEditable(i, "cash", false);
//取得单据表体所有项用以上语句做循环就能设置整行了
getBillC
- 搜索引擎与工作流引擎
comsci
算法工作搜索引擎网络应用
最近在公司做和搜索有关的工作,(只是简单的应用开源工具集成到自己的产品中)工作流系统的进一步设计暂时放在一边了,偶然看到谷歌的研究员吴军写的数学之美系列中的搜索引擎与图论这篇文章中的介绍,我发现这样一个关系(仅仅是猜想)
-----搜索引擎和流程引擎的基础--都是图论,至少像在我在JWFD中引擎算法中用到的是自定义的广度优先
- oracle Health Monitor
daizj
oracleHealth Monitor
About Health Monitor
Beginning with Release 11g, Oracle Database includes a framework called Health Monitor for running diagnostic checks on the database.
About Health Monitor Checks
Health M
- JSON字符串转换为对象
dieslrae
javajson
作为前言,首先是要吐槽一下公司的脑残编译部署方式,web和core分开部署本来没什么问题,但是这丫居然不把json的包作为基础包而作为web的包,导致了core端不能使用,而且我们的core是可以当web来用的(不要在意这些细节),所以在core中处理json串就是个问题.没办法,跟编译那帮人也扯不清楚,只有自己写json的解析了.
- C语言学习八结构体,综合应用,学生管理系统
dcj3sjt126com
C语言
实现功能的代码:
# include <stdio.h>
# include <malloc.h>
struct Student
{
int age;
float score;
char name[100];
};
int main(void)
{
int len;
struct Student * pArr;
int i,
- vagrant学习笔记
dcj3sjt126com
vagrant
想了解多主机是如何定义和使用的, 所以又学习了一遍vagrant
1. vagrant virtualbox 下载安装
https://www.vagrantup.com/downloads.html
https://www.virtualbox.org/wiki/Downloads
查看安装在命令行输入vagrant
2.
- 14.性能优化-优化-软件配置优化
frank1234
软件配置性能优化
1.Tomcat线程池
修改tomcat的server.xml文件:
<Connector port="8080" protocol="HTTP/1.1" connectionTimeout="20000" redirectPort="8443" maxThreads="1200" m
- 一个不错的shell 脚本教程 入门级
HarborChung
linuxshell
一个不错的shell 脚本教程 入门级
建立一个脚本 Linux中有好多中不同的shell,但是通常我们使用bash (bourne again shell) 进行shell编程,因为bash是免费的并且很容易使用。所以在本文中笔者所提供的脚本都是使用bash(但是在大多数情况下,这些脚本同样可以在 bash的大姐,bourne shell中运行)。 如同其他语言一样
- Spring4新特性——核心容器的其他改进
jinnianshilongnian
spring动态代理spring4依赖注入
Spring4新特性——泛型限定式依赖注入
Spring4新特性——核心容器的其他改进
Spring4新特性——Web开发的增强
Spring4新特性——集成Bean Validation 1.1(JSR-349)到SpringMVC
Spring4新特性——Groovy Bean定义DSL
Spring4新特性——更好的Java泛型操作API
Spring4新
- Linux设置tomcat开机启动
liuxingguome
tomcatlinux开机自启动
执行命令sudo gedit /etc/init.d/tomcat6
然后把以下英文部分复制过去。(注意第一句#!/bin/sh如果不写,就不是一个shell文件。然后将对应的jdk和tomcat换成你自己的目录就行了。
#!/bin/bash
#
# /etc/rc.d/init.d/tomcat
# init script for tomcat precesses
- 第13章 Ajax进阶(下)
onestopweb
Ajax
index.html
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/
- Troubleshooting Crystal Reports off BW
blueoxygen
BO
http://wiki.sdn.sap.com/wiki/display/BOBJ/Troubleshooting+Crystal+Reports+off+BW#TroubleshootingCrystalReportsoffBW-TracingBOE
Quite useful, especially this part:
SAP BW connectivity
For t
- Java开发熟手该当心的11个错误
tomcat_oracle
javajvm多线程单元测试
#1、不在属性文件或XML文件中外化配置属性。比如,没有把批处理使用的线程数设置成可在属性文件中配置。你的批处理程序无论在DEV环境中,还是UAT(用户验收
测试)环境中,都可以顺畅无阻地运行,但是一旦部署在PROD 上,把它作为多线程程序处理更大的数据集时,就会抛出IOException,原因可能是JDBC驱动版本不同,也可能是#2中讨论的问题。如果线程数目 可以在属性文件中配置,那么使它成为
- 正则表达式大全
yang852220741
html编程正则表达式
今天向大家分享正则表达式大全,它可以大提高你的工作效率
正则表达式也可以被当作是一门语言,当你学习一门新的编程语言的时候,他们是一个小的子语言。初看时觉得它没有任何的意义,但是很多时候,你不得不阅读一些教程,或文章来理解这些简单的描述模式。
一、校验数字的表达式
数字:^[0-9]*$
n位的数字:^\d{n}$
至少n位的数字:^\d{n,}$
m-n位的数字:^\d{m,n}$