Java循环队列原理与用法详解

本文实例讲述了Java循环队列原理与用法。分享给大家供大家参考，具体如下：

在正式进行循环队列学习之前，我们先来看看在顺序队列中删除队首元素出现的问题

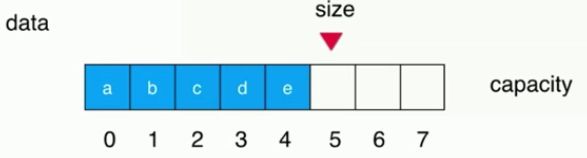
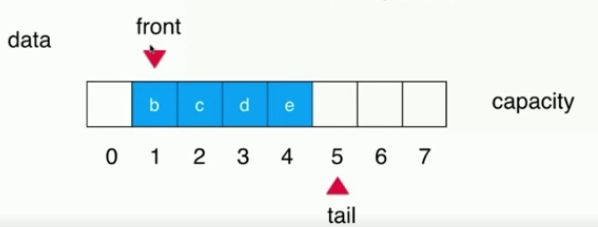
（1）设一个容量为capacity=8，size=5(a,b,c,d,e)的数组，左侧为队首、右侧为队尾。

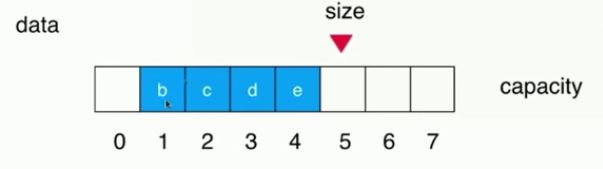
（2）出队一个元素后，需整体往前移动一位

#出队

  

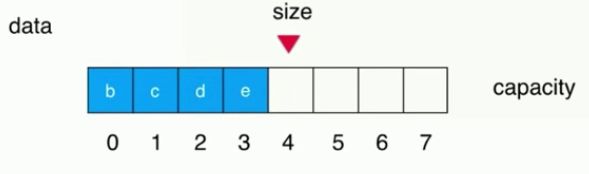
#2整体前移一位

关于该种操作方式我们很容易得出时间复杂度为O(n)。

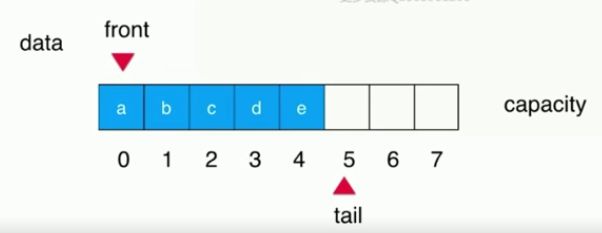
这时我们就想可不可以在出队元素后，整体元素不往前移，而是在数组中记下队首front是谁，同时队尾tail指向在下一次元素入队时的位置，这样当再有出队时只需要维护一下front的指向即可，而不需移动元素。就这样我们就有了循环队列的情况。

2.循环队列原理

(1)初始，数组整体为空时，队首front、队尾tail指向同一个位置（数组索引为0的地方）也即front==tail 时队列为空

 

(2)当往数组中添加元素后，

(3)出队一个元素，front指向新的位置

(4)入队元素，tail叠加

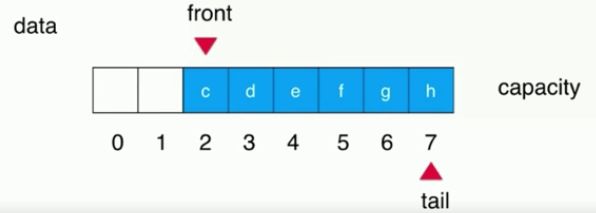
(5)当tail不能再增加时，数组前面还有空余，此时循环队列就该出场了。

 

此时数组应该变为这样：

 在往数组中添加一个元素：

这样数组就已经满了（tail+1==front 队列满），开始出发扩容操作。【capacity中，浪费一个空间】。

为了tail能返回到数组的前面位置，将队列满的表达式变为 【（tail+1）%c==front】这样数组就可以循环移动了。

3.循环队列代码实现

新建一个类LoopQueue并实现接口Queue。

#1：接口Queue代码如下：

package Queue;

public interface Queue {
  //获取队列中元素个数
  int getSize();

  //队列中元素是否为空
  boolean isEmpty();

  //入队列
  void enqueue(E e);

  //出队列
  E dequeue();

  //获取队首元素
  E getFront();
}

#2：LoopQueue相关代码：

package Queue;

//循环队列
public class LoopQueue implements Queue {
  private E[] data;
  private int front, tail;
  private int size;//队列中元素个数

  //构造函数，传入队列的容量capacity构造函数
  public LoopQueue(int capacity) {
    data = (E[]) new Object[capacity + 1];//浪费与一个空间
    front = 0;
    tail = 0;
    size = 0;
  }

  //无参构造函数，默认队列的容量capacity=10
  public LoopQueue() {
    this(10);
  }

  //真正容量
  public int getCapacity() {
    return data.length - 1;
  }

  //队列是否为空
  @Override
  public boolean isEmpty() {
    return front == tail;
  }

  //队列中元素个数
  @Override
  public int getSize() {
    return size;
  }

  //入队列操作
  @Override
  public void enqueue(E e) {
    if ((tail + 1) % data.length == front) {//队列已满，需要扩容
      resize(getCapacity() * 2);
    }
    data[tail] = e;
    tail = (tail + 1) % data.length;
    size++;
  }

  //出队操作

  @Override
  public E dequeue() {
    if (isEmpty()) {
      throw new IllegalArgumentException("队列为空");
    }

    E ret = data[front];
    data[front] = null;//手动释放
    front = (front + 1) % data.length;
    size--;
    if (size == getCapacity() / 4 && getCapacity() / 2 != 0) {
      resize(getCapacity() / 2);
    }
    return ret;
  }

  //获取队首元素
  @Override
  public E getFront() {
    if (isEmpty()) {
      throw new IllegalArgumentException("队列为空");
    }
    return data[front];
  }

  //改变容量
  private void resize(int newCapacity) {
    E[] newData = (E[]) new Object[newCapacity + 1];
    for (int i = 0; i < size; i++) {
      newData[i] = data[(front + i) % data.length];//循环数组防止越界
    }
    data = newData;
    front = 0;
    tail = size;
  }


  @Override
  public String toString() {
    StringBuilder res = new StringBuilder();
    res.append(String.format("Queue:size=%d, capacity=%d\n", size, getCapacity()));
    res.append("front [");
    for (int i = front; i != tail; i = (i + 1) % data.length) {
      res.append(data[i]);
      if ((i + 1) % data.length != tail) {
        res.append(",");
      }
    }
    res.append("] tail");
    return res.toString();
  }



}

在关于LoopQueue类中需要注意的：

（1）第11行中的+1是capacity需要浪费一个空间，故在实例化是多加1

 data = (E[]) new Object[capacity + 1];//浪费与一个空间

（2）地24行真正的容量是data.length-1，这是由于有一个空间是浪费的。

data.length - 1;

（3）关于入队中第46行tail值的说明

为了保证入队是循环操作，tail值的变化规律为

 tail = (tail + 1) % data.length;

（4）关于82行的数据迁移操作，取余操作是为了防止循环数组时越界。

  newData[i] = data[(front + i) % data.length];//循环数组防止越界

#3直接在LoopQueue中添加一个main函数进行测试，相关代码如下：

  //测试用例
  public static void main(String[] args) {
    LoopQueue queue = new LoopQueue();
    for (int i = 0; i < 10; i++) {
      queue.enqueue(i);
      System.out.println(queue);

      if(i%3==2){//每添加3个元素出队列一个
        queue.dequeue();
        System.out.println(queue);
      }

    }

  }

结果为：

 

4.循环队列时间复杂度

到此我们就实现了一个循环队列操作，解决了在顺序队列中出队时的时间复杂度为O(n)的情况，在循环队列中出队的时间复杂度为O(1)。

源码地址 https://github.com/FelixBin/dataStructure/blob/master/src/Queue/LoopQueue.java

更多关于java算法相关内容感兴趣的读者可查看本站专题：《Java数据结构与算法教程》、《Java操作DOM节点技巧总结》、《Java文件与目录操作技巧汇总》和《Java缓存操作技巧汇总》

希望本文所述对大家java程序设计有所帮助。