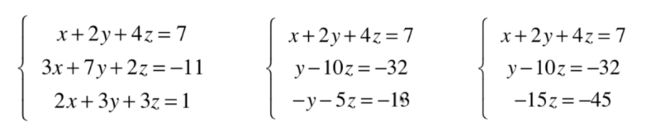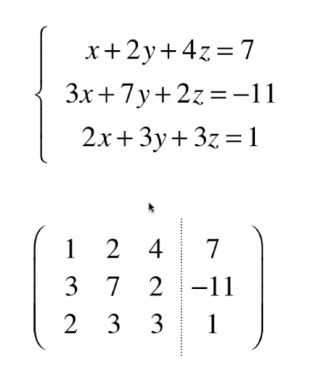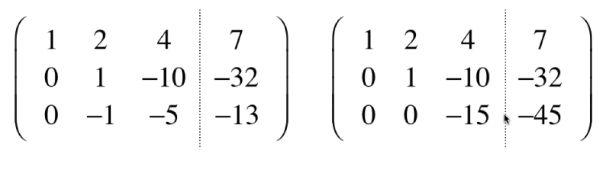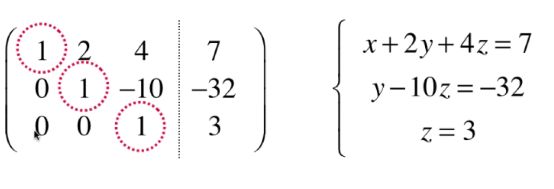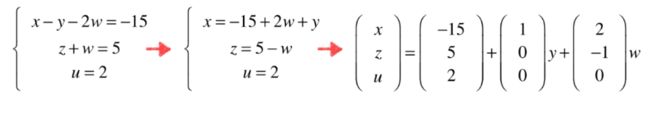线性系统，就是一组线性方程组。所谓线性方程组也就是只允许有X的一次方。
如下图
image.png
那么如何解线性方程组呢？
消元。
image.png
操作分为，一个方程的左右两边同时乘以一个常数，或者一个方程加减另一个方程。
还可以交换2个方程的位置
用矩阵的方式表达这样一个线性系统。
image.png
3行代表3个方程
3列（不算最后一列）代表有3个未知数
算上最后一列的矩阵叫增广矩阵。
image.png
image.png
image.png
-
把方程组写成增广矩阵。
image.png -
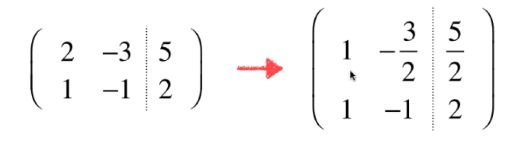
把主对角线的位置依次化为1.
image.png
image.png
3.如果主元的位置为0，我们需要做交换的操作。
image.png
image.png
下面我们该如何让上面的Y和X 都能很直观的看到呢？
我们还是用矩阵的基本操作。
自底向上，用高斯消元。
image.png
image.png
线性系统高斯消元实现：
from .Matrix import Matrix
from .Vector import Vector
class LinearSystem:
def __init__(self, A, b):
assert A.row_num() == len(b)
self._m = A.row_num()
self._n = A.col_num()
assert self._m == self._n
self.Ab = [Vector(A.row_vector(i).underlying_list() + [b[i]])
for i in range(self._m)]
def _max_row(self, index, n):
best, ret = self.Ab[index][index], index
for i in range(index + 1, n):
if self.Ab[i][index] > best:
best, ret = self.Ab[i][index], i
return ret
def _forward(self):
n = self._m
for i in range(n):
#Ab[i][i] 为主元
max_row = self._max_row(i,n)
self.Ab[i], self.Ab[max_row] = self.Ab[max_row], self.Ab[i]
self.Ab[i] = self.Ab[i] / self.Ab[i][i]
for j in range(i + 1, n):
self.Ab[j] = self.Ab[j] - self.Ab[j][i] * self.Ab[i]
def _backward(self):
n = self._m
for i in range(n - 1, - 1, -1):
for j in range(i - 1, -1, -1):
self.Ab[j] = self.Ab[j] - self.Ab[j][i] * self.Ab[i]
def gauss_jordan_elimination(self):
self._forward()
self._backward()
def fancy_print(self):
for i in range(self._m):
print(" ".join(str(self.Ab[i][j]) for j in range(self._n)), end=" ")
print("|", self.Ab[i][-1])
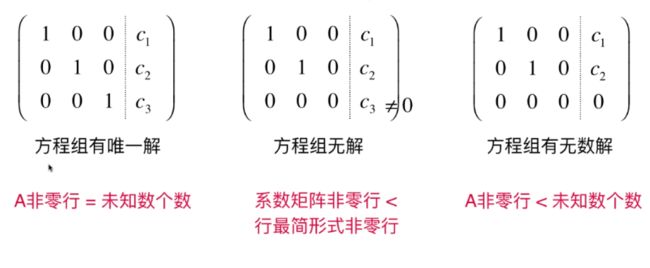
无解
image.png
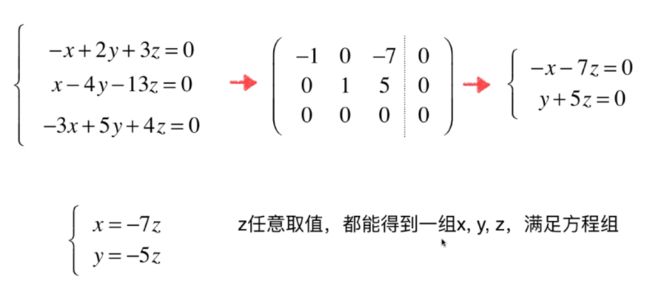
无数个解
image.png
image.png
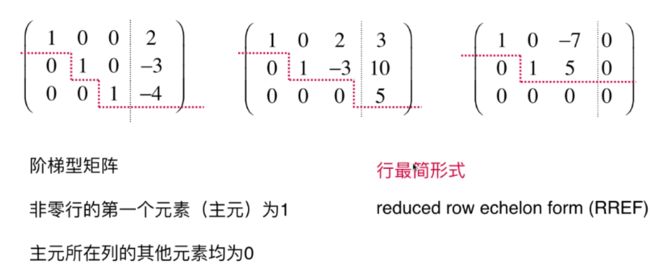
行最简形式
image.png
image.png
方程组解的结构
image.png
image.png
更一般的线性系统求解
image.png
image.png
实现更一般的线性系统
class LinearSystem:
def __init__(self, A, b):
assert A.row_num() == len(b)
self._m = A.row_num()
self._n = A.col_num()
self.Ab = [Vector(A.row_vector(i).underlying_list() + [b[i]])
for i in range(self._m)]
self.pivots = []
def _max_row(self, index_i, index_j, n):
best, ret = self.Ab[index_i][index_j], index_i
for i in range(index_i + 1, n):
if self.Ab[i][index_j] > best:
best, ret = self.Ab[i][index_j], i
return ret
def _forward(self):
i, k = 0, 0
while i < self._m and k < self._n:
#Ab[i][k] 是否可以是主元
max_row = self._max_row(i,k,self._m)
self.Ab[i], self.Ab[max_row] = self.Ab[max_row], self.Ab[i]
if is_zero(self.Ab[i][k]):
k += 1
else:
self.Ab[i] = self.Ab[i] / self.Ab[i][k]
for j in range(i + 1, self._m):
self.Ab[j] = self.Ab[j] - self.Ab[j][k] * self.Ab[i]
self.pivots.append(k)
i += 1
def _backward(self):
n = len(self.pivots)
for i in range(n - 1, - 1, -1):
k = self.pivots[i]
for j in range(i - 1, -1, -1):
self.Ab[j] = self.Ab[j] - self.Ab[j][k] * self.Ab[i]
def gauss_jordan_elimination(self):
self._forward()
self._backward()
for i in range(len(self.pivots), self._m):
if not is_zero(self.Ab[i][-1]):
return False
return True
def fancy_print(self):
for i in range(self._m):
print(" ".join(str(self.Ab[i][j]) for j in range(self._n)), end=" ")
print("|", self.Ab[i][-1])
测试
from playLA.Matrix import Matrix
from playLA.Vector import Vector
from playLA.LinearSystem import LinearSystem
if __name__ == "__main__":
A = Matrix([[1, 2, 4], [3, 7, 2], [2, 3, 3]])
b = Vector([7, -11, 1])
ls = LinearSystem(A, b)
ls.gauss_jordan_elimination()
ls.fancy_print()
print()
A2 = Matrix([[1, -3, 5], [2, -1, -3], [3, 1, 4]])
b2 = Vector([-9, 19, -13])
ls2 = LinearSystem(A2, b2)
ls2.gauss_jordan_elimination()
ls2.fancy_print()
print()
A3 = Matrix([[1, 2, -2], [2, -3, 1], [3, -1, 3]])
b3 = Vector([6, -10, -16])
ls3 = LinearSystem(A3, b3)
ls3.gauss_jordan_elimination()
ls3.fancy_print()
print()
A4 = Matrix([[3, 1, -2], [5, -3, 10], [7, 4, 16]])
b4 = Vector([4, 32, 13])
ls4 = LinearSystem(A4, b4)
ls4.gauss_jordan_elimination()
ls4.fancy_print()
print()
A5 = Matrix([[6, -3, 2], [5, 1, 12], [8, 5, 1]])
b5 = Vector([31, 36, 11])
ls5 = LinearSystem(A5, b5)
ls5.gauss_jordan_elimination()
ls5.fancy_print()
print()
A6 = Matrix([[1, 1, 1], [1, -1, -1], [2, 1, 5]])
b6 = Vector([3, -1, 8])
ls6 = LinearSystem(A6, b6)
ls6.gauss_jordan_elimination()
ls6.fancy_print()
print()
A7 = Matrix([[1, -1, 2, 0, 3],
[-1, 1, 0, 2, -5],
[1, -1, 4, 2, 4],
[-2, 2, -5, -1, -3]])
b7 = Vector([1, 5, 13, -1])
ls7 = LinearSystem(A7, b7)
ls7.gauss_jordan_elimination()
ls7.fancy_print()
print()
A8 = Matrix([[2, 2],
[2, 1],
[1, 2]])
b8 = Vector([3, 2.5, 7])
ls8 = LinearSystem(A8, b8)
if not ls8.gauss_jordan_elimination():
print("No Solution!")
ls8.fancy_print()
print()
齐次线性方程组
等号右边全为0
所以最右行可以省略，解的过程可以只对系数矩阵做操作
image.png