Scalars,Vectors and Tensors

如果不想看英文请直接看下半部分的中文翻译。

scalar: a physical quantity that it represented by a dimensional number at a particular point in space and time. Examples are hydrostatic pressure and temperature.
vector: a bookkeeping tool to keep track of two pieces of information (typically magnitude and direction) for a physical quantity. Examples are position, force and velocity. The vector has three components.
Tensors: are geometric objects that describe linear relations between geometric vectors, scalars, and other tensors. Elementary examples of such relations include the dot product, the cross product, and linear maps. Geometric vectors, often used in physics and engineering applications, and scalars themselves are also tensors.[1]
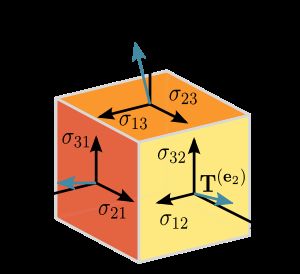
A more sophisticated example is the Cauchy stress tensorT, which takes a direction v as input and produces the stress T(v)
on the surface normal to this vector for output, thus expressing a relationship between these two vectors

Cauchy stress tensor

中文译文：
标量：在空间和时间的某一个特定的点上用一个维数表示的物理量。比如说静水压力和温度。
向量：用来记录两个信息--大小和方向的物理量。比如说是位置，压力和速度。下图中的速度有三个组成部分（速度在三维空间中的分解）

速度向量

上图中速度的大小是个标量v=| v|

张量: 用来描述在几何向量、标量或是其他张量之间的线性关系的一种几何学对象。这种线性关系包括点积、叉积和线性映射。几何向量，通常在工程或是物理学应用中使用。标量和向量本身就是张量的一种。 上面的图很好的解释了什么是Cauchy力的张量结构。每个面上都有一个力，每个力都可以分解到同一个坐标系上，所以就构成了一个张量。

标量是一个没有维度的实数（0维），向量是一个一维的数，再之后维度更高的数就用张量来表示了。