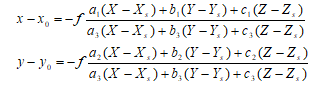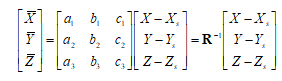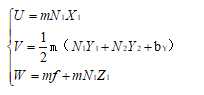相对定向-绝对定向（C++实现）--摄影测量学

一．目的

理解并掌握空间相对定向-原理。
体会相对定向-绝对定向与前后方交会的异同，理解各参数含义。
熟悉计算流程，并通过编程运用到实践上。
提高编程计算能力，并将算式转换为程序，体会编程计算的特点。

二．实验要求

提交实习报告：程序框图、程序源代码、计算结果、体会。
计算结果：相对定向五参数及精度评定、计算模型点坐标、绝对定向七参数及精度评定。

三．实验思路

先求解相对定向，解得五参数，然后计算模型点，最后求解七参数，求解地面摄影测量坐标。

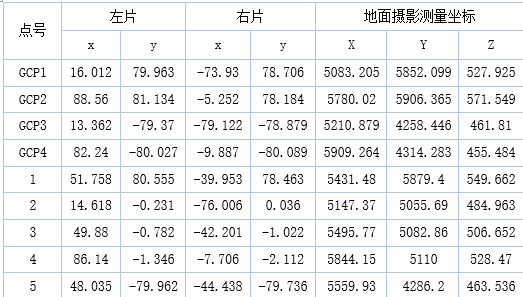
四．实验数据

点位信息。

点位信息

f=150.000mm，x0=0，y0=0

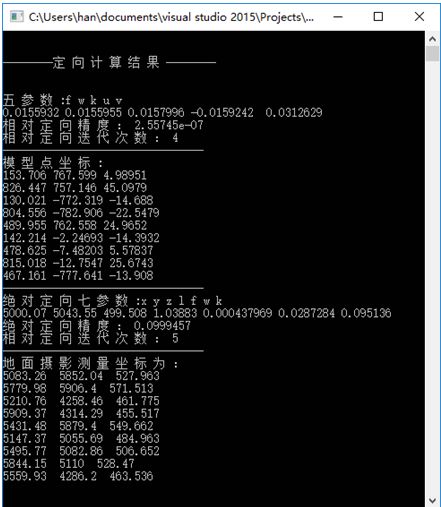
五．实验结果

待求点地面摄影测量坐标

结果
相对定向五参数

五参数 :f w k u v
0.0155932 0.0155955 0.0157996 -0.0159242 0.0312629
相对定向精度： 2.55745e-07
相对定向迭代次数： 4

模型点坐标

X Y Z
153.706 767.599 4.98951
826.447 757.146 45.0979
130.021 -772.319 -14.688
804.556 -782.906 -22.5479
489.955 762.558 24.9652
142.214 -2.24693 -14.3932
478.625 -7.48203 5.57837
815.018 -12.7547 25.6743
467.161 -777.641 -13.908

绝对定向七参数

绝对定向七参数 :x y z l f w k
5000.07 5043.55 499.508 1.03883 0.000437969 0.0287284 0.095136
绝对定向精度： 0.0999457
相对定向迭代次数： 5

地面摄影测量坐标

X Y Z
5083.26 5852.04 527.963
5779.98 5906.4 571.513
5210.76 4258.46 461.775
5909.37 4314.29 455.517
5431.48 5879.4 549.662
5147.37 5055.69 484.963
5495.77 5082.86 506.652
5844.15 5110 528.47
5559.93 4286.2 463.536

六．程序框图

相对定向

相对定向结果
模型点计算

模型点计算
绝对定向

绝对定向

七．实验原理公式

共线方程

共线方程
旋转矩阵

旋转矩阵
最小二乘准则

最小二乘准则
解析法相对定向原理：

根据同名光线对对相交这一立体像对内在的几何关系，通过量测的像点坐标，用解析计算的方法解求相对定向元素，建立与地面相似的立体模型，确定模型点的三维坐标。
相对定向的共面条件：B·（S1a1·S2a2）=0，即F=
连续像对的相对定向：连续像对法相对定向是以左像片为基准，求出右像片相对于左像片的五个定向元素 .为了统一单位，把bY，bZ两个基线元素改为角度形式表示，如下，μ和ν为极限的偏角和倾角。

前方交会

前方交会
模型点计算
绝对定向。

相对定向后建立的立体模型是相对于摄影测量坐标系统的，它在地面坐标系统中的方位是未知的，其比例尺也是任意的。如果想要知道模型中某点相应的地面点的地面坐标，就必须对所建立的模型进行绝对定向，即要确定模型在地面坐标系中的正确方位，及比例尺因子。很容易将模型坐标转化为地面坐标，这样就能确定出加密点的地面坐标。这叫立体模型的绝对定向。
绝对定向的定义：解算立体模型绝对方位元素的工作。立体模型绝对方位元素有7个，它们是：。
绝对定向的目的：恢复立体模型在地面坐标系中的大小和方位的工作。

八．实验代码（附录）

九．实验结果（截图）

十. 实验心得体会

一句话总结这次实验：收获甚丰，内心很苦。为何这样说？

首先说一下收获甚丰。这次实验真正的让我体会到相对定向-绝对定向与前后方交会之间的区别、联系。他们是空间双象解析的两种重要方法，但是求解思路却不相同。前后交会是先求解单张相片的地面摄影测量坐标，然后再前方交会实现还原相片位置，求解坐标；然而相对-绝对是先求解左右相片的相对位置，然后再逐步求解其在空间中的位置。两者相通的可能就是最基本的原理—共线方程，两者都采用前方交会计算坐标。因此，从根本上讲，前后方交会是同一问题的不同求解顺序。

其次想谈一谈内心的痛苦。说白了就是编程中所遇到的问题。

绝对定向中bx。
在求解过程中，bx = x1 – x2; 我开始写的是bx = x2 – x1；就是这样简单的问题，因为没有想清楚，所以就出错了。
相对定向中，bx其实是一个无关紧要的量，因此，我算出来相对定向的值是正确的；然而到了绝对定向，出现问题了，七参数中z异常打！然而找不到问题所在，最后在调试时，发现不对，才改正过来，于是乎，绝对定向才收敛，这个过程持续了至少5个小时。
数据录入错误。
这可能是最低级的错误，但是这次我又犯了，把一个数据的正负号搞错了，于是乎，根本不会闭合，看着迭代次数1，100，100…绝望！
矩阵与数组之间的频繁转换。
由于原始数据是数组，操作起来也很便捷，但有时候为了求逆，不得不将数据转为矩阵；有时候矩阵与数组结构不相同，出现了某一个位置未赋值的情况，从而出现各种奇怪的值！
参数过多，传值频繁。
此程序内的定向类可以认为根本不符合面向对象的编程思想，因为这个类的存在几乎就是为了在函数之间传递变量。因此，在数值传递过程中就会出现变量混乱，变量名污染的情况。
总之，这三天的编程还是蛮刺激的，不仅要一遍遍看书，还有详细了解编程知识，同时要不断地Debug，Debug，Debug……

附录

入口文件ResAblOrientation

#include "stdafx.h"
#include 
#include "Orientation.h"
using namespace std;
int main()
{
    //左片数据
    double l[9][2] = {
        { 0.016012 ,0.079963 },
        { 0.08856 ,0.081134 },
        { 0.013362 ,-0.07937 },
        { 0.08224 ,-0.080027 },
        { 0.051758,0.080555 },
        { 0.014618,-0.000231 },
        { 0.04988,-0.000782 },
        { 0.08614,-0.001346 },
        { 0.048035,-0.079962 }
    };
    //右片数据
    double r[9][2] = {
        { -0.07393,0.078706 },
        { -0.005252,0.078184 },
        { -0.079122,-0.078879 },
        { -0.009887,-0.080089 },
        { -0.039953,0.078463 },
        { -0.076006,0.000036 },
        { -0.042201,-0.001022 },
        { -0.007706,-0.002112 },
        { -0.044438,-0.079736 }
    };
    //控制点地面摄影测量坐标
    double g[4][3] = {
        { 5083.205,5852.099,527.925 },
        { 5780.02,5906.365,571.549 },
        { 5210.879,4258.446,461.81 },
        { 5909.264,4314.283,455.484 }
    };
    double f = 0.15; //焦距

    //实例化定向对象
    COrientation o(l,r,g,f);

    cout << endl << endl;
    cout << "--------定向计算结果--------" << endl;
    cout << endl << endl;
    //相对定向
    o.RelaOrientation();

    cout << "--------------------------------" << endl;

    //计算模型点
    o.ModelPoints();

    cout << "--------------------------------" << endl;

    //绝对定向
    o.AbsOrientation();

    cout << "--------------------------------" << endl;

    //计算坐标值
    o.GetPoints();

    cin.get();
    return 0;
}

定向类COrientation

#pragma once
#include "Matrix.h"
#include 
/*
定向类
*/
class COrientation
{
private:
    //相对定向五参数
    double f;
    double w;
    double k;
    double u;
    double v;
    double countx; //相对定向循环次数

    double df; //焦距
    double bx;
    double by;
    double bz;

    //七参数
    double x;
    double y;
    double z;
    double jf;
    double jw;
    double jk;
    double jl;
    double countj; //绝对定向循环次数

    double N1;
    double N2;

    double l[9][2]; //左片数据
    double r[9][2]; //右片数据
    double g[4][3]; //控制点地面摄影测量数据
    double p[9][3]; //模型点数据

public:
    //初始化
    COrientation(double l[9][2], double r[9][2], double g[4][3],double f);
    void RelaOrientation(); //相对定向
    void ModelPoints(); //计算模型点
    void AbsOrientation(); //绝对定向
    void GetPoints(); //得出地面摄影测量坐标
    CMatrix GetR(double f, double w, double k); //计算旋转矩阵
    ~COrientation();
};

#include "stdafx.h"
#include "Orientation.h"
#include "math.h"
#include 
using namespace std;
COrientation::COrientation(double lpoints[9][2], double rpoints[9][2], double g[4][3], double df)
{
    //焦距
    this->df = df;
    //初始值
    bx = lpoints[0][0] - rpoints[0][0]; //bx初始值
    //初始值
    f = w = k = u = v = 0;
    countx = countj = 0;
    //赋值
    for (int i = 0; i < 9; i++)
    {
        for (int j = 0; j < 2; j++)
        {
            l[i][j] = lpoints[i][j];
            r[i][j] = rpoints[i][j];
        }
    }
    for (int i = 0; i < 4; i++)
    {
        for (int j = 0; j < 3; j++)
        {
            this->g[i][j] = g[i][j];
        }
    }
}

void COrientation::RelaOrientation()
{
    //误差方程参数
    CMatrix A(6, 5), L(6, 1), X(5, 1), V(6, 1);

    //右片相对相空间坐标，相对摄影测量坐标
    CMatrix mr(3, 1), mrimg(3, 1);

    //迭代运算
    while (1)
    {
        //计算旋转矩阵
        CMatrix R2 = GetR(f, w, k);

        //by,bz计算
        by = bx*u;
        bz = bx*v;

        //计算每个点参数，组成法方程矩阵
        for (int i = 0; i < 6; i++)
        {
            //左片相对摄影测量坐标
            double x1 = l[i][0];
            double y1 = l[i][1];
            double z1 = -df;

            //右片相对摄影测量坐标
            mr(0, 0) = r[i][0];
            mr(1, 0) = r[i][1];
            mr(2, 0) = -df;
            //计算相对摄影测量坐标
            mrimg = R2*mr;

            //计算N1，N2
            N1 = (bx*mrimg(2, 0)- bz*mrimg(0, 0)) / (x1*mrimg(2, 0) - mrimg(0, 0)*z1);
            N2 = (bx*z1 - bz*x1) / (x1*mrimg(2, 0) - mrimg(0, 0)*z1);
            //计算每个点的Q值
            double Q = N1*y1 - N2*mrimg(1, 0) - by;
            //计算每个点误差系数
            double v[5] = {0};
            v[0] = -mrimg(0, 0)*mrimg(1, 0)*N2 / mrimg(2, 0);
            v[1] = -(mrimg(2, 0) + mrimg(1, 0)*mrimg(1, 0) / mrimg(2, 0))*N2;
            v[2] = mrimg(0, 0)*N2;
            v[3] = bx;
            v[4] = -mrimg(1, 0)*bx / mrimg(2, 0);

            //加入总误差系数阵
            for (int ii = 0; ii < 5; ii++)
                A(i, ii) = v[ii];
            L(i, 0) = Q;
        }
        //求解X
        X = (~A*A).Inv()*(~A)*L;

        //累加五参数
        f += X(0, 0);
        w += X(1, 0);
        k += X(2, 0);
        u += X(3, 0);
        v += X(4, 0);

        //循环次数＋
        countx++;

        //判断是否收敛
        if (abs(X(0, 0)) < 0.00003 && abs(X(1, 0)) < 0.00003 && abs(X(2, 0)) < 0.00003 && abs(X(3, 0)) < 0.00003 && abs(X(4, 0)) < 0.00003)
        {
            //输出五参数
            cout << "五参数:f w k u v" << endl;
            cout << f << " " << w << " " << k << " " << u << "  " << v << endl;
            //评定精度
            V = A*X - L;
            double c1 = sqrt((~V*V)(0, 0) / 6);
            cout << "相对定向精度：" << c1 << endl;
            cout << "相对定向迭代次数：" << countx << endl;
            break;
        }
    }


}

void COrientation::ModelPoints()
{
    //比例尺
    double m1 = sqrt((l[0][0] - l[1][0])*(l[0][0] - l[1][0]) + (l[0][1] - l[1][1])*(l[0][1] - l[1][1]));
    double m2 = sqrt((g[0][0] - g[1][0])*(g[0][0] - g[1][0]) + (g[0][1] - g[1][1])*(g[0][1] - g[1][1]));
    double m = m2 / m1;
    //m = 10000;

    //计算每个点模型坐标
    //右片相对相空间坐标，相对摄影测量坐标
    CMatrix mr(3, 1), mrimg(3, 1);
    //计算旋转矩阵
    CMatrix R2 = GetR(f, w, k);
    for (int i = 0; i < 9; i++)
    {

        //左片相对摄影测量坐标
        double x1 = l[i][0];
        double y1 = l[i][1];
        double z1 = -df;

        //右片相对摄影测量坐标
        mr(0, 0) = r[i][0];
        mr(1, 0) = r[i][1];
        mr(2, 0) = -df;
        //计算相对摄影测量坐标
        mrimg = R2*mr;

        //计算N1，N2
        N1 = (bx*mrimg(2, 0) - bz*mrimg(0, 0)) / (x1*mrimg(2, 0) - mrimg(0, 0)*z1);
        N2 = (bx*z1 - bz*x1) / (x1*mrimg(2, 0) - mrimg(0, 0)*z1);

        double xp = m*N1*x1;
        double yp = 0.5*m*(N1*y1 + N2*mrimg(1, 0) + by);
        double zp = m*df + m* N1*(-df);
        p[i][0] = xp;
        p[i][1] = yp;
        p[i][2] = zp;
    }
    cout << "模型点坐标:" << endl;
    for (int i = 0; i < 9; i++)
    {
        for (int j = 0; j < 3; j++)
            cout << p[i][j] << " ";
        cout << endl;
    }
}

void COrientation::AbsOrientation()
{
    //初始化七参数
    x = y = z = jf = jw = jk = 0;
    jl = 1;
    //法方程系数
    CMatrix A(12, 7), L(12, 1), V(12, 1), X(7,1);
    //迭代计算
    while (true)
    {
        //计算每一个点的系数
        for (int i = 0; i < 4; i++)
        {
            //旋转矩阵
            CMatrix R = GetR(jf, jw, jk);
            //每个点误差方程系数
            CMatrix mtp(3, 1), mp(3, 1), p0(3, 1);
            //赋值给矩阵，便于计算
            for (int j = 0; j < 3; j++)
            {
                mtp(j, 0) = g[i][j];
                mp(j, 0) = p[i][j];
            }
            p0(0, 0) = x;
            p0(1, 0) = y;
            p0(2, 0) = z;
            //计算每个点的L
            CMatrix jL = mtp - jl*R*mp - p0;
            //每个点3X3的系数阵A
            CMatrix jA(3, 7);
            jA(0, 0) = 1;
            jA(1, 1) = 1;
            jA(2, 2) = 1;
            jA(0, 3) = p[i][0];
            jA(0, 4) = -p[i][2];
            jA(0, 6) = -p[i][1];
            jA(1, 3) = p[i][1];
            jA(1, 5) = -p[i][2];
            jA(1, 6) = p[i][0];
            jA(2, 3) = p[i][2];
            jA(2, 4) = p[i][0];
            jA(2, 5) = p[i][1];

            //添加到大系数阵A,L
            for (int j = 0; j < 7; j++)
            {
                A(3 * i, j) = jA(0, j);
                A(3 * i + 1, j) = jA(1, j);
                A(3 * i + 2, j) = jA(2, j);
            }
            L(3 * i, 0) = jL(0, 0);
            L(3 * i + 1, 0) = jL(1, 0);
            L(3 * i + 2, 0) = jL(2, 0);
        }

        //求解法方程
        X = (~A*A).Inv()*~A*L;

        //累加七参数
        x += X(0, 0);
        y += X(1, 0);
        z += X(2, 0);
        jl += X(3, 0);
        jf += X(4, 0);
        jw += X(5, 0);
        jk += X(6, 0);

        //循环次数累加
        countj++;
        //判断是否收敛
        if (abs(X(0, 0)) < 0.001 && abs(X(1, 0)) < 0.001 && abs(X(2, 0)) < 0.001 && abs(X(3, 0)) < 0.001 && abs(X(4, 0)) < 0.001&& abs(X(5, 0)) < 0.001 && abs(X(6, 0)) < 0.001)
        {
            cout << "绝对定向七参数:x y z l f w k" << endl;;
            cout << x << " " << y << " " << z << " " << jl << " " << jf << " " << jw << " " << jk << endl;;
            //精度评定
            V = A*X - L;
            double c2 = sqrt((~V*V)(0, 0) / 4);
            cout << "绝对定向精度：" << c2 << endl;
            cout << "相对定向迭代次数：" << countj << endl;
            break;
        }
    }

}

void COrientation::GetPoints()
{
    CMatrix XTP(9,3); //地面摄影测量坐标
    //计算坐标
    for (int i = 0; i < 9; i++)
    {
        //依次为相对摄影测量坐标、七参数、地面摄影测量坐标
        CMatrix XP(3, 1), DX(3, 1), mXTP(3, 1);
        //为矩阵赋值
        XP(0, 0) = p[i][0]; 
        XP(1, 0) = p[i][1]; 
        XP(2, 0) = p[i][2];

        DX(0, 0) = x; 
        DX(1, 0) = y, 
        DX(2, 0) = z;
        //计算摄影测量坐标
        mXTP = jl*GetR(jf, jw, jk)*XP + DX;
        for (int j = 0; j < 3; j++)
        {
            XTP(i, j) = mXTP(j, 0);
        }
    }
    cout << "地面摄影测量坐标为：" << endl;
    cout << XTP;
}

CMatrix COrientation::GetR(double f, double w, double k)
{
    CMatrix R2(3, 3);
    R2(0, 0) = cos(f)*cos(k) - sin(f)*sin(w)*sin(k);
    R2(0, 1) = -cos(f)*sin(k) - sin(f)*sin(w)*cos(k);
    R2(0, 2) = -sin(f)*cos(w);
    R2(1, 0) = cos(w)*sin(k);
    R2(1, 1) = cos(w)*cos(k);
    R2(1, 2) = -sin(w);
    R2(2, 0) = sin(f)*cos(k) + cos(f)*sin(w)*sin(k);
    R2(2, 1) = -sin(f)*sin(k) + cos(f)*sin(w)*cos(k);
    R2(2, 2) = cos(f)*cos(w);

    return R2;
}

COrientation::~COrientation()
{
}

矩阵类CMatrix

#pragma once
#include 
using namespace std;
class CMatrix
{
public:
    CMatrix(int row = 3, int col = 3);
    // copy constructor

    CMatrix(const CMatrix& m);


    ~CMatrix(void);
private:
    double **dMatData;//保存矩阵元素数据的二维数组
    int iRow;//矩阵的行
    int iCol;//矩阵的列

public:
    int Row() const { return iRow; }//返回行
    int Col() const { return iCol; }//返回列
    void SetSize(int row, int col);//调整数组的大小，原有数据不变（未测试）
    void SetRow(int row, double arrrow[]); //设置一行元素

    double& operator () (int row, int col);//获取矩阵元素
    double  operator () (int row, int col) const;//重载获取矩阵元素函数，只有const对象能访问

    CMatrix& operator = (const CMatrix& m);

    //注意：友元函数并不是类自己的成员函数
    friend CMatrix operator + (const CMatrix& m1, const CMatrix& m2);
    friend CMatrix operator - (const CMatrix& m1, const CMatrix& m2);
    friend CMatrix operator * (const CMatrix& m1, const CMatrix& m2);
    friend CMatrix operator * (const double& num, const CMatrix& m1);
    friend CMatrix operator * (const CMatrix& m1, const double& num);
    friend ostream & operator<<(ostream &out, CMatrix &m); //重载<<

    friend CMatrix operator ~ (const CMatrix& m);//矩阵转置
    CMatrix Inv();//矩阵求逆
    void Unit();//生成单位矩阵
};


#include "stdafx.h"
#include "Matrix.h"
#include "math.h"

CMatrix::CMatrix(int row, int col)
{
    iRow = row;
    iCol = col;
    dMatData = new double*[row];

    for (int i = 0; i < row; i++)
    {
        dMatData[i] = new double[col];
        for (int j = 0; j= iRow || col >= iCol)
    {
        throw("CMatrix::operator(): Index out of range!");
    }

    return dMatData[row][col];
}

////返回数组元素（重载）
double CMatrix::operator () (int row, int col) const
{
    if (row >= iRow || col >= iCol)
    {
        throw("CMatrix::operator(): Index out of range!");
    }

    return dMatData[row][col];
}


//重载预算符+
CMatrix operator + (const CMatrix& m1, const CMatrix& m2)
{

    if ((m1.Col() != m2.Col()) || (m1.Row() != m2.Row()))
    {
        throw("CMatrix::operator+: The two matrix have different size!");
    }

    CMatrix matTmp(m1.Row(), m1.Col());
    for (int i = 0; irow) ? row : iRow;
    int minCol = (iCol>col) ? col : iCol;
    int  colSize = minCol * sizeof(double);


    for (int i = 0; i < minRow; i++)
    {
        memcpy(rsData[i], dMatData[i], colSize);
    }

    for (int i = 0; i < minRow; i++)
    {
        delete[] dMatData[i];
    }
    delete[] dMatData;
    dMatData = rsData;
    iRow = row;
    iCol = col;
    return;
}
void CMatrix::SetRow(int row, double arrrow[])
{
    if (row > iRow)
        throw("CMatrix::SetRow: the row is out of index");
    if (sizeof(arrrow) / sizeof(double) > iCol)
        throw("CMatrix::SetRow: the col is out of index");
    for (int i = 0; i < iCol; i++)
    {
        dMatData[row][i] = arrrow[i];
    }
}



//重载预算符-
CMatrix operator - (const CMatrix& m1, const CMatrix& m2)
{

    if ((m1.Col() != m2.Col()) || (m1.Row() != m2.Row()))
    {
        throw("CMatrix::operator-: The two matrix have different size!");
    }

    CMatrix matTmp(m1.Row(), m1.Col());
    for (int i = 0; i dMainCell)
                {
                    dMainCell = dTemp;
                    MainRow[k] = i;
                    MainCol[k] = j;
                }
            }
        }

        if (fabs(dMainCell) < 0.0000000000001)//矩阵秩亏，不能求逆
        {
            throw("矩阵秩亏");
        }

        if (MainRow[k] != k)//交换行
        {
            for (j = 0; j= 0; k--)
    {
        if (MainCol[k] != k)// 交换行
        {
            for (j = 0; j

相对定向-绝对定向（C++实现）--摄影测量学

一． 目的

二． 实验要求

三． 实验思路