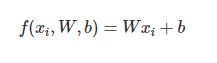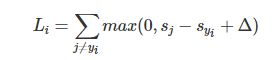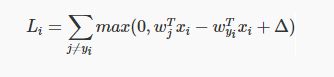前言:
以斯坦福cs231n课程的python编程任务为主线,展开对该课程主要内容的理解和部分数学推导。
该课程相关笔记参考自知乎-CS231n官方笔记授权翻译总集篇发布
课程材料和事例参考自-cs231n
SVM分类器简介:
SVM-支持向量机(Support Vector Machine),是一个有监督的线性分类器
线性分类器:在本模型中,我们从最简单的函数开始,一个线性映射:
这个公式就是平时最常见到的线性函数,常为一维线性函数(即 W 为一维的)。当这种函数扩展到多维度的情况下时就是我们SVM要面临的情况。首先我们要做的处理是将每个图像数据都拉长为一个长度为D的列向量,大小为 [D * 1] 。其中大小为 [K * D] 的矩阵W和大小为 [K 1] 列向量 b 为该函数的参数。以CIFAR-10为例,CIFAR-10中一个图像的大小等于 [32323] ,含了该图像的所有像素信息,这些信息被拉成为一个 [3072 * 1] 的列向量, W 大小为 [103072] , b 的大小为 [10*1] 。因此,3072个数字(素数值)输入函数,函数输出10个数字(不同分类得到的评分)。参数 W 被称为权重(weights)。 b 被称为偏差向量(bias vector)。
理解线性分类器
线性分类器计算图像中3个颜色通道中所有像素的值与权重的矩阵乘,从而得到分类分值。根据我们对权重设置的值,对于图像中的某些位置的某些颜色,函数表现出的得分即对该点的接受程度。例如对于飞机来说,飞机图片中包含有大量的蓝色天空,白色的云彩以及白色的飞机,那么这个飞机分类器就会在蓝色通道上的权重比较多,而在其他通道上的权重就较少,正如笔记中指出的:
一个将图像映射到分类分值的例子。为了便于可视化,假设图像只有4个像素(都是黑白像素,这里不考虑RGB通道),有3个分类(红色代表猫,绿色代表狗,蓝色代表船,注意,这里的红、绿和蓝3种颜色仅代表分类,和RGB通道没有关系)。首先将图像像素拉伸为一个列向量,与W进行矩阵乘,然后得到各个分类的分值。需要注意的是,这个W一点也不好:猫分类的分值非常低。从上图来看,算法倒是觉得这个图像是一只狗。
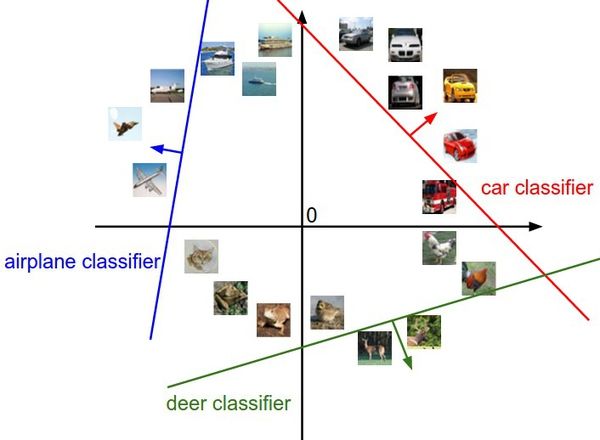
现在考虑高维度情况:还是以CIFAR-10为例,CIFAR-10中的图片转化成一个向量(3072维)后,就是一个高维度问题,而一个向量(3色通道转化而来)可以看作是3072维空间中的一个点,而线性分类器就是在高维度空间中的一个超平面,将各个空间点分开。如图所示:
图像空间的示意图。其中每个图像是一个点,有3个分类器。以红色的汽车分类器为例,红线表示空间中汽车分类分数为0的点的集合,红色的箭头表示分值上升的方向。所有红线右边的点的分数值均为正,且线性升高。红线左边的点分值为负,且线性降低。
目标:而我们要做的就是寻找一个W和一个b,使得这个超平面能很好的区分各个类。寻找方法就是不停的改变w和b的值,即不停的旋转平移,直到它使分类的偏差较小。
SVM的组成:
这个函数得到的就是当前分类的偏差值。
举例:用一个例子演示公式是如何计算的。假设有3个分类,并且得到了分值s=[13,-7,11]。其中第一个类别是正确类别,即$y_i=0$。同时假设$\Delta$是10。上面的公式是将所有不正确分类加起来,所以得到两个部分:
$$Li=max(0,-7-13+10)+max(0,11-13+10)$$
可以看到第一个部分结果是0,这是因为[-7-13+10]得到的是负数,经过函数处理后得到0。这一对类别分数和标签的损失值是0,这是因为正确分类的得分13与错误分类的得分-7的差为20,高于边界值10。而SVM只关心差距至少要大于10,更大的差值还是算作损失值为0。第二个部分计算[11-13+10]得到8。虽然正确分类的得分比不正确分类的得分要高(13>11),但是比10的边界值还是小了,分差只有2,这就是为什么损失值等于8。简而言之,SVM的损失函数想要正确分类类别的分数比不正确类别分数高,而且至少要高。如果不满足这点,就开始计算损失值。
那么在这次的模型中,我们面对的是线性评分函数(f(x_i,W)=Wx_i),所以我们可以将损失函数的公式稍微改写一下:
其中w_j是权重W的第j行,被变形为列向量。然而,一旦开始考虑更复杂的评分函数f公式,这样做就不是必须的了。
一个简单的例子:如果W能够正确分类所有数据,即对于每个数据,损失值都是0。那么当时,任何数乘都能使得损失值为0,因为这个变化将所有分值的大小都均等地扩大了,所以它们之间的绝对差值也扩大了。举个例子,如果一个正确分类的分值和举例它最近的错误分类的分值的差距是15,对W乘以2将使得差距变成30。
当然,在没有这种模糊性的情况下我们能很好的控制偏差。而减少这种模糊性的方法是向损失函数增加一个正则化惩罚(regularization penalty)部分。最常用的正则化惩罚是L2范式,L2范式通过对所有参数进行逐元素的平方惩罚来抑制大数值的权重,将其展开完整公式是:
其中,N是训练集的数据量。现在正则化惩罚添加到了损失函数里面,并用超参数来计算其权重。该超参数无法简单确定,需要通过交叉验证来获取,引入了L2惩罚后,SVM们就有了最大边界这一良好性质。(如果感兴趣,可以查看CS229课程)。
SVM实现:
#coding:utf-8
import numpy as np
from random import shuffle
def svm_loss_naive(W, X, y, reg):
"""
Structured SVM loss function, naive implementation (with loops).
Inputs have dimension D, there are C classes, and we operate on minibatches
of N examples.
Inputs:
- W: A numpy array of shape (D, C) containing weights.
- X: A numpy array of shape (N, D) containing a minibatch of data.
- y: A numpy array of shape (N,) containing training labels; y[i] = c means
that X[i] has label c, where 0 <= c < C.
- reg: (float) regularization strength
Returns a tuple of:
- loss as single float
- gradient with respect to weights W; an array of same shape as W
"""
dW = np.zeros(W.shape) # initialize the gradient as zero
# compute the loss and the gradient
num_classes = W.shape[1]
num_train = X.shape[0]
loss = 0.0
for i in xrange(num_train):
scores = X[i].dot(W)
correct_class_score = scores[y[i]]
for j in xrange(num_classes):
if j == y[i]:
continue
margin = scores[j] - correct_class_score + 1 # note delta = 1
if margin > 0:
loss += margin
dW[:, y[i]] += -X[i, :]
dW[:, j] += X[i, :]
# Right now the loss is a sum over all training examples, but we want it
# to be an average instead so we divide by num_train.
loss /= num_train
dW /= num_train
# Add regularization to the loss.
loss += reg * np.sum(W * W)
dW += reg * W
return loss, dW
def svm_loss_vectorized(W, X, y, reg):
"""
Structured SVM loss function, vectorized implementation.
Inputs and outputs are the same as svm_loss_naive.
"""
loss = 0.0
dW = np.zeros(W.shape) # initialize the gradient as zero
scores = X.dot(W)
num_classes = W.shape[1]
num_train = X.shape[0]
scores_correct = scores[np.arange(num_train), y] # 1 by N
scores_correct = np.reshape(scores_correct, (num_train, -1)) # N by 1
margins = scores - scores_correct + 1 # N by C
margins = np.maximum(0,margins)
margins[np.arange(num_train), y] = 0
loss += np.sum(margins) / num_train
loss += 0.5 * reg * np.sum(W * W)
# compute the gradient
margins[margins > 0] = 1
row_sum = np.sum(margins, axis=1) # 1 by N
margins[np.arange(num_train), y] = -row_sum
dW += np.dot(X.T, margins)/num_train + reg * W # D by C
return loss, dW
#coding:utf-8
import numpy as np
from classifiers.linear_svm import *
from classifiers.softmax import *
class LinearClassifier(object):
def __init__(self,w=None):
self.W = w
def train(self, X, y, learning_rate=1e-3, reg=1e-5, num_iters=100,
batch_size=200, verbose=False):
"""
Train this linear classifier using stochastic gradient descent.
Inputs:
- X: A numpy array of shape (N, D) containing training data; there are N
training samples each of dimension D.
- y: A numpy array of shape (N,) containing training labels; y[i] = c
means that X[i] has label 0 <= c < C for C classes.
- learning_rate: (float) learning rate for optimization.
- reg: (float) regularization strength.
- num_iters: (integer) number of steps to take when optimizing
- batch_size: (integer) number of training examples to use at each step.
- verbose: (boolean) If true, print progress during optimization.
Outputs:
A list containing the value of the loss function at each training iteration.
"""
num_train, dim = X.shape
num_classes = np.max(y) + 1 # assume y takes values 0...K-1 where K is number of classes
if self.W is None:
# lazily initialize W
self.W = 0.001 * np.random.randn(dim, num_classes)
# Run stochastic gradient descent to optimize W
loss_history = []
for it in xrange(num_iters):
X_batch = None
y_batch = None
sample_index = np.random.choice(num_train, batch_size, replace=False)
X_batch = X[sample_index, :] # select the batch sample
y_batch = y[sample_index] # select the batch label
# evaluate loss and gradient
loss, grad = self.loss(X_batch, y_batch, reg)
loss_history.append(loss)
# perform parameter update
self.W += -learning_rate * grad
if verbose and it % 100 == 0:
print 'iteration %d / %d: loss %f' % (it, num_iters, loss)
return loss_history
def predict(self, X):
"""
Use the trained weights of this linear classifier to predict labels for
data points.
Inputs:
- X: D x N array of training data. Each column is a D-dimensional point.
Returns:
- y_pred: Predicted labels for the data in X. y_pred is a 1-dimensional
array of length N, and each element is an integer giving the predicted
class.
"""
y_pred = np.zeros(X.shape[1])
score = X.dot(self.W)
y_pred = np.argmax(score,axis=1)
return y_pred
def loss(self, X_batch, y_batch, reg):
"""
Compute the loss function and its derivative.
Subclasses will override this.
Inputs:
- X_batch: A numpy array of shape (N, D) containing a minibatch of N
data points; each point has dimension D.
- y_batch: A numpy array of shape (N,) containing labels for the minibatch.
- reg: (float) regularization strength.
Returns: A tuple containing:
- loss as a single float
- gradient with respect to self.W; an array of the same shape as W
"""
pass
class LinearSVM(LinearClassifier):
""" A subclass that uses the Multiclass SVM loss function """
def loss(self, X_batch, y_batch, reg):
return svm_loss_vectorized(self.W, X_batch, y_batch, reg)
class Softmax(LinearClassifier):
""" A subclass that uses the Softmax + Cross-entropy loss function """
def loss(self, X_batch, y_batch, reg):
return softmax_loss_vectorized(self.W, X_batch, y_batch, reg)
测试:
不同参数下SVM10类分类的准确率如下:
总结:
SVM在分类少以及线性的情况下有非常好的分类效果(尤其是二类),在配合PCA的情况下会有更好的结果。