本文旨在探索泰坦尼克号乘客的生存率的影响因素,全文分为三大部分:
一、数据概况;
二、数据探索;
三、结论;
一、数据概况;
# 引入必要的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%pylab inline
# 导入csv文件的数据,并查看
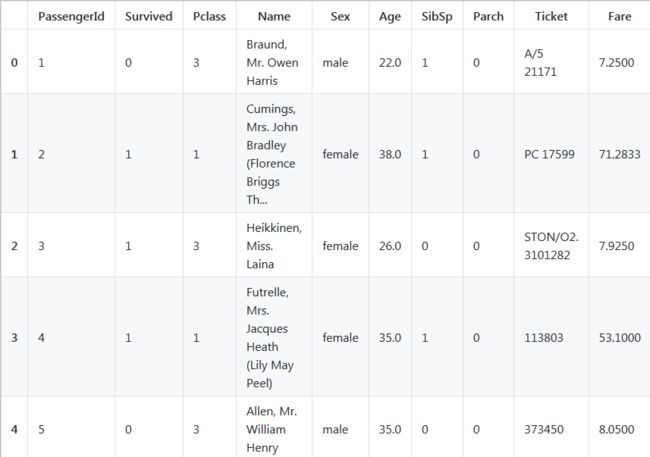
titanic_df = pd.read_csv('titanic-data.csv')
titanic_df.head()
Populating the interactive namespace from numpy and matplotlib
# 查看数据的基本信息
titanic_df.info()
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
PassengerId 891 non-null int64
Survived 891 non-null int64
Pclass 891 non-null int64
Name 891 non-null object
Sex 891 non-null object
Age 714 non-null float64
SibSp 891 non-null int64
Parch 891 non-null int64
Ticket 891 non-null object
Fare 891 non-null float64
Cabin 204 non-null object
Embarked 889 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.6+ KB
# 先简单看下数据的基本统计学信息;
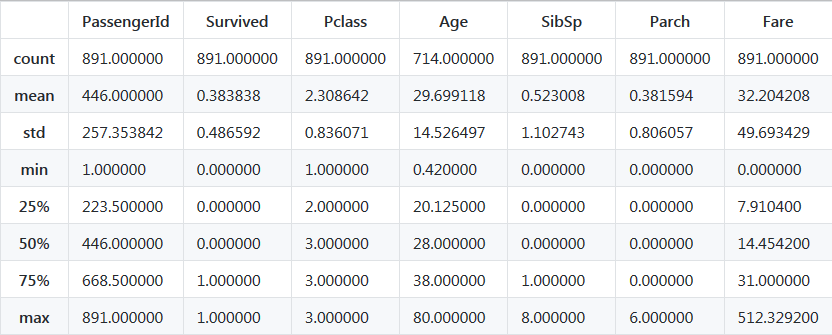
titanic_df.describe()
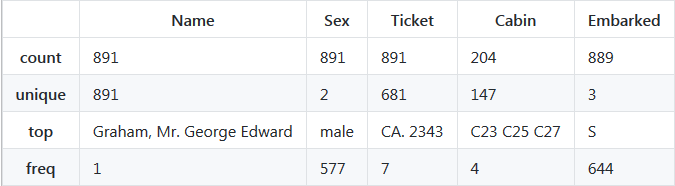
titanic_df.describe(include=['O'])
可以找出几个有用的信息:
- 乘客平均的生存率为0.38;
- 大部分数据有891个,较为齐全;
- 年龄 和 登船港口 信息缺失,如需研究需要补齐;
二、数据探索
有4个初步的想法,文章从4个方面探索:
- 妇女更有可能生存;
- 儿童更有可能生存;
- 上层乘客更有可能生存;
- 一些新想法
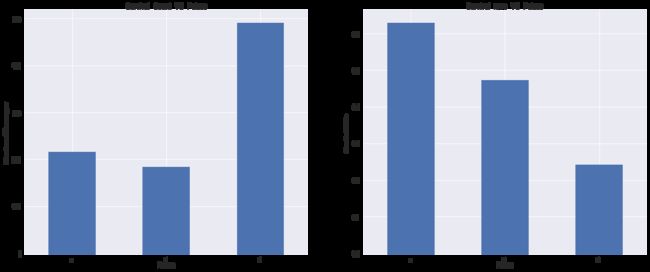
1.性别对生存率的影响
(1)左图:不同性别(男 or 女)人口数量分布图:
男女比例大概为2:1,有统计意义;
(2)右图:不同性别的存活率图;
plt.figure(figsize = (14, 5))
f, (ax1, ax2) = plt.subplots(1, 2)
ax1.set_title('Survival Count VS Sex')
ax1.set_ylabel('Number of Passenger')
ax2.set_title('Survival rage VS Sex')
ax2.set_ylabel('Survival Rate')
f.set_size_inches((20, 8))
titanic_df.groupby('Sex', as_index=False)['Survived'].count().plot(kind = 'bar', ax = ax1)
titanic_df.groupby('Sex', as_index=False)['Survived'].mean().plot(kind = 'bar', ax = ax2)
1.png
女人的生存率为0.74,男人生存率为0.18,差别非常大;
小结:
女士更有可能生还
2. 年龄对生存率的影响
(1)缺失值填充:
年龄age有714个,正常有891个,需要处理缺失值,这里采用的方法是用平均值填充;
# 计算平均年龄
titanic_age_mean = titanic_df['Age'].mean()
# 填充缺失值nan为平均值
titanic_df["Age"] = titanic_df["Age"].fillna(titanic_age_mean)
# 转换年龄的格式从float 到 int
titanic_df['Age'] = titanic_df['Age'].astype(int)
(2)各年龄段生还率研究:
- 为了方便分析,将年龄这种连续变量转化为分类变量;
- 创建一个年龄段变量,比如(0, 10], (10, 20]......然后对乘客根据年龄分组;
- 查看每个年龄段的乘客数量、生还率;
# 生成一个年龄段list
bins = np.arange(0, 90, 10)
# 新建Age_group变量为年龄段
titanic_df['Age_group'] = pd.cut(titanic_df['Age'], bins)
plt.figure(figsize = (14, 5))
f, (ax1, ax2) = plt.subplots(1, 2)
ax1.set_title('Survival Count VS Age')
ax1.set_ylabel('Number of Passenger')
ax2.set_title('Survival rage VS Age')
ax2.set_ylabel('Survival Rate')
f.set_size_inches((20, 8))
titanic_df.groupby('Age_group')['Survived'].count().plot(kind = 'bar', ax = ax1)
titanic_df.groupby('Age_group')['Survived'].mean().plot(kind = 'bar', ax = ax2)
从上图可以看出,在大概0-10岁的儿童,其生还的概率超过50%,超过其他年龄段;
小结:
儿童更有可能生还;
3.乘客所在船层对生存率的影响
(1)左图:不同船层乘客数量柱状图;
(2)右图:不同船层乘客生存率柱状图;
plt.figure(figsize = (14, 5))
f, (ax1, ax2) = plt.subplots(1, 2)
ax1.set_title('Survival Count VS Pclass')
ax1.set_ylabel('Number of Passenger')
ax2.set_title('Survival rage VS Pclass')
ax2.set_ylabel('Survival Rate')
f.set_size_inches((20, 8))
titanic_df.groupby('Pclass')['Survived'].count().plot(kind = 'bar', ax = ax1)
titanic_df.groupby('Pclass')['Survived'].mean().plot(kind = 'bar', ax = ax2)
不同船层的乘客生存率有显著差异:
- Pclass为1,即在 船上层 的乘客生存率为0.63;
- Pclass为2,即在 船中层 的乘客生存率为0.47;
- Pclass为3,即在 船底层 的乘客生存率为0.24;
小结:
** 上层乘客更有可能生存**
4.一些新想法
既然性别,船层对生还率都有影响,那么她们的组合因素有没有影响呢,
所以做了以下探究:
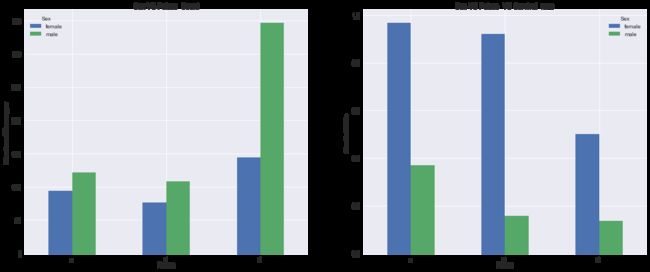
左图:不同性别、船层 的乘客数量图形
右图:不同性别,船层 的乘客生还率图形
plt.figure(figsize(14, 5))
f, (ax1, ax2) = plt.subplots(1,2)
ax1.set_title('Sex VS Pclass Count')
ax1.set_ylabel('Number of Passenger')
ax2.set_title('Sex VS Pclass VS Survival rage')
ax2.set_ylabel('Survival Rate')
f.set_size_inches((20, 8))
titanic_df.groupby(['Pclass', 'Sex'])['Survived'].count().unstack().plot(kind = 'bar', ax = ax1)
titanic_df.groupby(['Pclass', 'Sex'])['Survived'].mean().unstack().plot(kind = 'bar', ax = ax2)
可以看出,船上层 和 中层的女生绝大多数都存活下来,
且整体看 存活率由高到低依次是:
(1.female) > (2,female) > (3,female) > (1,male) > (2,male) > (3,male)
小结:
无论是男性还是女性,存活率都随着pclass的增加而降低;
三、结论:
- 本报告所用乘客数据集为891名,实际乘客为2224名,样本占总量的40.1%,可以代表整个整体,结论仍有可能有偏差,但是分析结果在统计学上可以认为是正确的;
- 对年龄缺失值采用平均值替代的处理可能会造成偏差,关于年龄部分的结论还需要再探究寻找更加合理的方式;
- 个人认为还有其他影响存活率的因素,比如:职业,地区,收入等;
- 真实的影响因素是多样且互相关联的,本文得出的所有结论只是很简单的分析某些变量与生存率的关系,一家之言,欢迎交流;