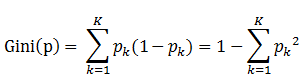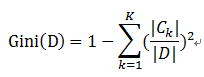1.随机森林回归和分类的不同:
随机森林可以应用在分类和回归问题上。实现这一点,取决于随机森林的每颗cart树是分类树还是回归树。
如果cart树是分类数,那么采用的计算原则就是gini指数。随机森林基于每棵树的分类结果,采用多数表决的手段进行分类。
基尼指数( CART算法 —分类树)
定义:基尼指数(基尼不纯度):表示在样本集合中一个随机选中的样本被分错的概率。Gini指数越小表示集合中被选中的样本被分错的概率越小,也就是说集合的纯度越高,反之,集合越不纯。
即 基尼指数(基尼不纯度)= 样本被选中的概率 * 样本被分错的概率
说明:
pk表示选中的样本属于k类别的概率,则这个样本被分错的概率是(1-pk)
样本集合中有K个类别,一个随机选中的样本可以属于这k个类别中的任意一个,因而对类别就加和
当为二分类是,Gini(P) = 2p(1-p)
样本集合D的Gini指数 : 假设集合中有K个类别,则:
如果是回归树,则cart树是回归树,采用的原则是最小均方差。即对于任意划分特征A,对应的任意划分点s两边划分成的数据集D1和D2,求出使D1和D2各自集合的均方差最小,同时D1和D2的均方差之和最小所对应的特征和特征值划分点。表达式为:
minA,s[minc1∑xi∈D1(A,s)(yi−c1)2+minc2∑xi∈D2(A,s)(yi−c2)2]
其中,c1为D1数据集的样本输出均值,c2为D2数据集的样本输出均值。
cart树的预测是根据叶子结点的均值,因此随机森林的预测是所有树的预测值的平均值。
补充:CART分类树算法对于连续特征和离散特征处理的改进
对于CART分类树连续值的处理问题,其思想和C4.5是相同的,都是将连续的特征离散化。唯一的区别在于在选择划分点时的度量方式不同,C4.5使用的是信息增益,则CART分类树使用的是基尼系数。
具体的思路如下,比如m个样本的连续特征A有m个,从小到大排列为a1,a2,…,am,则CART算法取相邻两样本值的中位数,一共取得m-1个划分点,其中第i个划分点表示Ti表示为:Ti=ai+ai+12。对于这m-1个点,分别计算以该点作为二元分类点时的基尼系数。选择基尼系数最小的点作为该连续特征的二元离散分类点。比如取到的基尼系数最小的点为at,则小于at的值为类别1,大于at的值为类别2,这样我们就做到了连续特征的离散化。要注意的是,与离散属性不同的是,如果当前节点为连续属性,则该属性后面还可以参与子节点的产生选择过程。
对于CART分类树离散值的处理问题,采用的思路是不停的二分离散特征。
2.随机森林的好处:
随机森林算法几乎不需要输入的准备。它们不需要测算就能够处理二分特征、分类特征、数值特征的数据。随机森林算法能完成隐含特征的选择,并且提供一个很好的特征重要度的选择指标。
随机森林算法训练速度快。性能优化过程刚好又提高了模型的准确性,这种精彩表现并不常有,反之亦然。这种旨在多样化子树的子设定随机特征,同时也是一种突出的性能优化!调低给定任意节点的特征划分,能让你简单的处理带有上千属性的数据集。(如果数据集有很多行的话,这种方法同样的也可以适用于行采样)
随机森林算法很难被打败。针对任何给定的数据集,尽管你常能找到一个优于它的模型(比较典型的是神经网络或者一些增益算法 boosting
algorithm),但这类算法肯定不多,而且通常建这样的模型并调试好要比随机森林算法模型要耗时的更多。这也是为何随机森林算法作为基准模型表现出色的原因。
建立一个差劲的随机森林模型真的很难!因为随机森林算法对指定使用的超参数(hyper-parameters
)并不十分敏感。为了要得到一个合适的模型,它们不需要做很多调整。只需使用大量的树,模型就不会产生很多偏差。大多数的随机森林算法的实现方法的参数设置初始值也都是合理的。
通用性。随机森林算法可以应用于很多类别的模型任务。它们可以很好的处理回归问题,也能对分类问题应付自如(甚至可以产生合适的标准概率值)。虽然我从没亲自尝试,但它们还可以用于聚类 分析问题。
下面是随机森林的实现。包括了回归和分类的算法逻辑。但在最终输出时我只输出了分类的估计值(因为我是用sklearn生成分类数据集的)
'''随机森林需要调整的参数有:
(1) 决策树的个数
(2) 特征属性的个数
(3) 递归次数(即决策树的深度)''
'import numpy as np
from numpy import *
import random from sklearn.cross_validation
import train_test_split
#生成数据集。数据集包括标签,全包含在返回值的dataset上
def get_Datasets():
from sklearn.datasets import make_classification dataSet,classLabels=make_classification(n_samples=200,n_features=100,n_classes=2)
#print(dataSet.shape,classLabels.shape)
return np.concatenate((dataSet,classLabels.reshape((-1,1))),axis=1)
#切分数据集,实现交叉验证。可以利用它来选择决策树个数。但本例没有实现其代码。
#原理如下:
#第一步,将训练集划分为大小相同的K份;
#第二步,我们选择其中的K-1分训练模型,将用余下的那一份计算模型的预测值,
#这一份通常被称为交叉验证集;第三步,我们对所有考虑使用的参数建立模型#并做出预测,然后使用不同的K值重复这一过程。
#然后是关键,我们利用在不同的K下平均准确率最高所对应的决策树个数
#作为算法决策树个数
def splitDataSet(dataSet,n_folds):
fold_size=len(dataSet)/n_folds
data_split=[]
begin=0
end=fold_size
foriinrange(n_folds): data_split.append(dataSet[begin:end,:]) begin=end end+=fold_sizereturndata_split#构建n个子集defget_subsamples(dataSet,n):subDataSet=[]foriinrange(n): index=[]forkinrange(len(dataSet)): index.append(np.random.randint(len(dataSet))) subDataSet.append(dataSet[index,:])returnsubDataSet#划分数据集defbinSplitDataSet(dataSet,feature,value):mat0=dataSet[np.nonzero(dataSet[:,feature]>value)[0],:] mat1=dataSet[np.nonzero(dataSet[:,feature]len1:return0else:return1#计算基尼指数defgini(dataSet):corr=0.0foriinset(dataSet[:,-1]): corr+=(len(np.nonzero(dataSet[:,-1]==i)[0])/len(dataSet))**2return1-corr#选取任意的m个特征,在这m个特征中,选取分割时的最优特征 defselect_best_feature(dataSet,m,alpha="huigui"):f=dataSet.shape[1] index=[] bestS=inf;bestfeature=0;bestValue=0;ifalpha=="huigui": S=regErr(dataSet)else: S=gini(dataSet)foriinrange(m): index.append(np.random.randint(f))forfeatureinindex:forsplitValinset(dataSet[:,feature]): mat0,mat1=binSplitDataSet(dataSet,feature,splitVal)ifalpha=="huigui": newS=regErr(mat0)+regErr(mat1)else: newS=gini(mat0)+gini(mat1)ifbestS>newS: bestfeature=feature bestValue=splitVal bestS=newSif(S-bestS)<0.001andalpha=="huigui":#如果误差不大就退出returnNone,regLeaf(dataSet)elif(S-bestS)<0.001:#print(S,bestS)returnNone,MostNumber(dataSet)#mat0,mat1=binSplitDataSet(dataSet,feature,splitVal)returnbestfeature,bestValuedefcreateTree(dataSet,alpha="huigui",m=20,max_level=10):#实现决策树,使用20个特征,深度为10bestfeature,bestValue=select_best_feature(dataSet,m,alpha=alpha)ifbestfeature==None:returnbestValue retTree={} max_level-=1ifmax_level<0:#控制深度returnregLeaf(dataSet) retTree['bestFeature']=bestfeature retTree['bestVal']=bestValue lSet,rSet=binSplitDataSet(dataSet,bestfeature,bestValue) retTree['right']=createTree(rSet,alpha,m,max_level) retTree['left']=createTree(lSet,alpha,m,max_level)#print('retTree:',retTree)returnretTreedefRondomForest(dataSet,n,alpha="huigui"):#树的个数#dataSet=get_Datasets()Trees=[]foriinrange(n): X_train, X_test, y_train, y_test = train_test_split(dataSet[:,:-1], dataSet[:,-1], test_size=0.33, random_state=42) X_train=np.concatenate((X_train,y_train.reshape((-1,1))),axis=1) Trees.append(createTree(X_train,alpha=alpha))returnTrees#预测单个数据样本deftreeForecast(tree,data,alpha="huigui"):ifalpha=="huigui":ifnotisinstance(tree,dict):returnfloat(tree)ifdata[tree['bestFeature']]>tree['bestVal']:iftype(tree['left'])=='float':returntree['left']else:returntreeForecast(tree['left'],data,alpha)else:iftype(tree['right'])=='float':returntree['right']else:returntreeForecast(tree['right'],data,alpha)else:ifnotisinstance(tree,dict):returnint(tree)ifdata[tree['bestFeature']]>tree['bestVal']:iftype(tree['left'])=='int':returntree['left']else:returntreeForecast(tree['left'],data,alpha)else:iftype(tree['right'])=='int':returntree['right']else:returntreeForecast(tree['right'],data,alpha)#单棵树预测测试集 defcreateForeCast(tree,dataSet,alpha="huigui"):m=len(dataSet) yhat=np.mat(zeros((m,1)))foriinrange(m): yhat[i,0]=treeForecast(tree,dataSet[i,:],alpha)returnyhat#随机森林预测defpredictTree(Trees,dataSet,alpha="huigui"):m=len(dataSet) yhat=np.mat(zeros((m,1)))fortreeinTrees: yhat+=createForeCast(tree,dataSet,alpha)ifalpha=="huigui": yhat/=len(Trees)else:foriinrange(len(yhat)):ifyhat[i,0]>len(Trees)/2: yhat[i,0]=1else: yhat[i,0]=0returnyhatif__name__ =='__main__': dataSet=get_Datasets()#得到数据集和标签print(dataSet[:,-1].T)#打印标签,与后面预测值对比RomdomTrees=RondomForest(dataSet,4,alpha="fenlei")#4棵树,分类。print("---------------------RomdomTrees------------------------")#print(RomdomTrees[0])yhat=predictTree(RomdomTrees,dataSet,alpha="fenlei") print(yhat.T)#get_Datasets()