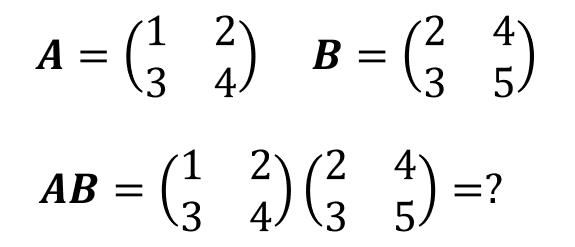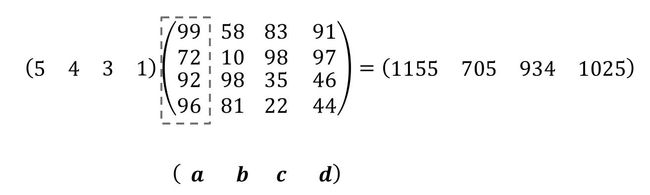本文直指线性代数最最核心的算法——矩阵乘法。
记忆矩阵乘法的最速方法
矩阵乘法,在书本上有它的公式,但是太不直观了,不好记忆,一时记住了也很快忘记。
最快的/最难以忘怀的记忆方法来了,直接上例子:
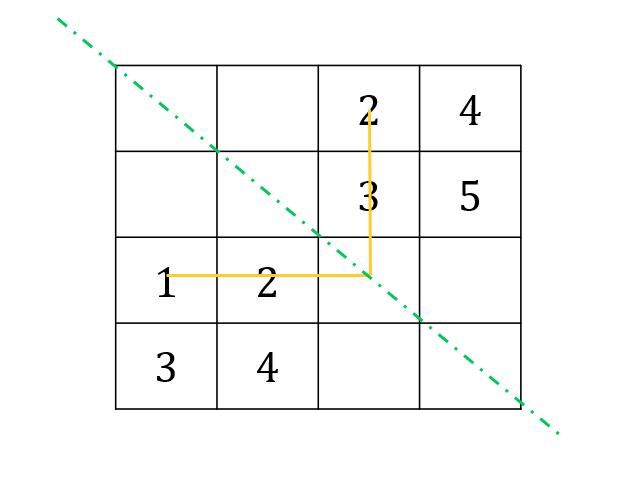
如何计算呢?采用如下方法,先起个名儿吧,叫——“占位法”。
先把后面的矩阵B向上写出一个“身位”,只要站对位置,后面就手到擒来。
然后,黄线上的数字对应相乘再相加,竖线上的位置对应相乘再相加,搞定!
再直观一点,画成表格——
占位法——用表格画更直观
怎么样,是不是看过一眼再也忘不掉?
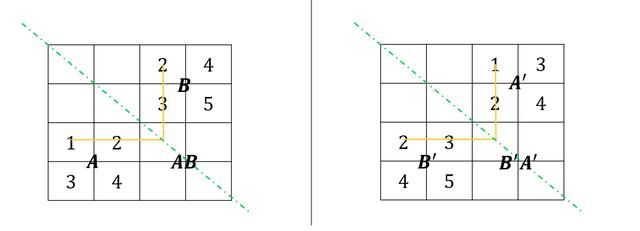
占位法解释为什么矩阵乘法没有交换率
矩阵乘法没有交换率,但是为什么?
再看一眼“占位”就知道了——
如果交换占位了,结果一样么?不一样啊,所以没有交换率。
占位法解释矩阵乘法转置换向公式
矩阵乘法虽然没有交换率,但是我们有:矩阵乘法转置换向公式:
有了占位法,这一切都顺理成章了:
这张图已经不用解释,是不是一目了然啊?公式所表达的,翻译过来,无非是:
占位法表格沿绿色虚线整体镜像,计算结果位置当然也发生了镜像!
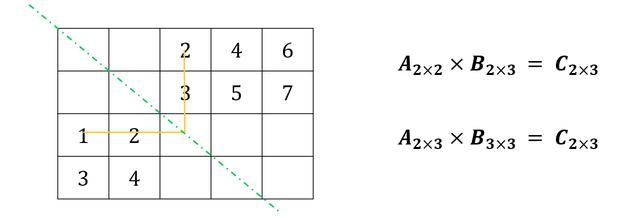
占位法解释矩阵乘法前提条件
不是什么样的两个矩阵都能相乘的,前提条件是:
A矩阵的列数 = B矩阵的行数
这怎么记啊?
其实,从占位法来看,这是再明显不过的事情了!
所谓矩阵能否相乘的条件,就是表格画不画得出来的条件啊!
想象一下,如果不满足 “A矩阵的列数 = B矩阵的行数”这个条件,就根本无法实现表格中所谓的“对应位置相乘”,因为对应的位置不够啊。
还有一个简单快捷的判断方法,把角标写出来,最相邻的角标数字相等,就可以相乘。
矩阵乘法的基础意义
上一节课,我们人为规定了列向量与行向量的不同意义,因为这样会大大帮忙我们对于向量的理解,下面我们进一步引申——
矩阵的行和列也是不同意义的,矩阵的行数 就认为是“矩阵的维数”。
为啥?
因为矩阵中的元素,是列向量(上节课),而列向量的维度就是矩阵的行数。
OK,那么矩阵乘法有什么最基础的意义?
比如:
对于B来说,原来是三维阵,经过方法A后变成了二维阵,所以2×3意义是,将三维阵降维为二维阵。
所以,单从形式上来看,矩阵相乘完成了 “维度的传递”。
乘法的本质
想要了解矩阵乘法的本质,那么您了解普通乘法的本质么?
先来一个小学乘法:
2个人,每人3个苹果,一共几个苹果?
2×3=6
上面乘法的意义是:
(2倍)×(3个苹果)=(6个苹果)
所以乘法是:
数×量
即:(方法)×(对象)=(新的对象)
“当我们暂时剥夺数量乘法的交换率,反而可以更好地理解,什么是乘法。
乘法就是把‘对象’施加‘方法’成为新的‘对象’的过程,表示为:
‘方法’ × ‘对象’
咱们把上节课的例子拿出来再仔细理解一下:
OK,如果咱们的“对象”很多,比如4位将军的信息都要分析呢,这样:
清晰吧!其实,4x4的大矩阵,也还是由4个列向量组成的:
所以——
“矩阵是向量的向量。”
好了,我们再进一步,如果要分析多位将军的多种能力,怎么办:
就这么简单!总结一句话:
乘法就是把‘对象’施加‘方法’成为新的‘对象’的过程,表示为:
‘方法’ × ‘对象’
这就是矩阵乘法的本质。
学过编程的同学可能对这两个词很熟悉,会理解得比较快。紧接着后面两节课,我们会继续切入这个本质意义,分别从“运动”和“维度”两个角度,解释方法与对象的理念。
数学与编程是完美相通的学问