- Swift 算法实战一(集合,字典,链表,栈,队列等算法)
- Swift 算法实战二(二叉树、二分搜索)
前言
这是继Swift 算法实战一(集合,字典,链表,栈,队列等算法)之后的又一篇文章,算是所学知识总结,也算是之后找工作的敲门砖。笔者这月月底要离职,即使目前这家公司给我加薪的条件,也不再想继续留下了。
这篇文章主要涉及到二叉树、二分搜索等相关,具体请看文章内容。
一、二叉树
不得不承认实际开发中很少用到二叉树相关的知识,但是面试过程中却被问道的不少。
1.1 二叉树的认识
1.1.1 概念
二叉树是 n (n >= 0)个结构的有限集合,改集合或者为空集(称为空二叉树),或者有一个根节点和两棵互不相交的、分别称为根节点的左子树和右子树的二叉树组成。
public class ZWTreeNode {
public var val: Int
public var left: ZWTreeNode?
public var right: ZWTreeNode?
public init(val: Int) {
self.val = val
}
}
1.1.2 性质
- 在二叉树的第 i 层上有至多 2^( i-1) 个结点 (i >= 1).
- 深度为 k 的二叉树至多有 2^k - 1 个节点(k >= 1).
- 具有n个结点的完全二叉树的深度为 [log (2) n] + 1 ([x] 表示不大于x的最大整数) .
1.2 判断是否为二叉查找树
二叉查找树的特点是:左子树节点值都小于根节点的值,而右子树节点值大于根节点值。那么问题就来了,给你一个二叉树,怎么通过最简单的方式,判断是否是二叉查找树。
对于解答上面这个问题,我们至少需要考虑到这两种情况。首先,二叉树但从定义上就能看出和递归有一定的关系,所以通常解决二叉树的问题,第一反应就是要和递归绑定在一起;其次,二叉树节点有为空的情况,所以一般针对空二叉树这种边界条件要做一些额外处理;
具体判断实现如下代码,代码中包含详细注释,以及调用实例展示。
//根据根节点做判断
func isValidTree(root:ZWTreeNode?) -> Bool{
return self.helper(node: root, min: nil, max: nil)
}
func helper(node:ZWTreeNode?,min:Int?,max:Int?) -> Bool {
//对于空节点的处理
guard let node = node else { return true }
//右子树要求大于根节点
if let min = min ,node.val <= min {
return false
}
//左节点要小于根节点
if let max = max,node.val >= max {
return false
}
//根据左右节点同时做判断
return helper(node:node.left,min:min,max:node.val) && helper(node:node.right,min:node.val,max:max)
}
//方法调用
let leftNode = ZWTreeNode(val: 1)
let rightNode = ZWTreeNode(val: 3)
let root = ZWTreeNode(val: 2)
root.left = leftNode
root.right = rightNode
print(isValidTree(root: root))//结果为:true
1.3 二叉树的深度
计算二叉树的深度,同样是只要知道根节点即可,同样也要借助递归实现。
//实现
func treeDepth(root:ZWTreeNode?) -> Int {
guard let root = root else {
return 0
}
return max(treeDepth(root:root.left), treeDepth(root: root.right)) + 1
}
//调用形式
let leftNode = ZWTreeNode(val: 1)
let rightNode = ZWTreeNode(val: 3)
let root = ZWTreeNode(val: 2)
root.left = leftNode
root.right = rightNode
print(treeDepth(root: root))//结果为:2
1.4 二叉树的遍历
1.4.1 三种遍历方式
二叉树的遍历多种多样,,三种常用的遍历: 前序遍历、中序遍历、后续遍历(主要依据根节点遍历的先后顺序而定义的)。
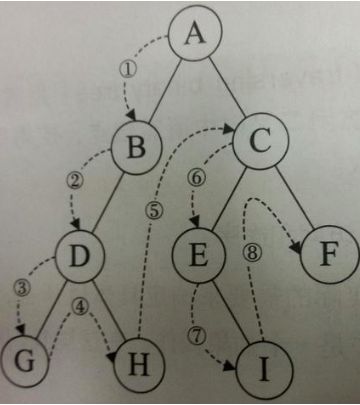
前序遍历首先访问根结点,然后前序遍历左子树,再前序遍历右子树。
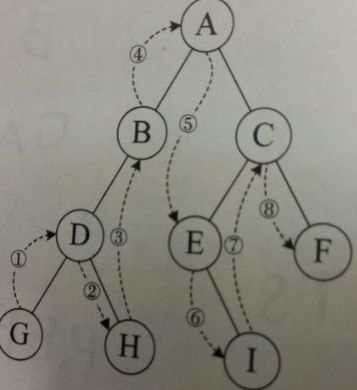
中序遍历首先遍历左子树,然后访问根结点,最后遍历右子树。在遍历左、右子树时,仍然先遍历左子树,再访问根结点,最后遍历右子树。
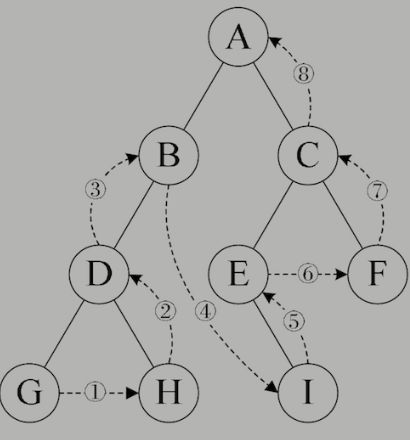
后序遍历首先遍历左子树,然后遍历右子树,最后访问根结点。在遍历左、右子树时,仍然先遍历左子树,然后遍历右子树,最后遍历根结点。
1.4.2 前序遍历实现
这里主要看一下如何借助栈来实现前序遍历。实际上其他几种遍历方式笔者是没有怎么看的。
代码逻辑的思路就是先遍历节点的左子节点,当左子节点为空的时候,就进行pop操作,获取父节点,根据父节点获取右子节点。
func formerSequenceTraversal(root:ZWTreeNode?) -> [Int] {
var arr = [Int]()
var stack = [ZWTreeNode]()
var node = root
//代码逻辑的思路就是先遍历节点的左子节点,当左子节点为空的时候,就进行pop操作,获取父节点,根据父节点获取右子节点。
while stack.isEmpty == false || node != nil{
if node != nil {
arr.append(node!.val)
stack.append(node!)//push操作,进入子节点
node = node?.left
}else{
node = stack.removeLast().right//pop操作,返回上一节点
}
}
return arr
}
前序遍历调用形式。
let subLeftLeftNode = ZWTreeNode(val: 4)
let subLeftRightNode = ZWTreeNode(val: 5)
let leftNode = ZWTreeNode(val: 1)
leftNode.left = subLeftLeftNode
leftNode.right = subLeftRightNode
let rightNode = ZWTreeNode(val: 3)
let root = ZWTreeNode(val: 2)
root.left = leftNode
root.right = rightNode
print(formerSequenceTraversal(root: root))//打印结果为:[2, 1, 4, 5, 3]
二、二分搜索
2.1 概念
一个有序数组中,如果查找某个特定的元素。可以先从中间的元素开始寻找,如果中间元素是要找的元素,直接返回;如果中间元素小于目标元素,则目标原始在大于中间元素的那一边;如果中间元素大于目标元素,则目标元素在小于中间元素的那一边。按照上面的三种情况无限的循环下去,最终就能找到目标元素。算法的时间复杂度为O(logn)。
2.2 简单实现
接下来看看如果在一个 Int 型有升序数组中,检测是否存在给定的目标值。代码如下。
//实现代码
func binarySearch(arr: [Int], target: Int) -> Bool {
var left = 0
var mid = 0
var right = arr.count - 1
while left <= right {
mid = (right - left) / 2 + left
if arr[mid] == target {
return true
} else if arr[mid] < target {
left = mid + 1
} else {
right = mid - 1
}
}
return false
}
//调用形式
let arr = [1,2,3,4,5,6,7,8]
print(binarySearch(arr: arr, target: 2))//打印结果为:true
总的来说代码实现起来比较简单,但是要注意到一点绝对不写写成mid = (right + left) / 2,否则可能发生崩溃,因为当搜索结果在右边范围的时候可能出现越界的情况,最正确的写法应当是mid = (right - left) / 2 + left。如果想获取到目标元素的下表也很简单,只要简单改写一下即可。如下代码,其中如果返回值为 -1 ,则表示不存在目标元素。
func binarySearch(arr: [Int], target: Int) -> Int {
var left = 0
var mid = 0
var right = arr.count - 1
while left <= right {
mid = (right - left) / 2 + left
if arr[mid] == target {
return mid
} else if arr[mid] < target {
left = mid + 1
} else {
right = mid - 1
}
}
return -1
}