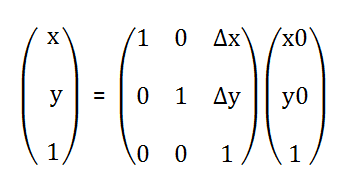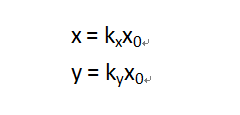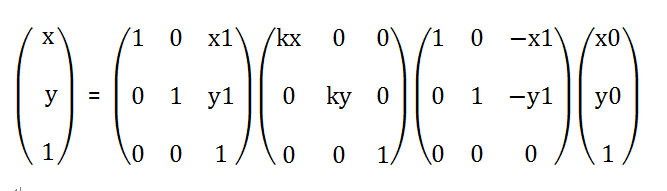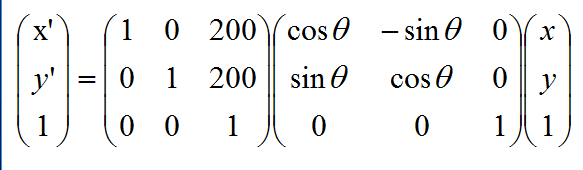Matrix 是什么
Matrix 拥有一个 3 * 3 矩阵,这个矩阵用于坐标变换。这个矩阵定义如下
Matrix 有个方法 isAffine(),判断矩阵是否为仿射矩阵。那么是什么仿射矩阵呢?下面一段话来自百度百科
仿射变换:它是一种二维坐标到二维坐标之间的线性变换,保持二维图形的“平直性”(变换后,直线还是直线,圆弧还是圆弧)、“平行性”(保持二维图形间的相对位置不变,平等线还是平等线,但是向量夹角可以发生变化)。仿射变换可以通过一系列的原子变换的复合来实现,包括平移(Translate)、缩放(Scale)、翻转(Flip),旋转(Rotation)和错切(Skew)。此类变换可以用一个 3*3的矩阵来表示,其最后一行为(0,0,1)。
Matrix 操作的仿射变换操作有平移(Translate),缩放(Scale),旋转(Rotate),错切(Skew),所以这些操作对应的矩阵最后 一行永远是(0,0,1)。
当然 Matrix 并不只是操作仿射变换,它还可以操作透视变换(Perspective),也就是矩阵最后一行操作的就是透视变换 。所以仿射变换其实就是透视变换的一种特殊情况。Matrix.setPolyToPoly() 提供了透视变换的操作,但是毕竟不是专业处理图像的,所以只能带大家入个门吧。
下面先从数学角度推导下 Matrix 操作的四种彷射变换对应的矩阵是什么。
平移的矩阵
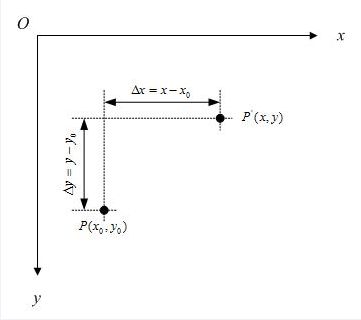
一个点 P 平移到 P' ,在坐标系表示如下
用数学公式表示
转换为坐标系表示
中间的3 * 3 矩阵就是平移对应的 Matix , ∆x 就是 x 轴的增量,∆y 就是 y 轴的增量。
旋转矩阵
旋转是有中心点的,如果把 Matrix 应用到图片,默认旋转点是图片的左上角,也就是图片的坐标原点(0,0)。
绕坐标原点旋转矩阵
用数学公式表示
用矩阵表示
中间的 3 * 3 矩阵就是绕坐标原点旋转的 Matrix。
绕非坐标原点旋转矩阵
如果图片并非绕它的坐标原点(左上角)旋转,而是绕任意点旋转,例如 图片中心点 (x1, y1),那么这个又如何计算呢?
这里我们先用数学思维思考,我们可以把(x1,y1) 作为坐标原点,那么 P 的表示应该为 (x0-x1, y0-y1),P' 的坐标为 (x-x1, y-y1),那么我们再应用旋转点是坐标原点的矩阵公式,就应该这样写
再简化下
是不是现在感觉比较明朗,等式右边第一个和第三个矩阵就是平移矩阵,我们在后面会看到如何生成这三个矩阵的结果。
我们再来理解下这个矩阵,最后两个矩阵相乘代表坐标原点移动到(x1,y1),最后三个矩阵代表以(x1, y1)为原点旋转,最后四个矩阵代表坐标原点从(x1, y1)移动到(0,0),这样是不是好记一些。
缩放矩阵
图片都是由像素点构成的,如果一个图片放大 k 倍,可以看作每个点的 x 和 y 坐标值放大 k 倍。当然缩放也有中心点的。图片默认的缩放中心为图片的左上角,也就是图片的原点(0,0)。
原点为中心的缩放
用数学表示如下
用矩阵表示如下
中间的矩阵就是绕原点绽放的 Matrix
非原点的缩放
这与非原点的旋转的数学思维是一样的,这里直接给出矩阵
中间的三个矩阵相乘就是非原点缩放 Matrix
错切矩阵
错切分为 x 轴和 y 轴的错切。
x 轴错切矩阵
x 轴错切,是保持坐标的 y 轴值不变,x 轴值的做线性变换 ,表示如下
斜率为 1/k
矩阵表示如下
矩阵表示用到的是 k,而不是斜率 1 / k,因此 k 越大,图形错切的越大。
y 轴错切矩阵
y轴错切,就是 x 轴的值不变,y 轴的值做线性变换,矩阵就不用我再推理吧,表示如下
x 轴 y 轴的错切矩阵
综合 x 轴 和 y 轴错切,统一表示如下
kx 表示 x 轴的错切值,ky 表示 y 轴的错切值。kx,ky 越大,图形错切的越大。
看完了可恶的数学公式,我们就懂得了原理 ,现在用 Matrix 的 API 来测试测试吧。
每种变换都有 setXx() ,postXx(),preXx() 方法来设置相应的变换 。如 Translate,有 Matrix.setTranslate(),Matirx.postTranslate(),Matrix.preTranslate()。我将会在代码中解释这些到底怎么用,请大家多注意,因为大部分人会用错。
默认显示一个 launcher 图标
我们先显示一个不做 Matrix 处理的图标
/**
* Created by David Chow on 2016/12/6.
*/
public class MatrixView extends View {
private Matrix mMatrix;
private Bitmap mBitmap;
public MatrixView(Context context) {
this(context, null);
}
public MatrixView(Context context, AttributeSet attrs) {
super(context, attrs);
init();
}
private void init() {
mBitmap = BitmapFactory.decodeResource(getResources(), R.mipmap.ic_launcher);
mMatrix = new Matrix();
Log.d("david", mMatrix.toString());
}
@Override
protected void onDraw(Canvas canvas) {
canvas.drawBitmap(mBitmap, mMatrix, null);
}
}
我们看看这个初始的 Matrix 矩阵是什么
Matrix{[1.0, 0.0, 0.0][0.0, 1.0, 0.0][0.0, 0.0, 1.0]}
这就是一个 3 * 3 单位矩阵 ,因此它不论前乘还是后乘都无所谓。
平移
@Override
protected void onDraw(Canvas canvas) {
mMatrix.setTranslate(200, 200); // 单位 pixel
canvas.drawBitmap(mBitmap, mMatrix, null);
Log.d("david", "translate matrix : " + mMatrix.toString());
}
我们看到了图像平移了,这个时候,我们打印 Log,可以看到矩阵的值为
translate matrix : Matrix{[1.0, 0.0, 200.0][0.0, 1.0, 200.0][0.0, 0.0, 1.0]}
我们可以看到 Matrix.setTranslate() 把单位矩阵重置为 平移的矩阵(上面数学分析得出的平移矩阵)
那么用理论的的矩阵这样表示
这样与我们上面理论是不是就一致了,这个时候我们心情是不是稍微好点了,因为我们理论终于在实际中得到验证了。后面我们将不再去这个用矩阵来验证理论,我们只打印相应的 Log 即可。
缩放
@Override
protected void onDraw(Canvas canvas) {
mMatrix.setTranslate(200, 200); // 单位 pixel
mMatrix.setScale(3, 3);
canvas.drawBitmap(mBitmap, mMatrix, null);
Log.d("david", mMatrix.toString());
}
Log打印如下
Matrix{[3.0, 0.0, 0.0][0.0, 3.0, 0.0][0.0, 0.0, 1.0]}
就算我们先用了一个无关的 Matrix.setTranslate() , 后面的 Matrix.setScale() 还是会重置矩阵为缩放的矩阵。这点大家要记住,免得以后没有达到效果,却不知道问题在哪里了。
默认的缩放中心是图片的左上角,也就是(0,0),当然我们也可以调整缩放中心位置
@Override
protected void onDraw(Canvas canvas) {
mMatrix.setScale(3, 3,mBitmap.getWidth()/2,mBitmap.getHeight()/2);
canvas.drawBitmap(mBitmap, mMatrix, null);
Log.d("david", mMatrix.toString());
}
现在缩放中心的位置为 Bitmap 的中心位置,现在看下效果
从效果看,确实是根据中心点缩放,以致图片的左上角超出了屏幕显示。
我们打印Log看下
Matrix{[3.0, 0.0, -126.0][0.0, 3.0, -126.0][0.0, 0.0, 1.0]}
那么与我们上面理论分析是不是相符,就留给大家去验证了。
Matrix.setRotate()旋转
旋转也是有中心点的,先看看个绕图片中心旋转的情况
@Override
protected void onDraw(Canvas canvas) {
mMatrix.setRotate(45, mBitmap.getWidth() / 2, mBitmap.getHeight() / 2);
canvas.drawBitmap(mBitmap, mMatrix, null);
}
Log打印如下
Matrix{[0.70710677, -0.70710677, 63.0][0.70710677, 0.70710677, -26.095451][0.0, 0.0, 1.0]}
验证理论还是交给大家了~~
Matrix.setSinCos() 也是设置旋转的,只是它不是设置角度,而是设置角度的 sin 和 cos 值。
当然默认的旋转中心也是图片的左上角
@Override
protected void onDraw(Canvas canvas) {
mMatrix.setTranslate(200, 200); // 单位 pixel
mMatrix.setScale(3, 3);
mMatrix.setRotate(30);
canvas.drawBitmap(mBitmap, mMatrix, null);
Log.d("david", mMatrix.toString());
}
同样,setRotate() 覆盖了前面的 setScale(), setTranslate()
打印下矩阵信息
Matrix{[0.8660254, -0.5, 0.0][0.5, 0.8660254, 0.0][0.0, 0.0, 1.0]}
根据我们上面讲的,这个里面的小数值 ,对应角度为 30 的 sin 或者 cos 值,大家可以自己用计算器算算~~
现在看下效果图
我们发现这个移出了屏幕了,因此现在我们来平移下
@Override
protected void onDraw(Canvas canvas) {
mMatrix.setTranslate(200, 200); // 单位 pixel
mMatrix.setScale(3, 3);
mMatrix.setRotate(30);
mMatrix.preTranslate(200, 200);
canvas.drawBitmap(mBitmap, mMatrix, null);
Log.d("david", mMatrix.toString());
}
一个奇怪的现象就产生了,X 方向的平移呢?其实这是因为矩阵乘法不满足交换律的原因。mMatrix.preTranslate() 意思是用 mMatrix 矩阵前乘 translate 矩阵,数据表示如下
这个结果就不用我算了吧,很显然实际偏移的并不是200,200。那么我们如何让它既旋转30°,又正常偏移200,200呢。 我们可以让 mMatrix 后乘 translate
@Override
protected void onDraw(Canvas canvas) {
canvas.drawLine(0, 0, 200, 200, mPaint);
mMatrix.setRotate(30);
mMatrix.postTranslate(200, 200);
canvas.drawBitmap(mBitmap, mMatrix, null);
}
为了看到我们确实是偏移了200,200,我画了一条红色的线
那么我们用数学来表达下
大家计算下,是不是既旋转了又平移了200,200?
我用这个例子是为了让大家理解 preXx() 和 postXx() 的区别,希望大家自己动手试试加深理解。
再给大家一个 Tip,如果想要平移达到效果,最后调用 postTranslate()。
Matrix.setSkew() 错切
先用默认中心点,即图片的左上角进行错切。为了看到效果,我们先平移200,200,再进行错切变换
mMatrix.setTranslate(200, 200);
mMatrix.preSkew(1, 0);
canvas.drawBitmap(mBitmap, mMatrix, null);
这里我并没有遵循上面的例子最后用 postTranslate(),这是因为根据矩阵的特性,这样刚好不影响平移,我们可以打印Log看看矩阵
Matrix{[1.0, 1.0, 200.0][0.0, 1.0, 200.0][0.0, 0.0, 1.0]}
我没说错吧,但是如果你再操作下,就有问题了,例如例如 postScale(3,3),就会平移 600,600了。当然如果你最后还是调用 postTranslate(200,200) ,会正常平移400,400。
大家别看我说的很简单,自动写的时候就会遇到各种问题,因此大家在看的时候还是多动手。
再看看中心点不是原点的错切,例如用图片的左下角来错切。
@Override
protected void onDraw(Canvas canvas) {
mMatrix.setTranslate(200, 200);
mMatrix.preSkew(1, 0, 0, mBitmap.getHeight());
canvas.drawBitmap(mBitmap, mMatrix, null);
Log.d("david", mMatrix.toString());
}
打印Log
Matrix{[1.0, 1.0, 74.0][0.0, 1.0, 200.0][0.0, 0.0, 1.0]}
理论验证继续留给大家了~~
思考
我们使用 Matrix API 的时候,我们只是一名 Developer,但是我们要把自己当做一个 Designer,我们思考下,其实我们可以利用矩阵做很多想要的效果,因为我们可以用 Matrix.setValues() 来设置自己想要的矩阵 ,因此我们可以设计对称效果,倒影效果等等,这就要大家去发掘啦~~
结束
这篇文章大家入门 Matrix,当然这是为了我后面文章打基础的,还是那句话,多动手,如果遇到问题解决不了,欢迎大家留言讨论。 如果大家觉得还不错,可以点个赞,甚至来一波关注不惜留恋_, what's a nice day~~
参考文章
http://blog.csdn.net/cquwentao/article/details/51445269
http://baike.baidu.com/link?url=D4AHXGFs4yjlXg74jY1xU5shk1z--hyAe28ynSWaadyI0IrVQSYh6ueJpgpHbJwk8mGdrWEscclauzzMo81vv6qb__77JQdpSmgcgF6S1HnYJDHDdEGRquy3sCYf7UPa
http://baike.baidu.com/link?url=sqH8yi74VwnyBq3Uhr_tn6pCF9lHNZWmRF0j_4hc3gLy45vPBFM9eGnN3BrpUou8jiPaXtDxg_B7WvNGEXep8UuQr7q8tHk8DTWv34FcKKK-1iQy5W7-2IBPGxsab5Wr