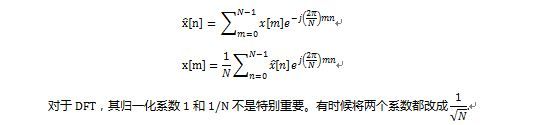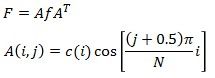1.转自:离散余弦变换(DCT)的定义_小火车_新浪博客
已知离散傅里叶变换(DFT)为:
由于许多要处理的信号都是实信号,在使用DFT时由于傅里叶变换时由于实信号傅立叶变换的共轭对称性导致DFT后在频域中有一半的数据冗余。
离散余弦变换(DCT)是对实信号定义的一种变换,变换后在频域中得到的也是一个实信号,相比DFT而言,DCT可以减少一半以上的计算。DCT还有一个很重要的性质(能量集中特性):大多书自然信号(声音、图像)的能量都集中在离散余弦变换后的低频部分,因而DCT在(声音、图像)数据压缩中得到了广泛的使用。由于DCT是从DFT推导出来的另一种变换,因此许多DFT的属性在DCT中仍然是保留下来的。
推导N点长实序列的DCT,首先来定义一个新的长度为2N的序列:
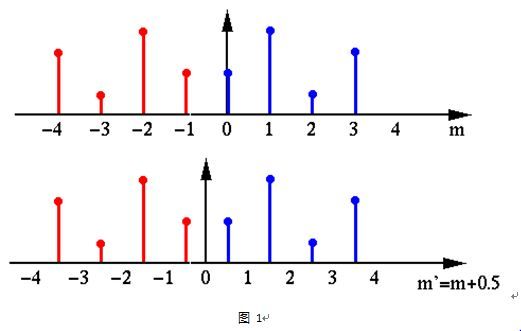
可看作是将周期为N的序列x[m]做一个周期延拓成一个周期为2N的序列。如图1中第一张图。
再来看图1中第一张图是关于x = -1/2对称的,要让他关于x = 0对称需要将其向右平移1/2个单位,得到x’[m] = x’[m – 1/2]就是关于x = 0对称的周期序列了(如图1中第二张图)。
然后求这个2N序列的DFT:
就是DCT-2型离散余弦变换.从上面的过程也可以直接看出,离散余弦变换相当于一个长度大概是它两倍的离散傅里叶变换.
变换后的x[n]是以2N为周期,偶对称的序列: X[N+n] = X[N+n-2N] = X[n-N] = x[N-n]
定义变换矩阵C[n,m]:
用计算机计算DCT-2 (用的是O(n^2)朴素算法,用于验证正交特性以及观察其频域数据):
DCT的结果:
对相同序列FFT的结果:
比较DFT和FFT的结果可以观察出DCT变换只有实部,而DFT变换后有虚部。在这个例子中DCT在频域中只用3个点就可以表示这个信号,而DFT变换后在频域中需要5个点来表示信号。
参考:http://fourier.eng.hmc.edu/e161/lectures/dct/node1.html
2.转自:二维DCT变换 - Wuyuan's Blog
写这篇文章的目的主要是为了给x264打好基础,x264用的是整数DCT变换,所以就先来说说DCT变换吧。
DCT(Discrete Cosine Transform),又叫离散余弦变换,它的第二种类型,经常用于信号和图像数据的压缩。经过DCT变换后的数据能量非常集中,一般只有左上角的数值是非零的,也就是能量都集中在离散余弦变换后的直流和低频部分,下面我会用matlab来演示整个过程。
1.一维DCT变换
我们首先来看看一维的DCT变换,这是二维的基础。一维的DCT变换共有8种,其中最实用的是第二种形式,公式如下:
其中c(u)是加上去一个系数,为了能使DCT变换矩阵成为正交矩阵,在后面二维变换将看到他的作用。N是f(x)的总数。相比其他几种形式,他的运算还是比较简单的,因此也用的比较广。
2.二维DCT变换
二维DCT变换是在一维的基础上再进行一次DCT变换,这个比较好理解,直接看公式:
这里我只讨论两个N相等的情况,也就是数据是方阵的形式,在实际应用中对不是方阵的数据都是先补齐再进行变换的。为了matlab仿真方便点,写成矩阵形式:
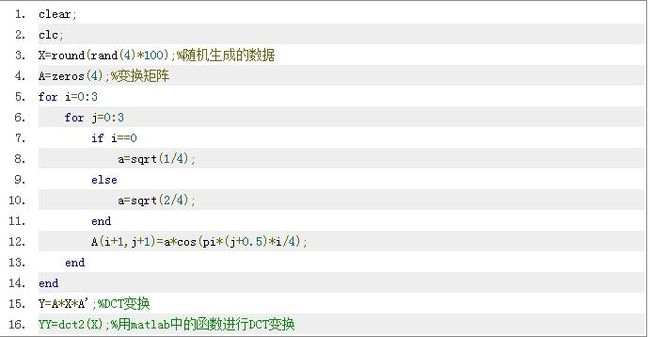
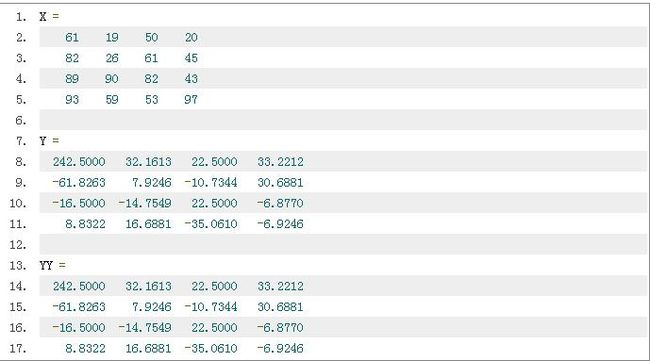
下面就用matlab来模拟一下,使用随机生成的4x4矩阵作为输入,程序如下:
Y是使用上面的公式进行变换,YY是用matlab自带的dct2函数变换,结果是是:
可以看出Y和YY的结果是一样的,这也进一步验证了上面的公式是正确的。由于X是我随机生成的,相关性很小,变换后的结果比较乱;如果是信号或图像这样相关性比较大的数据的话,数值会集中在左上角,右下角一般都是零,再使用“之”字型扫描得到数据流会包含很多连续的零,编码后数据量会非常小,这就是DCT变换带来的好处。
3.二维DCT反变换
DCT逆变换的公式如下:
矩阵形式可以由正变换的公式直接推出来,因为在A中加了c(i)这个系数,使得A成为了正交矩阵,所以我们就可以这样做:
在用matlab来验证是否能反变换出原来的数据:
X使用的是上面正变换用的数据,运行后得到的X1为:
X1=
61.000019.000050.000020.0000
82.000026.000061.000045.0000
89.000090.000082.000043.0000
93.000059.000053.000097.0000
和X完全相等。在实际进行编码的时候,比如JPEG压缩的时候,只会对Y左上角的数据进行传输,所以解码出来的内容不会完全和原来的相同。
4.整数DCT变换
说道DCT就顺便提一下x264中的整数DCT变换,整数DCT变换是以DCT变换为基础的,为了减少计算量做的一些调整,下面我写一下整数DCT变换公式的大致推导过程:
然后根据A是正交矩阵,把c=bd带入A中,使行向量为单位向量可以得到d=0.4142。令d=0.5,得到b*b=0.4,代入上面的式子中,把0.5提取出来放到右边的点乘中就得到了:
这样在对大括号部分进行计算时就都是加法和减法了,而且在精度上没有太大降低。在x264实际编码中,变换和量化是一起进行的,使得编码速度有了很大的提高。