目录
1、相关术语
2、图的表示
2.1、邻接矩阵
2.2、邻接表
3、图的遍历
3.1、深度优先搜索
3.2、广度优先搜索
3.3、二者的比较
4、拓扑排序
5、最短路径算法
5.1、无权图中的最短路径
5.2、有权图中的最短路径
5.3、Bellman-Ford算法
6、最小生成树
6.1、Prim算法
6.2、Kruskal算法
正文
1、相关术语
- 图:一个图可以表示为 (V,E),其中 V 是结点的集合,称为 顶点 ;E是顶点对的集合,称为 边 。顶点和边代表位置和存储元素,下述是相关定义:
-
有向边:
1)有序顶点对(u,v)。
2)第一个顶点u是源点。
3)第二个顶点v是终点。
-
无向边
1)无序顶点对(u,v)。
-
有向图
1)所有的边都是有向边。
-
无向图
1)所有的边都是无向边。
- 无环图称为 树,树是不包含环的连通图。
-
自环指的是一条连接顶点及其自身的边。
- 顶点的度是指关联该顶点的边的数目。
- 子图是图的边(及边所关联的顶点)的子集形成的图。
-
图中的路径是指一系列的相邻顶点。简单路径是一条不包含重复顶点的路径。
-
环路是起点与终点相同的路径。简单环路是不包含重复顶点和边的环(除了起点和终点外)。
- 如果两个顶点之间存在一条路径,则称这两个顶点是连通的。
- 如果图中每对顶点之间都有路径相连,则该图是连通图。
-
如果一个图是非连通的,那么它由一组连通分量构成。
- 连通图的生成树是一个包含所有顶点的子图,并且是一棵单独的树。图的生成森林是连通分量的生成树的集合。
-
在一个有权图中,给每条边赋值一个整数(权重)来代表(距离或花费)。
2、图的表示
- 图有以下两种表示形式:
1)、邻接矩阵
2)、邻接表
2.1、邻接矩阵
-
图的表示需要顶点数、边数以及它们之间的连接关系。该方法采用一个大小为 V*V的矩阵Adj,其中矩阵的指为布尔值。如果存在一条从u到v的边,则设置Adj[u,v]=1,否则为0。
-
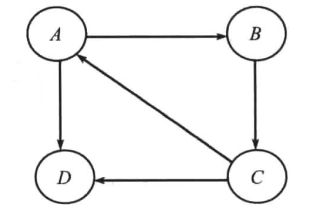
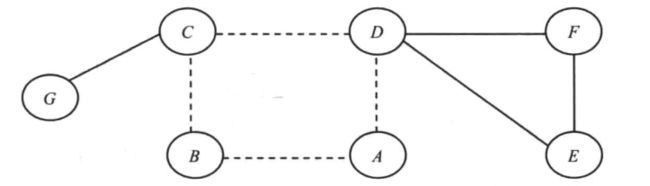
图2-1的邻接矩阵可以表示为:
- 读无向图的代码实现如下:
public class Graph {
private bool[,] adjMatrix;
private int vertexCount;
public Graph(int vertexCount) {
this.vertexCount = vertexCount;
adjMatrix = new bool[vertexCount,vertexCount];
}
public void addEdge(int i,int j) {
if (i >= 0 && i < vertexCount && j >= 0 && j < vertexCount) {
adjMatrix[i, j] = true;
adjMatrix[j, i] = true;
}
}
public void removeEdge(int i,int j) {
if (i >= 0 && i < vertexCount && j >= 0 && j < vertexCount) {
adjMatrix[i, j] = false;
adjMatrix[j, i] = false;
}
}
public bool isEdge(int i,int j) {
if (i >= 0 && i < vertexCount && j >= 0 && j < vertexCount) {
return adjMatrix[i, j];
}
else {
return false;
}
}
}
2.2、邻接表
-
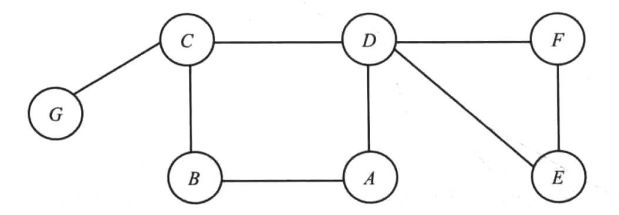
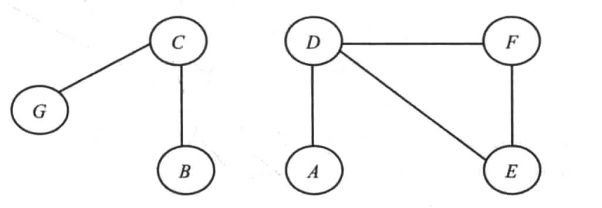
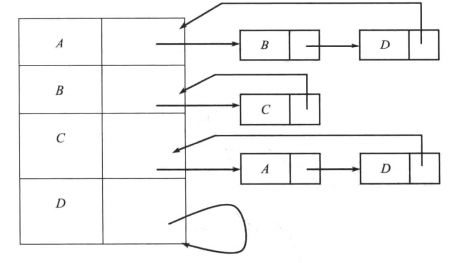
图的邻接表表示方式如图2-3所示。在这种方式下,所有与某个顶点v相连的顶点都在v的邻接表中列出,采用链表容易实现。
- 代码实现
public class GraphByLinkList {
private ArrayList vertices;
private ListNode[] edges;
private int vertexCount;
public GraphByLinkList(int vertexCount) {
this.vertexCount = vertexCount;
vertices = new ArrayList();
edges = new ListNode[vertexCount];
for(int i = 0; i < vertexCount; i++) {
vertices.add(i);
edges[i] = new ListNode();
}
}
public void addEdge(int source,int destination) {
int i = vertices.indexOf(source);
int j = vertices.indexOf(destination);
if (i != -1 || j != -1) {
edges[i].insertAtBeginning(destination);
edges[j].insertAtBeginning(source);
}
}
}
- 邻接表的缺点:以删除某个结点为例,如果直接删除该结点是可以做到的,然而,在邻接表中当该结点和其他结点有边相连时,则必须搜索其他结点对应的链表来删除该结点。
3、图的遍历
3.1、深度优先搜索
- 深度优先搜索的算法原理类似于树的前序遍历,本质上也是用栈来实现。以 “迷宫” 为例子,为了走出迷宫,这个人需要访问每条 路径 和每一个 十字路口(最坏情况下)。假设此人使用两种颜色的涂料来标记已经经过的十字路口。当发现一个十字路口时,将其标为 灰色 ,并且继续往更深处走。当到达一个 “末端” 时,则表明从标记为 灰色 的十字路口出发的所有路径都已经访问过,并且将该十字路口标记为 黑色 。
- 迷宫的十字路口是图的 顶点 ,而十字路口之间的路径就是图的 边,从末端返回的过程叫作 “回溯”。算法便是尝试从起点开始尽可能 深 地访问图中的结点,直到 回溯到先前的灰色结点。在算法中,包括如下类型的边:
1)、树边:遇到一个新顶点的边。
2)、前向边:从祖先到子孙的边。
3)、回退边:从子孙到祖先的边。
4)、交叉边:在一棵树或子树之间的边。 - 初始时所有顶点都被标记为未被访问过(false)。深度优先搜索算法从图中的一个顶点u开始,首先考虑从u到其它顶点的边。如果该边通往一个已经被访问过的顶点,则 回溯 到当前顶点u。如果该边通往一个 未曾访问过的顶点 ,则到达该顶点,并从该顶点进行访问,即 将新的顶点变为当前顶点 。重复这个过程直到算法到达 “末端”。然后从 “末端” 点开始 回溯 。当回溯到 起始点 时结束。
- 代码实现
public class Vertex {
public char label { get; set; }
public bool visited { get; set; }
public Vertex(char label) {
this.label = label;
visited = false;
}
}
public class Graph {
private const int maxVertices = 20;
///
/// 访问表
///
private Vertex[] vertexList;
///
/// 邻接表
///
private int[,] adjMatrix;
///
/// 顶点数
///
private int vertexCount;
///
/// 访问路径
///
private Stack theStack;
public Graph() {
vertexList = new Vertex[maxVertices];
adjMatrix = new int[maxVertices, maxVertices];
vertexCount = 0;
for(int y = 0; y < maxVertices; y++) {
for(int x = 0; x < maxVertices; x++) {
adjMatrix[x, y] = 0;
}
}
theStack = new Stack();
}
public void addVertex(char label) {
vertexList[vertexCount++] = new Vertex(label);
}
public void addEdge(int start,int end) {
adjMatrix[start, end] = 1;
adjMatrix[end, start] = 1;
}
public void displayVertex(int v) {
Console.Out.WriteLine(vertexList[v].label);
}
///
/// 深度优先搜索算法
///
public void dfs() {
vertexList[0].visited = true;
displayVertex(0);
theStack.Push(0);
while (theStack.Count > 0) {
int v = getAdjUnvisitedVertex(theStack.Peek());
if (v == -1) {
theStack.Pop();
}
else {
vertexList[v].visited = true;
displayVertex(v);
theStack.Push(v);
}
}
for(int j = 0; j < vertexCount; j++) {
vertexList[j].visited = false;
}
}
///
/// 获取从v顶点开始路径中,未被访问的顶点
///
/// 起始点
/// 未访问点
public int getAdjUnvisitedVertex(int v) {
for(int j = 0; j < vertexCount; j++) {
if (adjMatrix[v, j] == 1 && vertexList[j].visited == false) {
return j;
}
}
return -1;
}
}
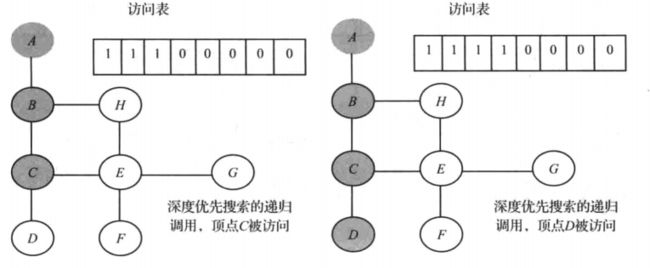
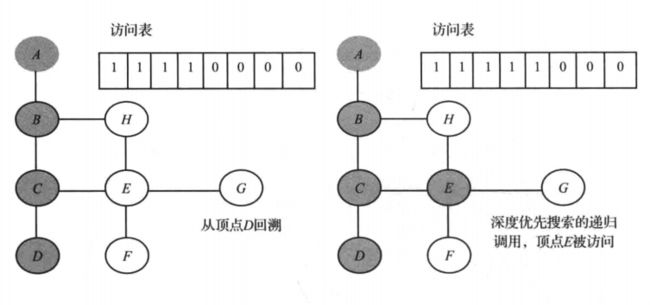
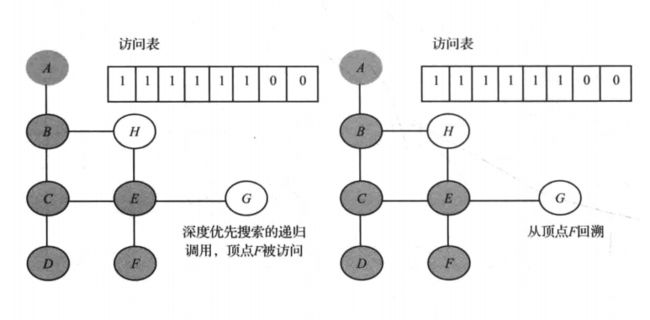
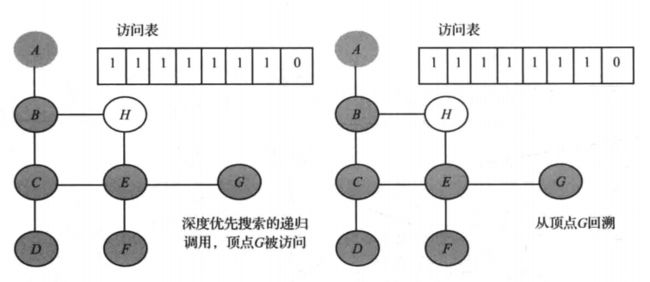
- 在下图示例中,灰色 表示该顶点被访问过,需要注意的是 访问表 何时被更新。
3.2、广度优先搜索
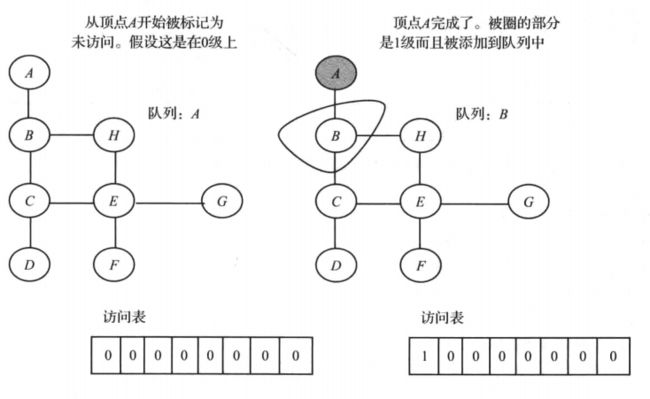
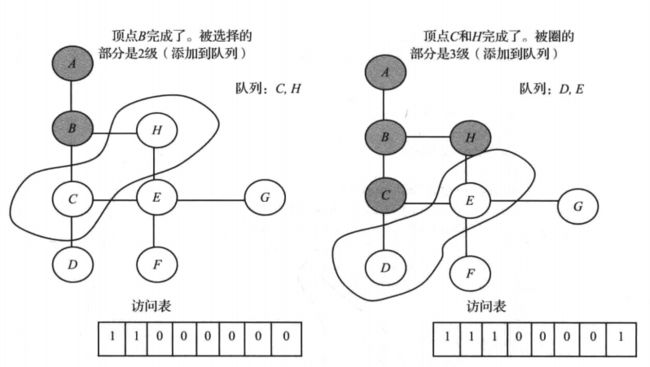
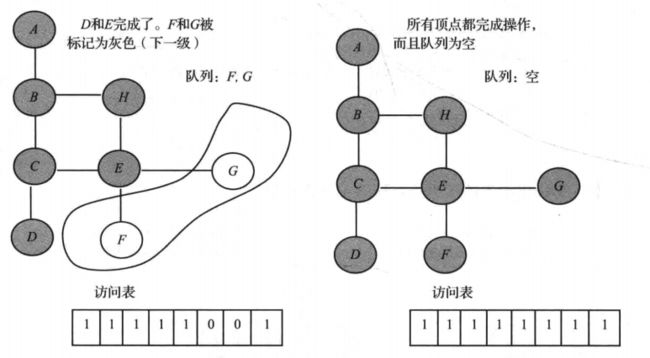
- 广度优先搜索算法的原理类似 树的层次遍历,并且算法使用了 队列。初始时,从一个给定的顶点出发,该顶点位于 第0层。第一步,它将访问所有处于 第一层 的顶点(即从图中到起始顶点距离为1的顶点)。第二步,访问 第二层 所有的顶点,即与 第一层 相邻的顶点。算法重复该过程,直至图的所有层访问一遍。
- 假设初始时所有顶点都被标记为未曾访问过(false),已经处理过并且从队列移除 的顶点标记为已访问过(true)。利用 另一个队列 来表示已经访问过的顶点的集合,该队列记录顶点第一次被访问的顺序。
- 代码实现
public class Vertex {
public char label { get; set; }
public bool visited { get; set; }
public Vertex(char label) {
this.label = label;
visited = false;
}
}
public class Graph {
private const int maxVertices = 20;
///
/// 访问表
///
private Vertex[] vertexList;
///
/// 邻接表
///
private int[,] adjMatrix;
///
/// 顶点数
///
private int vertexCount;
///
/// 访问路径
///
private Queue theQueue;
public Graph() {
vertexList = new Vertex[maxVertices];
adjMatrix = new int[maxVertices, maxVertices];
vertexCount = 0;
for(int y = 0; y < maxVertices; y++) {
for(int x = 0; x < maxVertices; x++) {
adjMatrix[x,y] = 0;
}
}
theQueue = new Queue();
}
public void addVertex(char label) {
vertexList[vertexCount++] = new Vertex(label);
}
public void addEdge(int start, int end) {
adjMatrix[start, end] = 1;
adjMatrix[end, start] = 1;
}
public void displayVertex(int v) {
Console.Out.WriteLine(vertexList[v].label);
}
///
/// 广度优先搜索算法
///
public void bfs() {
vertexList[0].visited = true;
displayVertex(0);
theQueue.Enqueue(0);
int v2;
while (theQueue.Count > 0) {
int v1 = theQueue.Dequeue();
while ((v2 = getAdjUnvisitedVertex(v1)) != -1) {
vertexList[v2].visited = true;
displayVertex(v2);
theQueue.Enqueue(v2);
}
}
for (int j = 0; j < vertexCount; j++) {
vertexList[j].visited = false;
}
}
///
/// 获取从v顶点开始路径中,未被访问的顶点
///
/// 起始点
/// 未访问点
public int getAdjUnvisitedVertex(int v) {
for (int j = 0; j < vertexCount; j++) {
if (adjMatrix[v, j] == 1 && vertexList[j].visited == false) {
return j;
}
}
return -1;
}
}
-
广度优先搜索算法的示例图如下:
3.3、二者的比较
- 深度优先搜索 的最大优势在于它的 内存开销 要远远 小于广度优先搜索 ,因为它不需要存储每一层的结点的所有孩子结点指针。但其实二者哪个更好?答案取决于需要解决的问题类型。广度优先搜索每次访问一层,若预先知道需要搜索的结果处在一个 较低的深度,那么 广度优先搜索 是合适的。如果处于 较大深度,那么 深度优先搜索 是更好的选择。
| 应用 | 深度优先搜索 | 广度优先搜索 |
|---|---|---|
| 生成森林、连通分量、路径、环路 | 是 | 是 |
| 最短路径 | 是 | |
| 内存开销最小 | 是 |
4、拓扑排序
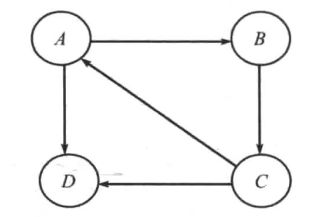
- 拓扑排序 是在一个 有向无环图 中对 顶点 的排序。在这个有向无环图中,每个顶点都排在所有以它为起点的相邻结点之前。
- 如果排好序的 所有连续顶点对之间都是有边相连,那么这些边会在图中形成一个 有向哈密顿路径。若有 一条 哈密顿路径存在,则拓扑排序的的顺序是 唯一的。如果 没有 形成哈密顿路径,则图中可能有 两个或者多个 的拓扑排序。
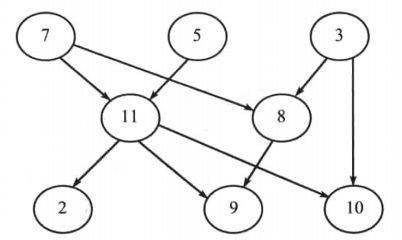
- 图4-1中,7,5,3,11,8,2,9,10 和 3,5,7,8,11,2,9,10都是 拓扑排序。
- 初始时,计算所有顶点的入度,并从 入度为0的顶点出发,因为这些顶点没有任何先决条件。可以使用队列来跟踪这些入度为0的顶点。
- 将所有 入度为0 的顶点放入队列中,当队列不为空时,从队列中移除顶点v,并将v的所有 相邻顶点的入度减1 。一旦某个顶点 入度变为0,就将其放入队列中。因此,拓扑排序就是队列中的顶点 出队的顺序。
- 代码实现
public void TopologicalSort(Graph G) {
LLQueue Q = new LLQueue();
int counter;
int v;
counter = 0;
//初始入队所有入度为0的顶点
for (v = 0; v < G.vertexCount; v++) {
if (G.indegree[v] == 0) {
Q.enQueue(v);
}
}
while (!Q.isEmpty()) {
v = Q.deQueue();
topologicalOrder[v] = ++counter;
//获取与v相邻的所有顶点
var list = GetAdjacentTo(v);
foreach(int w in list) {
if (--G.indegree[w] == 0) {
Q.enQueue(w);
}
}
}
if (counter != G.vertexCount) {
Console.Out.Write("Graph has cycle");
}
Q.deleteQueue();
}
5、最短路径算法
- 给定一个图G=(V,E)和一个特殊顶点s,需要查找从s到图中其它顶点的最短路径。但是根据输入图形的类型不同,最短路径算法会有相应的变化,主要包括以下三种:
1)无权图中的最短路径
2)有权图中的最短路径
3)带有负边的有权图中的最短路径
5.1、无权图中的最短路径
- 假设要寻找 某个输入顶点s 到所有其他顶点的 最短路径 。无权图是有权图最短路径问题的特例,即边的权重都是1。
- 算法实现的数据结构:
1)距离表:①当前顶点到源点的距离;②路径——包含最短路径上经过的顶点。
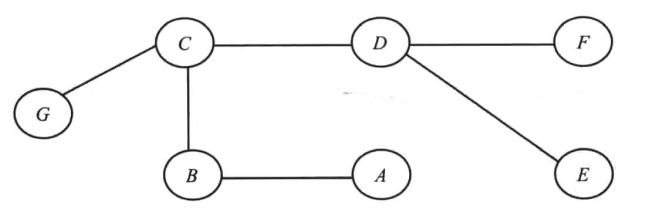
2)一个用于实现 广度优先搜索的队列,它包含到 源点距离已知的结点 以及 尚未访问的相邻顶点。 - 以图5-1为例,设s=C,从C到C的距离是 0。初始时,C到其它顶点的距离未确定,将距离表上除了C以外的其它顶点的第二列(到源点的距离)设为 -1,如下表所示。
| 顶点 | Distance[v] | 获得Distance[v]的前一个顶点 |
|---|---|---|
| A | -1 | —— |
| B | -1 | —— |
| C | 0 | —— |
| D | -1 | —— |
| E | -1 | —— |
| F | -1 | —— |
| G | -1 | —— |
- 代码实现:
public void UnWeightedShortestPath(Graph G, int s) {
LLQueue Q = new LLQueue();
int v;
Q.enQueue(s);
for (int i = 0; i < G.vertexCount; i++) {
Distance[i] = -1;
}
Distance[s] = 0;
while (!Q.isEmpty()) {
v = Q.deQueue();
//获取与顶点v相邻的顶点集合
var list = GetAdjacentTo(v);
foreach (int w in list) {
//每个顶点最多检查一次
if (Distance[w] == -1) {
Distance[w] = Distance[v] + 1;
//存放最短路径中的上一个顶点
Path[w] = v;
//每个顶点最多入队一次
Q.enQueue(w);
}
}
}
Q.deleteQueue();
}
- 如果使用 邻接表 表示 ,则运行时间为 O(| E |+| V |)。在 for循环中,算法检查每个顶点的 出边;在while循环中所有访问过的边的和等于边的数目,即为 O(| E |)。
- 如果使用 矩阵 表示,则时间复杂度是 O(| V |^2),因为必须在 长度为 | V | 的矩阵中读入一整行,以便查找给定顶点的相邻顶点。
5.2、有权图中的最短路径(Dijkstra算法)
- 算法:与 5.1的无权图的最短路径 类似,也将会使用 距离表。算法在距离表中保存从源点到顶点v的最短路径。Distance[v]记录从s到v的距离。源点到它自身的最短距离为0。而距离表中将一个顶点到另一个顶点的距离设为 -1 来表示 尚为访问过的顶点。
1)采用贪婪法:总是选取最接近源点的顶点。
2)使用优先队列并按照到s的距离来存储未被访问过的顶点。
3)不能用于权值为负值的情况。 - 举例说明:
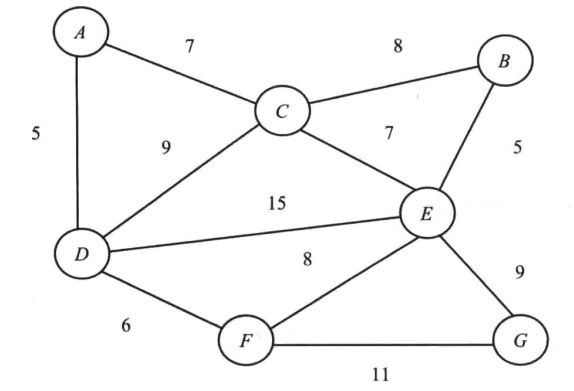
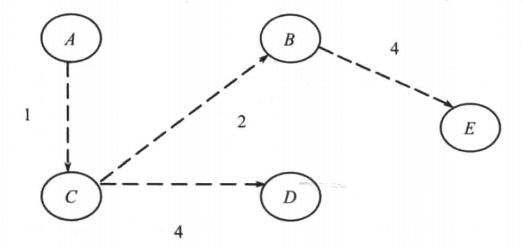
如图5-2所示的有权图中有A~E5个顶点,两个顶点之间的值即为边的权重,利用 Dijkstra算法查找从源点A到其它顶点的最短路径。
初始化距离表为:
| 顶点 | Distance[v] | 获得Distance[v]的前一个顶点 |
|---|---|---|
| A | 0 | —— |
| B | -1 | —— |
| C | -1 | —— |
| D | -1 | —— |
| E | -1 | —— |
| F | -1 | —— |
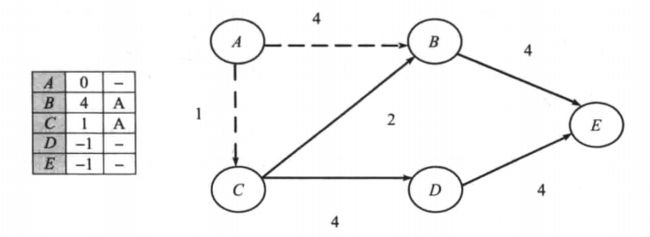
1)、完成初始化后,从顶点A能够到达B和C,因此在距离表中以相应的边权值来更新顶点B和C的可达性,如图5-3所示。
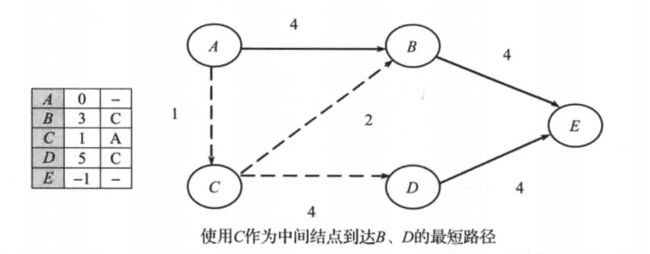
2)、从距离表中选择一个 最小距离,可知最小距离是 顶点C。这表明必须通过这两个顶点 (A和C)才能到达其它顶点。而 A和 C都能到达顶点 B,这种情况下要选择 代价小的路径,因为C到B的代价(1+2)更小,所以距离表中用3和顶点 C来更新。通过 C还可以到达顶点 D,因此也相应的更新距离表中顶点 D的值。如图5-4所示。
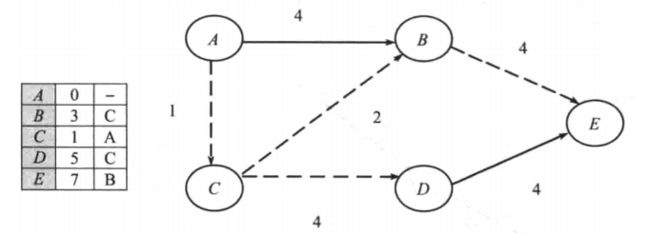
3)、当前唯一未被访问的结点为 E,为了到达 E,需要找出所有可以到达 E的路径并选择其中代价最小的路径,可以发现,当使用经过 C到达的 B顶点作为中间顶点时具有 最小代价。如图5-5所示。
4)、最终产生的最小代价树如图5-6所示。
- 代码实现:
public void Dijkstra(Graph G,int s) {
Heap PQ = new Heap();
int v;
PQ.enQueue(s);
for(int i = 0; i < G.vertexCount; i++) {
Distance[i] = -1;
}
Distance[s] = 0;
while (!PQ.isEmpty()) {
v = PQ.deleteMin();
//获取与顶点v相邻的顶点集合
var list = GetAdjacentTo(v);
foreach (int w in list) {
int d = Distance[v] + weight[v, w];
//判断顶点w是否被访问过
if (Distance[w] == -1) {
//更新顶点w到源点的值
Distance[w] = d;
//加入优先队列
PQ.enQueue(w);
//更新顶点w的最短路径的上一顶点
Path[w] = v;
}
//判断当前路径是否最短
if (Distance[w] > d) {
Distance[w] = d;
//更新顶点w的最短路径的上一顶点
Path[w] = v;
}
}
}
}
5.3、Bellman-Ford算法
- Dijkstra算法不能处理边值为负的情况。这是由于当某个顶点u被标记为已访问时,仍然存在这样一种可能,即存在一条从某个未被访问过的顶点v到u的负路径。在这种情况下,从s出发经过v再到u的路径长度小于从s出发到u但不经过v的路径的长度。
- Dijstra算法与无权图算法相结合可以解决这个问题,用S初始化队列,然后在每一步将顶点v出队,找到v的所有相邻顶点w使得:到v的距离+边(v,w)的权值<到w的原有距离。对w的原有距离和路径进行更新,并且若w不在队列中,则入队。可以为每个顶点设置一个标记位来表示它是否在队列中,重复该过程直至队列为空。
- 代码实现:
public void BellmanFordAlgorihm(Graph G,int s) {
LLQueue Q = new LLQueue();
int v;
Q.enQueue(s);
//假定用 INT_MAX填充距离表
Distance[s] = 0;
while (!Q.isEmpty()) {
v = Q.deQueue();
//获取与顶点v相邻的顶点集合
var list = GetAdjacentTo(v);
foreach (int w in list) {
int d = Distance[v] + weight[v, w];
if (Distance[w] > d) {
Distance[w] = d;
Path[w] = v;
if (!Q.isExist(w)) {
Q.enQueue(w);
}
}
}
}
}
6、最小生成树
- 图的最小生成树是一个包含所有顶点的子图并且是一棵树。一个图可能有多个生成树。有以下两个著名算法用于解决最小生成树问题:
1)、Prim算法
2)、Kruskal算法
6.1、Prim算法
- 与Dijkstra算法几乎相同,Prim算法也利用距离表来保存距离和路径。唯一的区别是,由于距离的定义不同,所以更新操作略有不同。
- 代码实现:
public void Prims(Graph G,int s) {
Heap PQ = new Heap();
int v;
PQ.enQueue(s);
//假设距离表用 -1 填充
Distance[s] = 0;
while (!PQ.isEmpty()) {
v = PQ.deleteMin();
//获取与顶点v相邻的顶点集合
var list = GetAdjacentTo(v);
foreach (int w in list) {
int d = Distance[v] + weight[v, w];
if (Distance[w] == -1) {
//更新顶点w到源点的值
Distance[w] = d;
//加入优先队列
PQ.enQueue(w);
//更新顶点w的最短路径的上一顶点
Path[w] = v;
}
//判断当前路径是否最短
if (Distance[w] > d) {
Distance[w] = weight[v,w];
//更新顶点w的最短路径的上一顶点
Path[w] = v;
}
}
}
}
6.2、Kruskal算法
- 算法:从 V 个不同的树开始,其中 V 为图中的顶点。当构造最小生成树时,算法每次选择一条权值最小且不会形成回路的边将其加入到生成树中。因此,初始化时有 |V| 棵单顶点树在森林中,当加入一条边时,两棵树就合成为一棵树。当算法完成时,就只剩下一棵树,该树即为最小生成树。
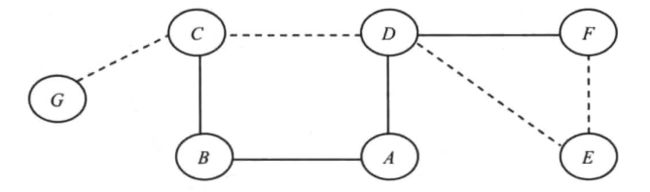
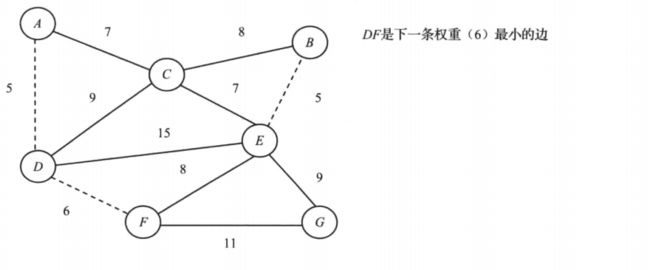
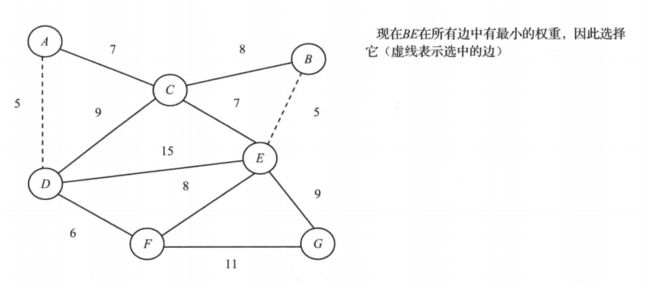
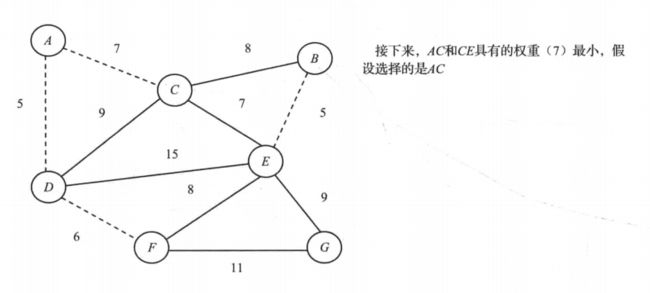
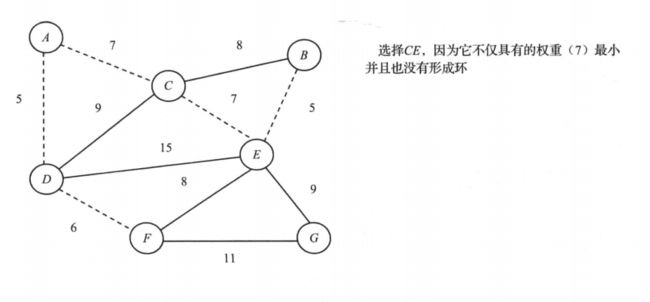
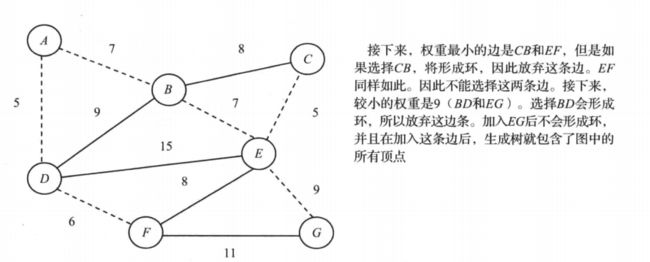
- 举例:如图6-1所示,图中各边的数值表示相应边的权重。
①
②
③
④
⑤
⑥