归并排序和快速排序类似,都典型以递归方式实现的算法,归并排序的时间复杂度分析也和快速排序的时间复杂度分析类似。本文主要介绍归并排序算法基本原理,定性分析归并排序的时间复杂度以及给出java代码实现。
一丶归并排序算法基本原理
在介绍归并排序算法之间,需要分析一个特殊排序的例子——假设存在数组A和数组B,A和B都是顺序排序的,现在需要将这两个顺序排序的数组进行合并得到数组C,并且保证合并后数组有序。
int [] A = new int[]{4,5,6,10,12,17};
int [] B = newint[]{1,3,8,9,15,20,32,50};
由于数组A和数组B都是排序数组,所以合并这两个数组,并且保持有序是可以在线性时间完成的,上述的合并排序过程用代码描述如下:
int indexA = 0;
int indexB=0;
int [] C = new int[indexA.length+B.length];
int indexC=0;
while(indexA通过分析上述代码的实现过程,只要数组A和数组B是排序数组,那么在线性时间内可以完成两个数组的合并,并且保证。
如果理解了上述排序的过程的话,其实对归并排序的理解已经完成了一大部分了,上述排序的过程就是归并排序算法中的核心,假面我们通过一个例子来观察归并排序的实现过程。假设待排序数组A满足:
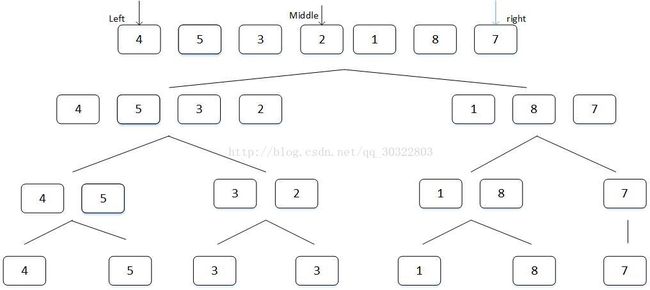
int[] A= new int[]{4,5,3,2,1,8,7};
- 图1所示代表对待排序数组进行细分的结构,上述细分结构非常有讲究,在图1中最低层的元素都是单个元素为一组,单个元素也可以看成一个排序数组。那么对同一个父节点下的两个排序数组进行上文中描述的合并操作就可以完成阶段性的排序,合并的结果如下:
-
图2中显示了对细分数组的最底层进行的合并操作结果,通过上述合并操作后,不难发现,倒数第二层每个细分数组都满足顺序性了,所以接着对倒数第二层细分数组重复步骤1中的合并操作,结果如下图所示。
-
图3中显示了对细分数组的倒数第二层进行合并操作结果,通过上述合并操作后发现,到处第三层的每个细分数组都满足顺序性了,同理重复步骤1中的合并操作,完成对整个数组的排序。
上述三个步骤就是利用归并排序对数组进行排序的过程,从上述分析角度可以看出归并排序是一个明显的递归排序算法,其核心操作是对两个顺序的子数组进行合并操作。
二丶归并排序算法的时间复杂度分析
定性的分析归并排序的时间复杂度:长度为N的待排序数组,依据上文中的细分结构,最多能被分成Log(N)层。每层的子数组都会进行合并操作,每层比较的总次数都是N。所以时间复杂是Nlog(N)。
定量分析归并排序的时间复杂度:归并排序的时间复杂度分析是典型的递归时间复杂度分析的例程,这里用简单的篇幅描述一下定量分析递归算法时间复杂度的过程。
将对长度为N的数组进行递归排序的时间消耗记T(N),同时假设N是偶数。那么依据递归排序的过程T(N)可如下计算:
T(N)=2T(N/2)+N (1)
方程两边同时除以N,得到下式:
T(N))/N=T(N/2)/(N/2)+1 (2)
对于式2而言,利用N=依次带入可得:
T(N/2))/(N/2)=T(N/4)/(N/4)+1 (3)
T(N/4))/(N/4)=T(N/8)/(N/8)+1 (4)
⋮
T(2))/2=T(1)/1+1(LogN+3) (LogN+1)
将式(2)到式(LogN+1)依次相加起来,可得:
T(N))/N=T(1)/1+logN (LogN+2)
(N)=N+NlogN=O(NlogN) (LogN+3)
通过上述计算可以清晰的看到归并排序的时间复杂度分析过程。
三丶归并排序的java代码实现
public class Solution {
/*
* @param A:an integer array
* @return:
*/
public voidsortIntegers2(int[] A) {
// writeyour code here
//利用归并排序对数组A进行排序
mergeSort(A,0,A.length-1);
}
//归并排序
public void mergeSort(int[] A,int start,int end){
if(start>=end) return;
int middle= (start+end)/2;
mergeSort(A,start,middle);
mergeSort(A,middle+1,end);
//归并排序需要分配的临时数组
//这是归并排序的核心
int []temp = new int[end-start+1];
inti=start;
int j =middle+1;
intindex=0;
while(i<=middle&&j<=end){
if(A[i]<=A[j]){
temp[index++] = A[i++];
}else{
temp[index++] = A[j++];
}
}
while(i<=middle){
temp[index++] =A[i++];
}
while(j<=end){
temp[index++] =A[j++];
}
i=start;
index = 0;
for(;i<=end;i++){
A[i] =temp[index++];
}
}
}
Reference:
[1] 数据结构与算法java语言描述版
[2]原文博客博客链接