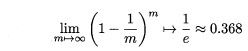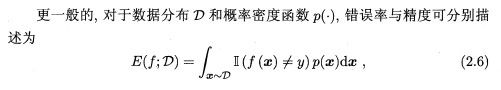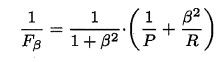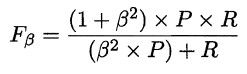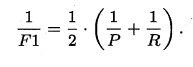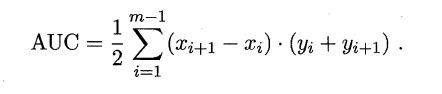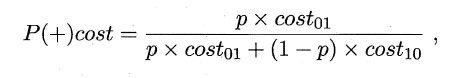第2章 模型评估与选择
2.1经验误差与过拟合
①误差(error):学习器的预测输出与样本的真实输出之间的差异
②训练误差(training error)或经验误差(empirical error):在训练集上的误差
③测试误差(test error):在测试集上的误差
④泛化误差(generalization error):学习器在所有新样本上的误差
⑤过拟合(overfitting):学习能力过于强大,把训练样本自身的一些特点当成所有潜在样本都会有的一般性质,导致泛化能力下降
⑥欠拟合(underfitting):学习能力太差,对训练样本的一般性质尚未学好 在过拟合问题中,训练误差很小,但测试误差很大;在欠拟合问题中,训练误差和测试误差都比较大。目前,欠拟合问题容易克服,如在决策树中扩展分支,在神经网络中增加训练轮数;但过拟合问题是机器学习面临的关键障碍。
⑦模型选择:在理想状态下,选择泛化误差最小的学习器。
2.2评估方法
通常,我们可通过实验测试来对学习器的泛化误差进行评估而做出选择。为此,需要使用一个“测试集”来测试学习器对新样本的判别能力,然后用测试集的“测试误差”作为泛化误差的近似,需要注意的是测试集应该尽可能与训练集互斥。在包含m个样例的数据集D中得到训练集S和测试集T,有以下几种方法:
2.2.1留出法
将数据集D划分为两个互斥的集合,一个作为训练集S,一个作为测试集T,即D=S∪T且S∩T=∅。需要注意的是:训练/测试集的划分要尽可能保持数据分布的一致性,避免因数据划分过程引入额外的偏差而对最终结果产生影响,一般采用分层抽样,保持样本类别比例相似。但单次留出法得到的结果往往不够稳定可靠,一般要采用若干次随机划分,重复实验评估后取平均值作为留出法最后的结果。常用的划分为:大约2/3-4/5的样本用于训练,剩下的用于测试。
2.2.2交叉验证法(k折交叉验证)
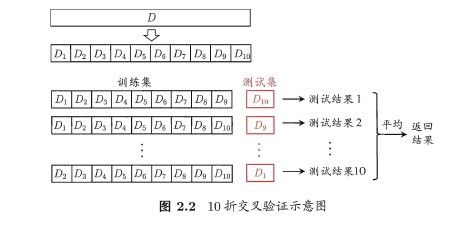
将数据集D划分为k个大小相同的互斥子集,即D=D1∪D2∪…∪Dk,Di∩Dj=∅(i≠j),同样为尽可能保持数据分布的一致性,采用分层抽样的方法获得这些子集。交叉验证法的思想是:每次用k-1个子集的并集作为训练集,余下的那个子集作为测试集,这样就有k种训练/测试集划分的情况,从而可进行k次训练和测试,最终返回k次测试结果的均值。交叉验证法评估结果的稳定性很大程度上取决于k的取值,k最常用的取值是10,此时称为10折交叉验证,示意图如下:
与留出法类似,将数据集D划分为k个子集存在多种划分方式,因此要随机使用不同的划分重复p次,最终的评估结果是这p次k折交叉验证结果的均值,常见的是10次10折交叉验证。特殊地,当k=m时,划分的k个子集的每个子集中只有一个样本,称为“留一法”,留一法中被实际评估的模型与期望评估的用D训练出的模型相似,因此,其评估结果比较准确,但计算机的开销是巨大的。
2.2.3自助法
给定包含m个样本的数据集D,每次随机从D 中挑选一个样本,将其拷贝放入D’,然后再将该样本放回初始数据集D 中,使得该样本在下次采样时仍有可能被采到。重复执行m 次,就可以得到了包含m个样本的数据集D’。可以得知在m次采样中,样本始终不被采到的概率取极限为:
即通过自助采样,初始样本集D中大约有36.8%的样本没有出现在D’中,于是可以将D’作为训练集,D-D’作为测试集。自助法在数据集较小,难以有效划分训练/测试集时很有用,然而自助法产生的数据集(随机抽样)改变了初始数据集的分布,这会引入估计偏差。因此,在初始数据量足够时,留出法和交叉验证法更常用。
2.2.4调参和最终模型
大多数学习算法都有些参数(parameter) 需要设定,参数配置不同,学得模型的性能往往有显著差别,这就是通常所说的”参数调节”,简称”调参” (parameter tuning)。学习算法的很多参数是在实数范围内取值,因此,对每种参数取值都训练出模型来是不可行的。常用的做法是对每个参数选定一个范围和步长λ。简单估计一下:假定算法有3 个参数,每个参数仅考虑5 个候选值,这样对每一组训练/测试集就有5*5*5= 125 个模型需考察,很多学习算法有不少参数需要设定,工程量浩大,参数调得好不好对最终模型的性能有关键影响。另外,需注意的是,当选定好模型和调参完成后,应该用初始数据集D重新训练模型,即让最初划分出来用于评估的测试集也被模型学习,增强模型的学习效果。
2.3性能度量
①性能度量(performance measure):衡量模型泛化能力的评价标准,在对比不同模型的能力时,使用不同的性能度量往往会导致不同的评判结果。
②均方误差(mean squared error):回归任务中最常用的性能度量。
2.3.1错误率和精度
在分类任务中,即预测离散值的问题,最常用的两种性能度量,错误率是分类错误的样本数占样本总数的比例,精度则是分类正确的样本数占样本总数的比例,错误率+精度=1。
2.3.2查准率/查全率/F1
错误率和精度虽常用,但不能满足所有的需求,例如:在信息检索中,我们经常关心检索出的信息中有多少是用户感兴趣的(即查准率: precision),或者说用户感兴趣的信息中有多少被检索出来了(即查全率:recall)。因此,使用查准/查全率更适合此类需求的性能度量。对于二分类问题,分类结果混淆矩阵与查准/查全率定义如下:
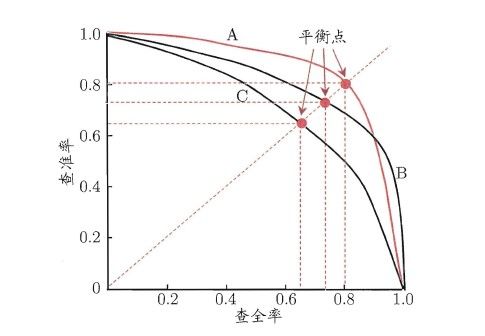
查准率与查全率是一对矛盾的度量。一般来说,查准率越高时,查全率往往偏低;而查全率高时,查准率往往偏低。例如我们想让检索出的内容尽可能用户全都感兴趣,那只能检索我们把握高的内容,这样就漏掉了一些用户感兴趣的内容,查全率就低了;如果想让用户感兴趣的内容都被检索出来,那只有将所有内容都检索出,这样查准率就很低了。“P-R曲线”是描述查准/查全率变化的曲线,P-R曲线定义如下:根据学习器的预测结果(一般为一个实值或概率)对测试样本进行排序,将"最可能"是正例的样本排在前面,"最不可能"是正例的排在后面,按此顺序逐个把样本作为正例进行预测,每次计算出当前的P值和R值,如下图所示:
若一个学习器C的P-R曲线被另一个学习器A的P-R曲线完全包住,可称学习器A的性能优于学习器C。若两个学习器的P-R曲线发生交叉,则比较它们的面积,面积大的性能优。但一般来说,面积很难估算,因此衍生了“平衡点”(Break-Event Point,简称BEP),即当P=R时的取值,平衡点的取值越高,性能越优。 P和R指标有时会出现矛盾的情况,这样就需要综合考虑他们,最常见的方法就是F-Measure,又称F-Score。F-Measure是P和R的加权调和平均,即:
特别地,当β=1时,也就是常见的F1度量,是P和R的调和平均,当F1较高时,模型的性能越好。
有时候我们会有多个二分类混淆矩阵,例如:多次训练或者在多个数据集上训练,那么估算全局性能的方法有两种,分为宏观和微观。简单理解,宏观就是先算出每个混淆矩阵的P值和R值,然后取得平均P值macro-P和平均R值macro-R,再算出Fβ或F1,而微观则是计算出混淆矩阵的平均TP、FP、TN、FN,接着进行计算P、R,进而求出Fβ或F1。
2.3.3 ROC与AUC
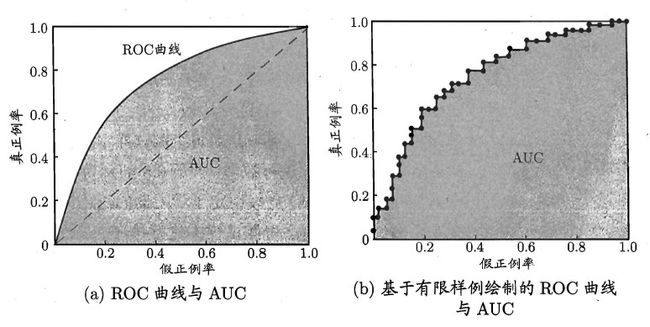
学习器对测试样本的评估结果一般为一个实值或概率,设定一个阈值,大于阈值为正例,小于阈值为负例,因此这个实值的好坏直接决定了学习器的泛化性能,若将这些实值排序,则排序的好坏决定了学习器的性能高低。ROC曲线正是从这个角度出发来研究学习器的泛化性能,ROC(Receiver Operating Characteristic)曲线与P-R曲线十分类似,都是按照排序的顺序逐一按照正例预测,不同的是ROC曲线以“真正例率”(True Positive Rate,简称TPR)为横轴,纵轴为“假正例率”(False Positive Rate,简称FPR),ROC偏重研究基于测试样本评估值的排序好坏。
现实任务中通常利用有限个测试样例来绘制ROC图,无法产生(a)中的光滑曲线,只能绘制出如图(b)的近似ROC曲线。绘制过程如下:给定m+个正例和m-个反例,根据学习器预测结果对样例进行排序,然后把分类阈值设为最大,即把所有样本都预测为反例,真正例率和假正例率均为0,在坐标(0,0)处标记一个点。然后,将分类阈值依次设为每个样例的预测值,即依次将每个样例划分为正例。设前一个标记点坐标为(x,y),当前若为真正例,则对应标记点的坐标为(x,y+1/m+);若当前为假正例,则对应标记点的坐标为(x+1/m-,y),然后用线段连接相邻点即可。进行学习器的比较时,与P-R图相似。ROC曲线下的面积定义为AUC(Area Under ROC Curve),不同于P-R图,这里的AUC是可计算的,即曲线下每一个小矩形的面积之和。AUC越大,证明排序的质量越好,AUC=1,表示所有正例排在负例前面,AUC=0则相反。
2.3.4 代价敏感错误率与代价曲线
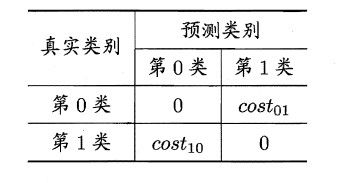
为权衡不同类型错误所造成的不同损失,可为错误赋予“非均等代价”(unequal cost)。以二分类任务为例,设定一个“代价矩阵(cost matrix)”,cost_ij表示将第i类样本预测为第j类样本的代价,一般来说,损失程度相差越大,cost01和cost10值的差别越大。如下:
在非均等错误代价下,我们希望最小化总体代价(total cost),则“代价敏感(cost-sensitive)”的错误率为
在非均等错误代价下,ROC曲线不能直接反映出学习器的期望总体代价,而“代价曲线”可达到目的。代价曲线横轴是取值在[0,1]之间的正例概率代价
其中p表示正例的概率,纵轴是取值为[0,1]的归一化代价。
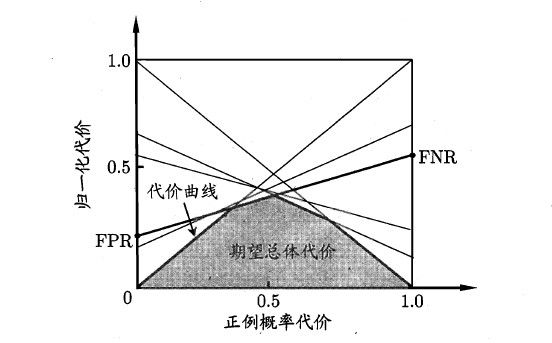
代价曲线的绘制很简单:设ROC曲线上点的坐标为(TPR,FPR) ,则可相应计算出FNR=1-TPR,然后在代价平面上绘制一条从(0,FPR) 到(1,FNR) 的线段,线段下的面积即表示了该条件下的期望总体代价;如此将ROC 曲线土的每个点转化为代价平面上的一条线段,然后取所有线段的下界,围成的面积即为在所有条件下学习器的期望总体代价,如图所示: