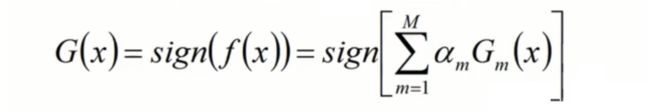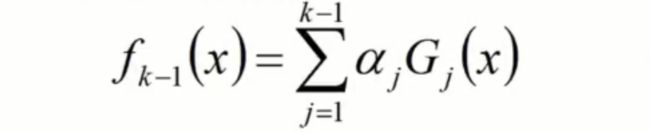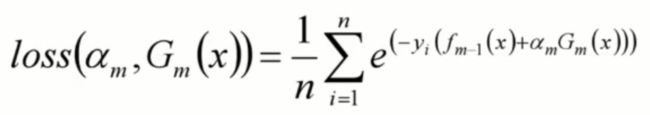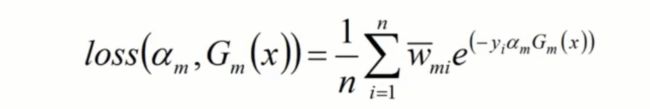02 集成学习 - 特征重要度、Extra Tree、TRTE、IForest、随机森林总结
八、Boosting 提升学习
提升学习是一种机器学习技术,可以用于回归和分类问题。它每一步产生弱预测模型 (如决策树),并加权累加到总模型中。如果每一步的弱预测模型的生成都是依据损失函数的梯度方式的,那么称为梯度提升(Gradient Boosting)。
提升技术的意义: 如果一个问题存在弱预测模型,那么可以通过Boosting技术得到一个强预测模型。
常见的模型有: Adaboost、Gradient Boosting(GBT/GBDT/GBRT)、XGBoost、LightGBM。
不同模型在Boosting处理过程中的差异体现在根据效果更改数据这一步。
回顾: 随机森林算法
1、随机有放回抽样,选取S个数据集,建立S个模型。
2、在每一个基模型构建过程中,对于划分决策树时,随机选择K个特征进行划分。
随机森林算法本身(bagging方法),不会对原有数据集中的数据内容进行改变,只是对数据集进行随机抽样。
01 集成学习 - 概述、Bagging - 随机森林、袋外错误率
提升学习算法:
bagging算法不会更改原有数据的值,但是在Boosting算法中会根据模型训练的结果,通过某种算法,对原有数据的值进行更改,再建立下一个模型。
九、AdaBoost算法原理
百度百科说得挺好:
https://baike.baidu.com/item/adaboost/4531273?fr=aladdin
Adaptive Boost 是一种迭代算法。每一轮迭代后生成一个新的学习器,然后对样本进行预测。 预测对的权重减小,预测错的权重增加。权重越高在下一轮的迭代中占的比重就越大,即越难区分的样本在样本中会越重要。
整个迭代当错误率足够小,或迭代次数到一定次数停止。
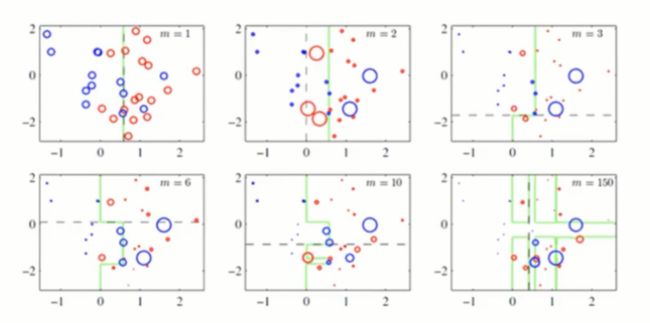
下图虚线代表每次预测的分割线,预测成功的点会变小,预测失败的点会变大。一共进行了6次迭代。
上述是对样本层面的调整,下面看看对模型的调整。
注意,为了方便区分,本文对一概念做个定义上的区分:对样本比重的调整本文统称为权重,对模型比重的调整本文称为权值。
Adaboost算法将基分类器的线性组合作为强分类器,同时给分类误差率较小的基分类器以大的权值,给分类误差率较大的基分类器以小的权值。构建的线性组合为:
GmG(x): 基分类器;α m : 权值;
最终分类器是在线性组合的基础上,f(x) 很有可能是一个连续的值,那么如果对连续值进行分类操作?我们可以用Sign函数进行转换。
补充知识:
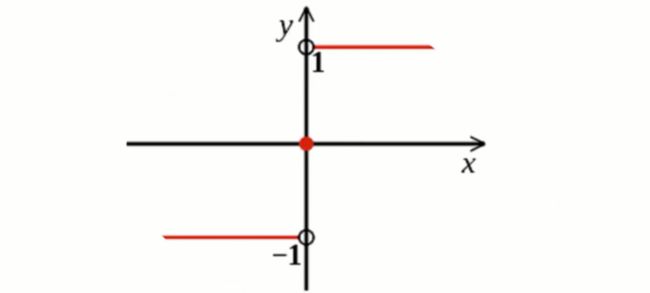
sign(x)或者Sign(x)叫做符号函数,在数学和计算机运算中,其功能是取某个数的符号(正或负):
当x>0,sign(x)=1; 当x=0,sign(x)=0; 当x<0, sign(x)=-1;
f(x)可能是连续值,经过sign函数处理后,最终得到的G(x)的取值不是1就是-1。这是Adaboost算法中必要重要的一环,目前对于Adaboost算法了解到这个程度即可。
最终强学习器G(x)的损失函数:
损失函数(代价函数越小越好),反应了模型的好坏。这是一个示性函数(0,1损失函数)。
考虑单个样本的情况:即当满足 G(x)≠y 时,说明预测错了取1。G(x)=y,说明预测对了取0。
最后累加n个样本对应的取值,求平均值。
如果4个样本,最后I(G(x)≠y) 计算后的值分别问:0,0,1,0;说明3个预测对了,一个预测错了,即loss=1/4;
PS:这里的取值不是连续的,下面介绍连续取值的损失函数:
解析:先来考虑单个损失情况。注意:下面这个式子是恒成立的,我们一步一步来分解该公式。
1、当预测值不等于真实值,即G(x)≠y的时候,说明真实值和预测值是异号的 => yG(x) < 0;又∵G(x) = sign(f(x)),f(x)是正的时候,G(x)=1。f(x)是负的时候,G(x)=-1。∴ f(x)和G(x)是同号的。所以 => yf(x) < 0;
2、当预测值等于真实值,即G(x)=y的时候, yf(x) > 0;
3、-yf(x) 是e指数函数的自变量。
3、观察下面e的指数函数图:
当x<0时,ex 的取值为 (0,1);
当x=0时,ex=1;
当x>0时,ex 的取值为 (1,+);
4、 结合上述公式进行推导:
令 -yG(x) = k,
当G≠y时,k>0, 得: e^k 取值 (1,+),此时 I(G≠y)=1;
当G=y时,k<0, 得: e^k 取值 (0,1),此时 I(G≠y)=0;
无论如何,I(G≠y) < e^k;
上图单个样本的恒不等式得证。
将单个样本的恒不等式进一步推演到整个样本的范围,不等式依然恒成立:
例子:
1号样本预测准确,左式=0,右式= (0,1)
2号样本预测错误,左式=1,右式= (1,+∞)
3号样本预测准确,左式=0,右式= (0,1)
1~3号样本加和,左边<右边;
最终推论: 当右边式子达到最小值的时候,左边的式子也能达到最小,此时损失函数最小。这个公式的优点在于我们能构建出一个连续的损失函数,和上面提到的0\1损失函数等价,都可以衡量系统的好坏。
进一步思考:
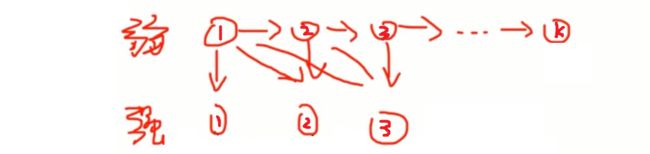
如上图所示:
第一轮:最初我们根据样本训练,得到了弱学习器①。α1×弱学习器① = 强学习器①。
第二轮:上一轮预测错误的样本加大权重,正确的缺少权重,训练得到弱学习器②。α1×弱学习器①+α2×弱学习器② = 强学习器②
....
1、第k轮的强学习器可以用k-1轮的学习器+第k轮的弱学习器×权值来代替:
2、将fk(x)代入损失函数:
3、得:由第m步生成的基模型和第m步基模型的权值两个未知量,构成的损失函数
进一步思考:
我们构建损失函数的目的是让损失函数值最小。即让上面得到的公式:由第m步生成的基模型和第m步基模型的权值两个未知量,构成的损失函数 最小。
当我们建立第m个模型的时候,前面m-1个模型必然已经构建完成。所以fm-1(x)是已知量,我们认为这部分公式是一个常数,对于求损失函数的最小值没有影响。
1、使下列公式达到最小值的αm和Gm就是AdaBoost算法的最终求解值。
2、G这个分类器在训练过程中,就是为了让误差率最小,所以可以认为G越小就是误差率约小。
其中I(y≠G)代表预测错误的次数 : 想让损失函数最小,自然意味着希望预测错误率越小越好。
ξm=P(G≠y) 是误差率,即预测值不等于真实值的概率。预测错误的个数/整个样本数量。
3、对于αm而言,通过求导然后令导数为0,可以得到公式(log对象可以以e为底也可以以2为底):
αm是第m个基学习器的权值。权值和误分率ξm有关。
(1-ξm) / ξm : 当误分率越小的时候,这个公式值越大。ln后的值也越大。αm权值也就越大。
这个思路也我们最初求权值的思想一致:要为每个基模型附权,错误率越小权值越大。
这个公式的推导过程比较复杂,暂时记住这个结论即可。
04 集成学习 - Boosting - AdaBoost算法构建