跟Python的IO读写功能一样,numpy中也有文件的读写功能,将ndarray对象也可以保存到磁盘文件并从磁盘文件加载。方便保存使用numpy编写的代码。在numpy中也有一些高级的库,今天我们这里简单讲一下矩阵库和线性代数的库,让我们更了解numpy这个模块。
一、IO操作
Numpy 可以读写磁盘上的文本数据或二进制数据。NumPy 为 ndarray 对象引入了一个简单的文件格式:npy。npy 文件用于存储重建 ndarray 所需的数据、图形、dtype 和其他信息。现在在Numpy中可用的IO功能有:
- Load()和save()函数处理numpy二进制文件(需要带npy扩展名)
- Loadtxt()和savetxt()函数处理正常的文本文件
Numpy为ndarray对象引入了一个简单的文件格式,这个npy文件在磁盘文件中,存储重建ndarray 所需的数据、图形、dtype 和其他信息,以便正确获取数组,即使该文件在具有不同架构的另一台机器上。
- numpy.save()
函数将输入的数组存储在具有npy扩展名的磁盘文件中。
为了从outfile.npy重建数组,需要使用load()函数
save() 和 load() 函数接受一个附加的布尔参数 allow_pickles。Python 中的 pickle 用于 在保存到磁盘文件或从磁盘文件读取之前,对对象进行序列化和反序列化。
2、savetxt()
函数以简单文本文件格式存储和获取数组数据,是通过 savetxt() 和 loadtx() 函数完成的。
savetxt() 和 loadtxt() 函数接受附加的可选参数,例如页首,页尾和分隔符。
二、numpy中的矩阵库
NumPy 包包含一个 Matrix 库 numpy.matlib 。此模块的函数返回矩阵而不是返回 ndarray对象。一个m*n的矩阵是一个由m行(row)n列(column)元素排列成的矩形阵列。矩阵里的元素可以是数字、符号或数学式。
- matlib.empty()
函数返回一个新的矩阵,且不初始化元素。
2、numpy.matlib.zeros()
此函数返回以0填充的矩阵。
3、numpy.matlib.ones()
此函数返回以1填充的矩阵。
4、numpy.matlib.eye()
这个函数返回一个矩阵,对角线元素为 1,其他位置为零。
5、numpy.matlib.identity()
函数返回给定大小的单位矩阵。单位矩阵是主对角线元素都为 1 的方阵。
6、numpy.matlib.rand()
函数返回给定大小的填充随机值的矩阵
在这里需要注意的是,矩阵总是二维的,而ndarray是一个n维数组,两个对象都是可以互换的,但是两个对象并不是相同的。
三、线性代数库
相信大家在学习线性代数的时候,都会觉得线性代数是非常难学的,线性代数就像一层硬纸,刚开始学习的时候是非常难以穿透的,但是只要认真的学下去,那么穿过那个点之后呢就恍然大悟,当然对线性代数掌握不是很好的人也没事,numpy中有专门的库numpy.linalg可以提供线性代数所需要的所有功能,我们可以先学习如何处理,然后在慢慢的去学习线性代数基础知识。
Numpy中提供的方法如下:
- numpy.dot() 返回两个数组的点积
- numpy.vdot() 返回两个向量的点积
- numpy.inner() 返回一维数组的向量内积
- numpy.matmul() 返回两个数组的矩阵乘积
- numpy.linalg.det() 计算输入矩阵的行列式
- numpy.linalg.solve() 求解矩阵形式的线性方程的解
- numpy.linalg.inv() 计算矩阵的逆
接下来我们就一个一个方法开始学习如何处理线性代数的方法。
1、numpy.dot()
这个函数返回两个数组的点积。对于二维向量,相当于是矩阵乘法。对于一维数组,它是向量的内积。对于 N 维数组,它是a的最后一个轴上的和与b的倒数第二个轴的乘积。
1.1什么是矩阵乘法
在这里我在带领大家复习一下什么矩阵乘法,首先在百度中矩阵乘法的定义是这样的:
矩阵相乘最重要的方法是一般矩阵乘积。它只有在第一个矩阵的列数(column)和第二个矩阵的行数(row)相同时才有意义。一般单指矩阵乘积时,指的便是一般矩阵乘积。一个m×n的矩阵就是m×n个数排成m行n列的一个数阵。由于它把许多数据紧凑的集中到了一起,所以有时候可以简便地表示一些复杂的模型。
这么看其实是比较复杂的,但是咱们分开来学,也是很简单的,假设A矩阵为m行p列,B矩阵为p行n列,矩阵相乘后,A*B=C,那么C矩阵就是m行n列,也就是说矩阵C的行数=矩阵A的行数,矩阵C的列数=矩阵B的列数,矩阵相乘就是A矩阵的行去乘以B矩阵的列。这么说可能还是有一些复杂,咱们看一下实例就能明白了。
1.2实例
在这个例子中,C矩阵的第一行第一个元素的结果是A矩阵的第一行 B矩阵的第一列,也就是11+2 13=37,第一行第二个元素的结果为112+2 14=40。第二行第一个元素为311+4 13=85,第二行第二个元素为312+4*14=92。这么看的话是不是感觉就很清楚了。
在Python的较新版本中还支持了直接使用@号作为矩阵的乘法,避免在调用numpy.dot()方法了。
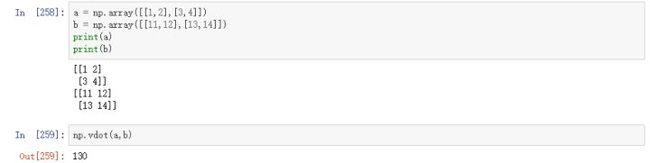
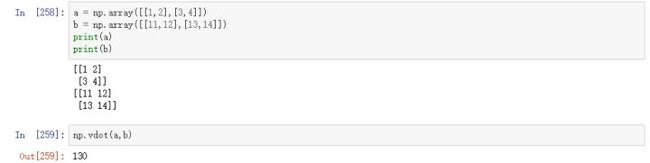
2、numpy.vdot()
这个函数返回两个向量的点积。如果第一个参数是复数,那么它的共轭复数会用于计算。如果参数是多维数组,它会被展开。
在这里看,点积也就是对应的元素相乘,也就是1 11+212+3 13+414=130,这个方法要求两个向量的元素相同不在乎行和列,如果不同的话则会报错。
3、numpy.inner()
这个函数返回一维数组的向量内积。对于更高的维度,它返回最后一个轴上的乘积的和。
3.1、一维数组
结果等价于1 0+21+3*0
3.2、二维数组
上面的列子中,内积的计算如下
Array([[111+212,113+214],
[311+412,313+414]])
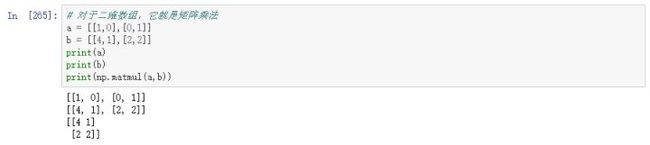
4、numpy.matmul()
这个函数结果返回两个数组的矩阵乘积。虽然它返回二维数组的正常乘积,但如果任一参数的维数大于 2,则将其视为存在于最后两个索引的矩阵的栈,并进行相应广播。另一方面,如果任一参数是一 维数组,则通过在其维度上附加 1 来将其提升为矩阵,并在乘法之后被去除。
4.1、对于二维数组来说,它就是矩阵的乘法
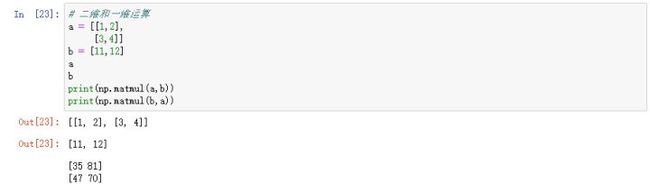
4.2、二维和一维的运算
计算的过程为:
Np.matmul(a,b)=[111+212 312+412]
Np.matmul(b,a)=[111+123 112+124]
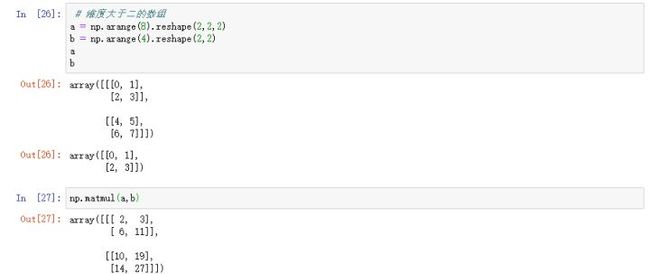
4.3、维度大于2的数组
计算过程为
Array([[[00+12,01+31],
[20+36,21+33]],
[[40+52,41+53],
[60+72,61+73]]])
5、numpy.linalg.det()
这个函数计算输入矩阵的行列式。行列式在线性代数中是非常有用的值。
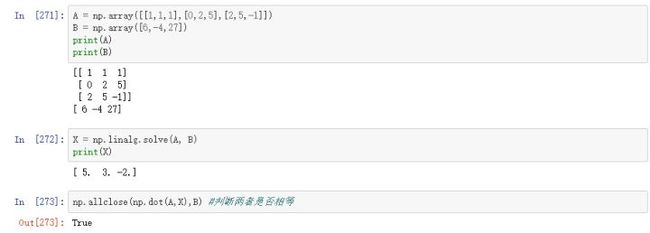
6、numpy.linalg.solve()
函数给出了矩阵形式的线性方程的解。
例如,考虑以下线性方程:
x + y + z = 6
2y + 5z = -4
2x + 5y - z = 27
可以使用矩阵表示为:
1 2 3
4 5 6 .$\left[\begin{matrix}x\y\z\end{matrix|\right]
7 8 9
$
6
-4
27
如果矩阵成为A、X和B,方程变为B
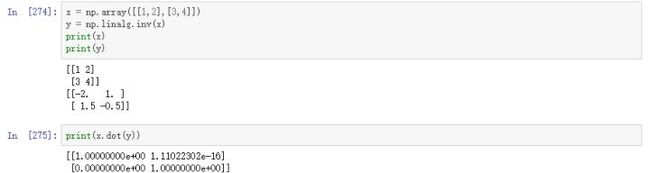
7、numpy.linalg.inv()
这个函数是用来计算矩阵的逆。