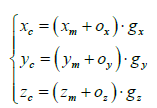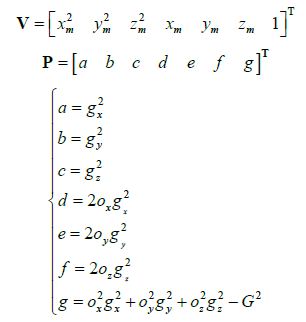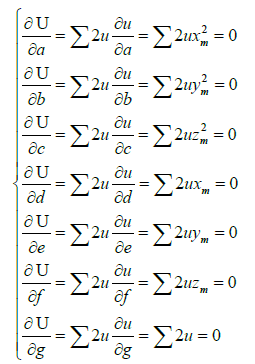罗盘和加计的校准是日常开发中最基础的工作,特邀Echo老师对罗盘和加速度计校准的工程方法进行总结,为小伙伴你们解惑,是有此文。
作者信息
Echo,本名邹佳池,从事嵌入式软件开发。
联系方式:QQ529380360
超详细讲解:罗盘和加速度计校正方法
(附C源代码)
1.为什么要校正
我们都知道,罗盘是测量周围的磁场强度,若不存在外在磁场的干扰,只存在地磁的话,理论上罗盘旋转测得的磁场是一个圆球。
可是现实空间中,除了地磁场外,还存在其他的磁场干扰,这里我索性将它分为两大类。
第一类:地球空间中的磁场,这类磁场有个特点,就是随着罗盘坐标系的转动,磁场方向不变,类似地磁场。
第二类:罗盘坐标空间中的磁场,这类磁场源一般是固定在飞机上的,所以随着罗盘坐标系的转动,磁场方向也跟着转动。但是对于罗盘坐标系来说,却是一个恒定值。
对于第一类的磁场,目前我了解到的还没有什么好的方式可以进行校正(如果哪位大神知道,还请告知)。而我后面要介绍的校正方法,即是滤除第二类磁场的干扰,校正的思想即是基于最小二乘法的椭球拟合算法。
注:这个只能校正磁场强度固定不变的磁场,而对于电机这种变化的磁场,我没有测验过,不知道电机产生磁场的强度大小跟电机转速的关系怎样,如果谁有研究过的,还请告知,谢谢。
2.椭球拟合校正理论推导
网络上有许多关于椭球拟合校正的论文,我都没有细看,因为那些公式都写得晦涩难懂,没有那个耐心,我这里尽量用最简洁的语言介绍校正方法的理论基础。
首先建立数值模型,设测量值为:
,校正后的值为:,
平移参数为:
缩放参数为:
他们之间的关系如下所示:
我们校正后的目标就是使得校正值近似分布在一个圆球上,而圆球的公式大家都知道:x2+y2+z2=R2,故我们将校正后的值带入圆球公式,与理论的圆球半径平方做差,构建误差u:
将校正值用测量值替换,变为:
可以看到,这分明就是个椭圆公式嘛~
记:
则我们的误差u可以写为如下形式:
下面就是校正的核心思想了:假设我们有许多组数据,我们要求得一组参数,使得所有数据的误差和最小,即∑u最小,但是由于u有正有负,所以符号相反的误差有可能相互抵消。那么加绝对值呢?这个也不可取,因为对绝对值函数求极小值十分复杂。那么我们自然就想到对u求平方和,即:
U=∑u^2
我们把u看成一个未知数,这个函数是一个二次函数,其有极小值点。而为了求得这个极小值点,我们对其做偏导即可:
记:
则我们可以将偏导写成如下形式:
B是已知的,P是我们待求的参数矩阵,故可以通过求齐次线性方程组,来求得P的各个参数的解。
齐次线性方程组求解的过程我这里就不详细解释了,我算法中使用的方法是经典的高斯消元法,有兴趣的可以仔细看看。
当我们求得P的各个未知数a,b,c,d,e,f,g后,需要通过这几个参数反求出我们的偏移量(ox,oy,oz)和缩放量(gx,gy,gz)。
在反求解之前,我们先回到上一个式子,BxP=0。其实满足这个式子的解P有无数组,我们可以将式子改写成BxCP=0,C是一个任意常数,即
我们通过解线性方程组求得的只是这个解系中的一个基本解,所以我们首先要求出这个基本解的C。
其算式经推导如下,带入a,b,c,d,e,f,g即可求解:
C=(d2/a + e2/b + f2/c - 4g)/4R2 (R为理论圆球半径)
ox=d/2a
oy=e/2b
oz=f/2c
gx=sqrt(a/C)
gy=sqrt(b/C)
gz=sqrt(c/C)
最后,将这六个参数回调到之前的式子中去,即完成校正。
3.校正程序源码(C语言)
代码太长了 就不贴出来了,放在网盘种大家下载
罗盘与加计校准方法 C源代码
http://pan.baidu.com/s/1dFiB6z3
............