三羊献瑞
public class test0406 {
//祥瑞生辉三洋献气 01234567
public static int a[]=new int[8];
public static int visited[]=new int[10];
public static void dfs(int cur){
if(cur==8){
int x,y,z;
x=a[0]*1000+a[1]*100+a[2]*10+a[3];
y=a[4]*1000+a[5]*100+a[6]*10+a[1];
z=a[4]*10000+a[5]*1000+a[2]*100+a[1]*10+a[7];
if(x+y==z){
System.out.println(y);
}
return;
}
for(int i=0;i<=9;i++){
if(cur==0&&i==0)
continue;
if(cur==4&&i!=1)
continue;
if(visited[i]==0){
visited[i]=1;
a[cur]=i;
dfs(cur+1);
visited[i]=0;
}
}
}
public static void main(String[] args){
dfs(0);
}
}
牌型种数
小明被劫持到X赌城,被迫与其他3人玩牌。
一副扑克牌(去掉大小王牌,共52张),均匀发给4个人,每个人13张。
这时,小明脑子里突然冒出一个问题:
如果不考虑花色,只考虑点数,也不考虑自己得到的牌的先后顺序,自己手里能拿到的初始牌型组合一共有多少种呢?
思路:循环遍历每个点数所选择的张数,每个点数最多可以选4张,最少可以选0张即不选,每当牌总数达到13张则计数。
变量cur代表对1-13这13个牌种的遍历,每个牌种的选择从0到4,最终需要13张全部遍历完成
变量sum代表这十三个牌种的总和,最后需要=13
public class test0406oj2 {
public static int N=0;
public static void dfs(int cur,int sum){
if(cur>13)
return;
if(sum>13)
return;
if(sum==13&&cur==13){
N++;
}
for(int i=0;i<=4;i++){
dfs(cur+1,sum+i);
}
}
public static void main(String[] args){
dfs(0,0);
System.out.println(N);
}
}
寒假作业
现在小学的数学题目也不是那么好玩的。
看看这个寒假作业:
□ + □ = □
□ - □ = □
□ × □ = □
□ ÷ □ = □
每个方块代表1~13中的某一个数字,但不能重复。
比如:
6 + 7 = 13
9 - 8 = 1
3 * 4 = 12
10 / 2 = 5
以及:
7 + 6 = 13
9 - 8 = 1
3 * 4 = 12
10 / 2 = 5
就算两种解法。(加法,乘法交换律后算不同的方案)
你一共找到了多少种方案?
每个数的选择范围1到13 进行比较
这种方法用时较长
public class oj3 {
public static int ans=0;
public static int a[]=new int[20];
public static int visited[]=new int[20];
public static void dfs(int cur){
if(cur>12){
if((a[1]+a[2]==a[3])&&
(a[4]-a[5]==a[6])&&
(a[7]*a[8]==a[9])&&
(a[11]*a[12]==a[10]))
ans++;
return;
}
for(int i=1;i<=13;i++){
if(visited[i]==0){
visited[i]=1;
a[cur]=i;
dfs(cur+1);
visited[i]=0;
}
}
}
public static void main(String[] args){
dfs(1);
System.out.println(ans);
}
}
对3,6,9均进行判断,用时较短
public class test0602 {
public static int a[]=new int[14];
public static int visit[]=new int[14];
public static int sum=0;
public static void main(String[] args){
dfs(1);
System.out.println(sum);
}
public static void dfs(int n)
{
if(n>3 && a[1]+a[2]!=a[3])
return;
if(n>6 && a[4]-a[5]!=a[6])
return;
if(n>9 && a[7]*a[8]!=a[9])
return;
if(n>12 && a[12]*a[11]==a[10])
{
sum++;
return;
}
for(int i=1;i<14;i++)
{
if(visit[i]==0)
{
visit[i]=1;
a[n]=i;
dfs(n+1);
visit[i]=0;
}
}
return;
}
}
剪邮票
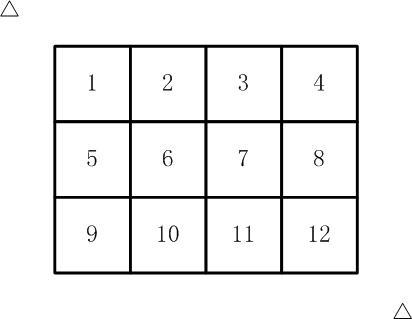
如图1, 有12张连在一起的12生肖的邮票。现在你要从中剪下5张来,要求必须是连着的。
图1.jpg
(仅仅连接一个角不算相连)比如,【图2.jpg】,【图3.jpg】中,粉红色所示部分就是合格的剪取。
图2.jpg
图3.jpg
请你计算,一共有多少种不同的剪取方法。请填写表示方案数目的整数。
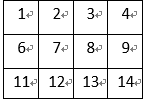
若要剪出的纸片相连,必须是某个数的上方下方左方和右方,而该纸片一共有3行4列,并且数字是连续的,我们可以通过-4,+4,-1,+1 来分别表示上下左右,但是我们发现4,8,12号数字+1到了另一行的另外一边而不连续,5,9两个数字-1也是同样,所以我们把第二行换成6,7,8,9 第三行换成11,12,13,14,从而避免出现以上的情况如图所示
public class Seven {
public static int count = 0 ; //记录总的方案数
public static int cut[] = new int[5] ; //从所有邮编中选出5张从小到大号码不同的邮票,存入该数组中避免选取的邮票出现重复
public static int isVisit[] = new int[5] ; //判断取出的5张邮票是否已经访问
public static int b[] = {+1,-1,+5,-5} ; //判断取出的5张邮票是否相连,+1表示与右边相连,-1表示左边,+5表示下面,-5表示上面
public static void main(String[] args) {
int stamp[] = new int[12] ; //定义所有邮票号码
for(int i = 1,k = 1 ; i <= 12 ; i++){ //初始化所有的邮票号码为{1,2,3,4,6,7,8,9,11,12,13,15}
stamp[i-1] = k++ ;
if(i % 4 == 0){
k ++ ;
}
}
for(int a = 0 ; a < 12 ; a++){ //通过for循环取出5张邮票,号码从小到大
for(int b = a + 1 ; b < 12 ; b++){
for(int c = b + 1 ; c < 12 ; c ++){
for(int d = c + 1 ; d < 12 ; d++){
for(int e = d + 1 ; e < 12 ; e ++){
//将取出的邮票存入cut数组中,保存
cut[0] = stamp[a] ;
cut[1] = stamp[b] ;
cut[2] = stamp[c] ;
cut[3] = stamp[d] ;
cut[4] = stamp[e] ;
for(int i = 0 ; i < 5 ; i++){ //初始化取出的邮票都为未访问状态
isVisit[i] = 0 ;
}
//开始访问
isVisit[0] = 1 ; //另cut数组头为已访问状态
//从cut数组头开始,判断该方案是否可行
find(0) ;
int flag = 1 ; //当flag为1时可行,否则不可行
for(int j = 0 ; j < 5 ; j++){
if(isVisit[j] == 0){ //只要一个数未访问到则说明不可行
flag = 0 ;
break ;
}
}
if(flag == 1){
count ++ ;
}
}
}
}
}
}
System.out.println(count);
}
private static void find(int index) {
for(int i = 0 ; i < 4 ; i++){ //计算出cut[index]上下左右的数
int tempCut = cut[index] + b[i] ;
if(tempCut < 1 || tempCut > 14 || tempCut ==5 ||tempCut==10){
continue ;
}
for(int k = 0 ; k < 5 ; k++){
if(isVisit[k]==0&&cut[k]==tempCut){//如果cut数组里有数与tempCut匹配的话,继续查询下一个
isVisit[k] = 1 ;
find(k) ;
}
}
}
}
}
神奇算式
由4个不同的数字,组成的一个乘法算式,它们的乘积仍然由这4个数字组成。
比如:
210 x 6 = 1260
8 x 473 = 3784
27 x 81 = 2187
都符合要求。
如果满足乘法交换律的算式算作同一种情况,那么,包含上边已列出的3种情况,一共有多少种满足要求的算式。
暴力方法:
import java.util.ArrayList;
import java.util.Scanner;
public class shenqisuanshibaoli {
public static int ans1=0,ans2=0;//1对3和2对2两种情况,2对2会出现交换律,最后记得除以二
public static boolean testself(int n){//使自身不重复
String s=n+"";
for(int i=1;i arr=new ArrayList<>();
for(int i=0;i arr=new ArrayList<>();
for(int i=0;i dfs方法
public class shenqisuanshi {
public static int ans=0,ans2=0;
public static int a[]=new int[10];
public static int visited[]=new int[10];
public static boolean testrepeat(){
int left=a[0];
int right=a[1]*100+a[2]*10+a[3];
int answer=left*right;
String s1=left+"";
String s2=right+"";
String s3=answer+"";
ArrayList arr=new ArrayList<>();
for(int i=0;i arr=new ArrayList<>();
for(int i=0;i3){
if(testrepeat()){
System.out.println(a[0]+"*"+a[1]+a[2]+a[3]);
ans++;
}
if(testrepeat2()){
System.out.println(a[0]+""+a[1]+"*"+a[2]+a[3]);
ans2++;
}
return;
}
for(int i=0;i<10;i++){
// if(cur==1&&i==0)
// continue;
if(visited[i]==0){
visited[i]=1;
a[cur]=i;
dfs(cur+1);
visited[i]=0;
}
}
}
public static void main(String[] args){
dfs(0);
System.out.println(ans+ans2/2);
}
}
李白打酒
话说大诗人李白,一生好饮。幸好他从不开车。
一天,他提着酒壶,从家里出来,酒壶中有酒2斗。他边走边唱:
无事街上走,提壶去打酒。
逢店加一倍,遇花喝一斗。
这一路上,他一共遇到店5次,遇到花10次,已知最后一次遇到的是花,他正好把酒喝光了。
请你计算李白遇到店和花的次序,可以把遇店记为a,遇花记为b。则:babaabbabbabbbb 就是合理的次序。像这样的答案一共有多少呢?请你计算出所有可能方案的个数(包含题目给出的)。
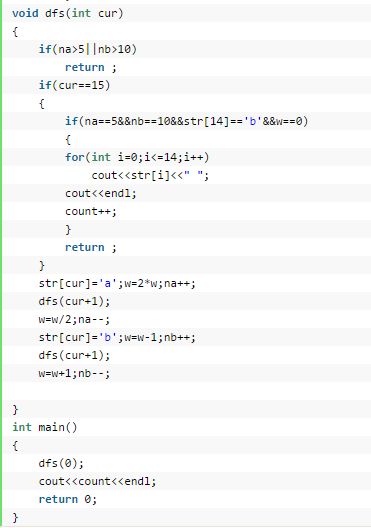
变量只有A,B 每次决定添加A还是B,设置限制条件,5,10,15,因为只有2个所以不进行for循环直接递归调用。
public class libaidajiu {
public static char[] a=new char[20];
public static int ans=0;
public static void dfs(int cur,int dian,int hua,int jiu){
if(dian>5)
return;
if(hua>10)
return;
if(cur==15){
if(dian==5&&hua==10&&a[14]=='b'&&jiu==0){
for(int i=0;i<=14;i++)
System.out.print(a[i]);
System.out.println();
ans++;
}
return;
}
a[cur]='a';
dfs(cur+1,dian+1,hua,jiu*2);
a[cur]='b';
dfs(cur+1,dian,hua+1,jiu-1);
}
public static void main(String[] args){
dfs(0,0,0,2);
System.out.println(ans);
}
}
这两者思路是一样的,贴上来这种手动更改的更方便理解。将需要来回变化的变量放参数中明显更方便。(如果不理解可以看下一题)
奇怪的比赛
某电视台举办了低碳生活大奖赛。题目的计分规则相当奇怪:
每位选手需要回答10个问题(其编号为1到10),越后面越有难度。答对的,当前分数翻倍;答错了则扣掉与题号相同的分数(选手必须回答问题,不回答按错误处理)。
每位选手都有一个起步的分数为10分。
某获胜选手最终得分刚好是100分,如果不让你看比赛过程,你能推断出他(她)哪个题目答对了,哪个题目答错了吗?
如果把答对的记为1,答错的记为0,则10个题目的回答情况可以用仅含有1和0的串来表示。例如:0010110011 就是可能的情况。
你的任务是算出所有可能情况。每个答案占一行。
public class qiguadebisai {
public static int[] a=new int[20];
public static int ans=0;
public static void dfs(int cur,int score){
if(cur>10){
if(score==100){
for(int i=1;i猜算式
public class caisuanshi {
static int[] aaa=new int[10];
public static void main(String[] args){
for(int i=100;i<=999;i++)
for(int j=100;j<=999;j++){
int x=i*j;
int a=i*(j%10);
int b=i*((j/10)%10);
int c=i*(j/100);
for(int p=0;p=1000||b>=1000||c>=1000||x>=100000||a<100||b<100||c<100)
continue;
check(x);check(i);check(j);
check(a);check(b);check(c);
boolean flag=true;
for(int p=0;p0){
aaa[n%10]++;
n=n/10;
}
}
}