Density Estimation
这个章节主要讲述了非监督机器学习中的异常检测算法(anomaly algorithm),其原理实际是利用了在工程、产品的检测中,大部分正常产品的各个feature是服从正态分布(高斯分布)的,所以给定一个样本,我们可以计算其各个feature为正常值的概率,并设定一个阈值ɛ,当样本为正常值的概率P大于ɛ时,我们就认为是正常的,当这个P小于ɛ时我们就认为其是异常的。
关于density estimation的解释可以参考wiki - density estimation
Problem Motivation
作者在这一小节主要讲了一些实际应用的例子。
- 飞机引擎检测
- 欺诈用户
- 数据中心的异常检测
Gaussian Distribution
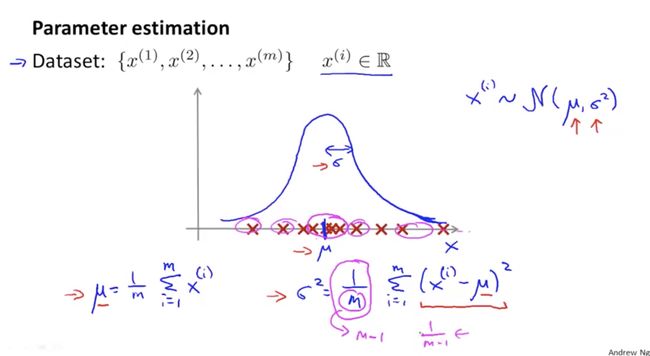
这一小节主要讲高斯分布,重点就是下图中的公式和高斯分布图:
高斯密度函数中有两个需要计算的值,一个是均值μ,另一个是平方差2,其计算公式如下:
Algorithm
前面我们已经说了,重点是计算样本为正常值的概率P,其计算就需要如下公式:
- 针对每一个feature的维度都需要进行高斯计算,从而算出μ和2,然后针对不同的样本x来计算出P
- 这里引入了一个新的数学符号Π,这是意味着相乘的关系
那么,整个异常检测算法的流程如下:
Building an Anomaly Detection System
这个章节重点讲了工程实践中具体是怎么训练我们的模型。
Developing and evaluating an anomaly detection system
首先,作者将了如何将我们的样本分为training set, cross validation set和testing set,举例如下:
- 要将异常样本放到CV和test集中
那么最终这个ɛ如何选择呢?重点就是要根据我们的precision/recall rate, F-score来选择这个ɛ值,而不能使用error rate,这是由于我们的样本集是数据倾斜的(skewed),即负样本数远大于正样本数,所以需要使用precision/recall rate, F-score, 如下图:
Anomaly Detection vs. Supervised Learning
本小节重点讲了在哪些情况下使用anomaly detection,哪些情况下使用supervised learning。其主要区别如下:
- 当y=1(即异常样本)的样本非常少的时候我们很难通过训练让supervised learning算法“学习”到什么时候为1;相比较而言如果有大量y=0的样本我们就可以计算其高斯分布情况,从而识别其为正常值的概率,通过阈值ɛ我们就可以知道何为异常,何为正常
- 当异常有很多种类的时候,甚至于有些异常可能之前都没有发生过,这种情况下很难通过supervised learning来“学习”到这种异常情况,所以这种情况更适合anomaly detection
Choosing Features
此小节主要讲了如何针对anomaly detection来选择feature。我个人的理解如下:
想象一下我们自己如何去识别这个异常,可以使用哪些“指标”来发现异常,那么这些“指标”就可以作为feature。
另外,在我们异常检测时,如果发现某个异常的样本在我们的模型中P值很高(即检测为正常),那么很有可能是其某个检测指标没有在我们的检测模型当中,我们可以看看这个异常值究竟哪里异常,用什么指标可以检测到这个异常,这样我们就可以为我们的异常检测系统发现新的feature,如下图所示:
另外, 我们还可以通过一些原始“指标”的组合来形成新的feature,如下图所示:
最后,我们需要看下我们这些feature的数值分布是否符合高斯分布,如果不符合,就需要将这些数据进行转换,让“新的feature”的数值分布符合高斯分布。如下图所示:
总结选择feature的过程如下:
- 根据我们人类经验,选择可能检测到异常的指标作为feature
- 通过CV和测试集发现模型中存在异常的样本但是P值却很高,分析可能遗漏的feature
- 还可通过原始指标的组合形成新的feature
- 将不符合高斯分布的指标进行转换
Multivariate Gaussian Distribution
本章主要讲了多元高斯分布模型(multivariate gaussian distribution)
multivariate gaussian distribution
在现实使用高斯分布的时候,我们会发现有些情况下两个feature是有相关性的,Andrew举了一个数据中心异常检测的例子,我们会发现计算机的cpu使用率和memory使用率是有一定相关性的,通常cpu使用率越高,memory使用率也就越高,如果一台机器CPU使用率很低,但是memory很高,那么异常的可能性就较大,这种情况下用我们之前的高斯分布模型就无法检测到,如下图所示:
- 图中可以看出虽然在同一个等高线上(红色圆圈)概率P是相同的,但是实际上在椭圆圈(蓝色椭圆)中的概率P显然应该更加高一些(由于cpu和memory的正相关)
- 这就是为什么我们需要引入多元高斯模型,从而可以让我们的高斯模型有更多调整和控制
多元高斯分布的计算公式如下图所示:
- 这里涉及到协方差矩阵和行列式的概念,具体可以参考wiki-协方差矩阵 和wiki - 行列式
- 行列式计算可以直接使用octave中的函数det来进行计算
接下来,我们看下协方差矩阵∑和均值μ是如何影响我们的分布模型的。
首先,协方差矩阵对角线上的数值会影响不同维度的高斯分布的宽度,如下图所示:
- 这里可以看到协方差矩阵对角线上的值会影响高斯分布的宽窄,而且对角线的第一个值(位置[1, 1])影响的是x1,其越大那么x1维度上高斯分布越宽,下降也越慢;对角线上第二个值([2,2])影响x2方向上的高斯分布。
再看第二个例子
- 这里看到另一个方向上的对角线的值影响的是x1, x2的相关性,值越大,x1和x2越相关
- 相关性的含义就是,当x1越大,正常情况下x2也越大(cpu和memory的例子), 这种情况下我们用这个模型就可以很好的契合本章刚开始的例子(高斯分布图已经变成了椭圆形)
也可以是负相关,即x1越大,相应的x2应当越小,可以通过设为负值让其负相关,如下图:
最后,均值会影响到高斯分布的中心点位置,如下图所示:
本节疑问是,中心点的概率应当是接近于1的,但是看到课程的示例其高点都没有到1,甚至远低于1,这个不明白为什么是这种情况?
Anomaly Detection Using Multivariate Gaussian Distribution
本小节主要讲如何使用多元高斯分布,首先我们要计算均值μ和协方差矩阵∑,如下图:
- 通过上图的公式计算好μ和∑之后,我们就可以将新的样本x一起代入公式当中,从而计算出概率P
实际上,原来的高斯模型是多元高斯模型的一个特殊形式而已,如下图所示:
这两种高斯模型各有利弊,反而original高斯模型使用更加频繁一些。其利弊比较如下图所示:
- 针对相关性问题,我们可以生成一个新的feature(如图x3),从而让original model也可以检测到这种相关性。相比较而言多元高斯模型是自动捕获这种相关性的。
- original模型计算相对简单,因此当n非常大的时候,就非常适合这i种模型。相较而言,多元高斯模型的计算量相当大。
- 最后由于数学上限制,当m
Recommendation System
Rating Movie
此小节主要讲了我们是如何在推荐系统中给电影进行预测打分的,重点是讲了一些notation,如下图:
Content Based Recommendations
此小节主要讲了如何基于内容进行推荐,本质上是将电影的一些特征组成一个特征向量,然后根据每个用户已经评分的电影样本进行训练(Linear Regression),从而为每一个用户都训练出一个单独的模型(即每个用户都会有一个不同的θ)这样的话,就可以针对没有评分的电影进行预测。过程如下图所示:
所以,我们的优化目标跟Linear Regression类似,只是我们需要针对每个用户都要计算其cost function的最小值,所以最终的公式如下图所示:
- 图4.3上边的公式是计算当个用户的优化目标,注意这里省略了m,因为不影响最后的θ值
-
图4.3下方的公式是针对所有用户的优化目标,实际就是把针对单个用户的优化目标相加
4.4-optimization algorithm - 根据我们的优化目标的公式,我们可以针对其进行梯度下降计算
- 注意这里是要针对每一个用户(θ(j))的每一个θk(k 从0到n)都要进行梯度计算。举个例子,假设我们的movie使用了两个特征值,那么我们的特征向量就是2+1个维度,所以我们要为每个用户都计算其相应的θ0,θ1,θ2。假设我们有5个用户需要计算(即j从1到5),那么总共要计算3x5=15个θ。
个人认为,实际项目中很难使用此种方法,因为大部分用户可能根本就不会去给电影评分,也就没有样本可以训练,因此也就无法训练出相应的模型
Collaborative Filtering
Collaborative Filtering
此章节重点讲协同过滤算法,为什么要使用协同过滤呢,主要原因在于如果电影数量庞大,我们手工去标注电影的feature x1, x2会非常麻烦,因此我们就会想,如果我们已知各个用户的θ值,是否也能推测出其feature值呢,如下图所示,显然是可以的:
然后,问题就转化为求如下最优解的问题:
- 这里的regularization item变成了针对x,而不是θ
- 当针对所有的movie的时候,我们要需要将x(1)到x(no of moview)的所有误差项都加总起来,如此就有了下方的公式。最终我们只需要针对下方的公式来求解最小值,从而得到x的最优解
那么,问题来了,我们又如何得到θ,从而去求解x呢?这成了一个先有鸡还是先有蛋的问题。解决此类问题的一种办法是,先随机取一组θ值,然后去优化x,用得到的x再去优化θ,循环往复,如下图所示:
下一节,我们会看到一种更好的办法。
Collaborative Filtering Algorithm
首先,我们可以将两组优化公式(一个是针对θ,另一个是针对x)整合在一起,如下图所示:
- 无论针对x还是针对θ,其本质都是找寻某个x和θ使得预测值(即某个用户针对某个电影的评分)和真实值(真实评分)之间的差值最小。而这个差值对于两个公式来说,本质是一样的,都是找寻有用户评分的电影( 即r(i, j)=1 ),和预测值,然后计算其差值的平方。
- 正则部分,由于我们是同时针对θ和x进行求解,因此就需要有同时针对θ和x的正则项。
- 另外,我们也不需要设定x0, θ0,这些都会交给算法自动训练出来。
最后,整个算法的训练和预测过程如下:
Low Rank Matrix Factorization
Vectorize: Low Rank Matrix Factorization
此小节主要是讲在计算预测值的时候,我们不需要一个用户一个电影的计算,而可以通过vectorization的方式进行计算,如下图所示:
由于这种计算方式在线性代数中叫做low rank matrix factorization,因此我们这种协同过滤算法有时也被称为low rank matrix factorization算法
随后Andrew又提出了一个问题,就是我们怎么样可以判断一个电影是相关的呢?针对一个电影,我们可能有很多的features,那么这时候如何判断两个电影的相关性呢?本质上我们可以用这些feature的vector来表示一部电影,这样电影就都可以用vector来表示了,那么问题就转化为如何判断两个vector的相关性了,通过前面的学习我们知道,其中一种方法就是看两个vector的欧几里得距离,具体如下图所示:
Implementation Detail: Mean Normalization
我们之所学所思皆来源于问题,那么此小节所讲正是来源于之前我提到的一个问题,即当用户评分很少或者干脆没有评分的时候怎么办?如下当用户没有任何评分的时候,最后我们通过优化公式优化的结果就是所有的θ均为0,那么预测值也就全是0,这样就没有预测效果了。
那么,我们该如何解决这个问题呢?一个最直观的办法就是将每部电影的平均评分赋给这个没有评分的用户。那么,我们不可能去找哪个用户没有评分,哪个用户评分数量不够,我们可以通过算法来解决这个问题,如下图所示:
- 通过mean normalization(即让原先的x,记作xori减去均值μ从而转化为新的features,记作xnew),我们可以得到一个新的feature matrix,然后再通过这个新的feature matrix来训练θ和xnew
- 最终预测的时候我们需要将均值加回来,因此就有(θ(j))T(x(i)new) + μ
- 针对没有评分的用户Eve,最终由于加了μ,所以其预测值就是均值。
其它疑问
- 视频中Andrew没有讲针对一个item,我们该如何选择其features?实际上,我们可能也无需关心某个feature的含义,但是feature的数量是需要我们去选择的。那么该如何解决呢?
答案是:做实验。比如我们可以先选择两个feature,训练之后,让其在CV集上预测,计算error rate,然后再选择5个feature尝试,再选择更多的feature尝试,最终我们可以绘制一个feature数量和error rate的关系图,从而判断feature数量n为几的时候,error rate最低。
- Andrew讲的协同过滤算法和网上搜索查到的协同过滤算法感觉并不是相同的算法,这是怎么回事?