- 什么是二叉树?
- 什么是二分搜索树?
- 二分搜索树的基本操作
- 二分搜索树添加新元素
- 二分搜索树的遍历(包含非递归实现)
- 删除二分搜索树中的元素
什么是二叉树?
在实现二分搜索树之前,我们先思考一下,为什么要有树这种数据结构呢?我们通过企业的组织机构、文件存储、数据库索引等这些常见的应用会发现,将数据使用树结构存储后,会出奇的高效,树结构本身是一种天然的组织结构。常见的树结构有:二分搜索树、平衡二叉树(常见的平衡二叉树有AVL和红黑树)、堆、并查集、线段树、Trie等。Trie又叫字典树或前缀树。
树和链表一样,都属于动态数据结构,由于二分搜索树是二叉树的一种,我们先来说说什么是二叉树。二叉树具有唯一的根节点,二叉树每个节点最多有两个孩子节点,二叉树的每个节点最多有一个父亲节点,二叉树具有天然递归结构,每个节点的左子数也是一棵二叉树,每个节点的右子树也是一颗二叉树。二叉树如下图:
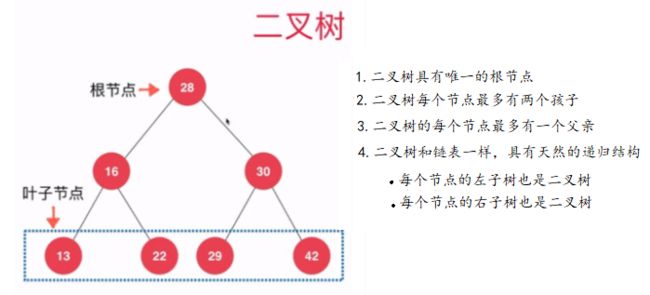
什么是二分搜索树?
二分搜索树也是一种二叉树,但二分搜索树种每个节点的值都要大于其左子树所有节点的值,小于其右子树所有节点的值,每一棵子树也是二分搜索树。正因为二分搜索树的这种性质,二分搜索树存储的元素必须具有可比较性。下图就是一棵二分搜索树:

我们可以根据二分搜索树的特点,构建一颗二分搜索树,代码实现如下:
/**
* 由于二分搜索树中的元素必须具有可比较性,所以二分搜索树中存储的数据必须要实现Comparable接口
* @param
*/
public class BST> {
//由于用户并不需要知道我们二分搜索树的具体实现,所以这里把节点设置成内部类
private class Node {
public E e;
public Node left, right;
public Node(E e) {
this.e = e;
left = null;
right = null;
}
}
//一棵树只有一个根节点
private Node root;
//节点的个数
private int size;
//无参构造,这里不写也可以,因为和系统默认的无参构造是相同的
public BST(){
root = null;
size = 0;
}
//获取节点的个数
public int size(){
return size;
}
//判断树是否为空
public boolean isEmpty(){
return size == 0;
}
}
二分搜索树的基本操作
二分搜索树添加新元素
我们在向二分搜索中添加元素时,需要保持二分搜索树的性质,即需要将我们添加的元素从根节点开始比较,若比根节点小,则去根节点的左子树递归进行添加操作,若比根节点的右子树递归进行添加操作,若相等,则直接返回,因为本文实现的是一棵不包含重复元素的二分搜索树。具体代码实现如下:
// 向二分搜索树中添加新的元素e
public void add(E e){
//判断根节点是否为空
if(root == null){
//如果根节点为空,则将新添加的元素作为根节点
root = new Node(e);
//节点的个数加一
size ++;
}
else
add(root, e);
}
// 向以node为根的二分搜索树中插入元素e,递归算法
private void add(Node node, E e){
//如果被添加的元素与当前节点的值相等,则直接返回 -- 本文的二分搜索中不包含重复元素
if(e.equals(node.e))
return;
//如果待添加元素e小于当前节点的值,并且当前节点没有左孩子
else if(e.compareTo(node.e) < 0 && node.left == null){
//则将待添加元素e作为当前节点的左孩子
node.left = new Node(e);
size ++;
return;
}
//如果待添加元素e大于当前节点的值,并且当前节点没有右孩子
else if(e.compareTo(node.e) > 0 && node.right == null){
//则将待添加元素e作为当前节点的右孩子,并返回
node.right = new Node(e);
size ++;
return;
}
//如果以上条件都不满足,则根据元素e和当前节点的值的比较,来确定去左子树递归进行添加操作,还是去右子树进行添加操作
if(e.compareTo(node.e) < 0)
add(node.left, e);
else //e.compareTo(node.e) > 0
add(node.right, e);
}
通过上面添加方法的代码实现中,可以看出有如下两点不足并且可以优化的地方:1.待添加元素e需要与当前节点的值进行两轮比较;2.递归终止条件太臃肿了.我们可以来简化一下上面的添加元素的方法,如下:
// 向二分搜索树中添加新元素e
public void add(E e){
root = add(root,e);
}
//向以node为根的二分搜索树中插入元素e,递归算法
private Node add(Node node, E e) {
if (node == null){
node = new Node(e);
size ++;
return node;
}
if (e.compareTo(node.e) < 0){
node.left = add(node.left,e);
}else if (e.compareTo(node.e) > 0){
node.right = add(node.right , e);
}
return node;
}
改进之后添加方法就简洁很多了,现在我们完成了二分搜索树的添加后,想一下如何在二分搜索中查找某个元素呢?我们可以用contains()方法来表示当前二分搜索中是否包含该元素,代码实现如下:
//看二分搜索树中是否包含元素e
public boolean contains(E e){
//使用递归查找
return contains(root,e);
}
private boolean contains(Node node, E e) {
//如果根节点为空,则该二分搜索中肯定没有带查找元素e,直接返回false
if (node == null)
return false;
//如果当前节点的值和待查找元素e相等,则返回true
if (e.compareTo(node.e) == 0){
return true;
//如果待查找元素e小于当前节点的值,则去当前节点的左子树进行递归查找
}else if (e.compareTo(node.e) < 0 ){
return contains(node.left,e);
//如果待查找元素e大于当前节点的值,则去当前节点的右子树进行递归查找
}else { //(e.compareTo(node.e) > 0 )
return contains(node.right,e);
}
}
二分搜索树的遍历(包含非递归实现)
什么是遍历操作?
遍历操作就是把所有的节点都访问一遍,当然访问的原因和你如何访问都和你具体的业务相关,本文主要是通过在在控制台打印输出该节点的值,来完成访问的。我们知道在线性结构下,遍历是极其容易的,比如数组和链表的遍历,当然在树结构下,我们可以通过递归来使二分搜索树的遍历变得非常简单。
- 递归实现
1. 前序遍历
//二分搜索树的前序遍历 -- 递归算法
public void preOrder(){
preOrder(root);
}
private void preOrder(Node node) {
if (node == null)
return;
//访问该节点
System.out.print(node.e +"\t");
//递归遍历左子树
preOrder(node.left);
//递归遍历右子树
preOrder(node.right);
}
就几行代码,我们就已经完成了我们的前序遍历,是不是很简单,我们现在可以来测试一下我们前面写的添加方法和现在的前序遍历操作,为了更好在控制台看我们的打印结果,我们需要重写一下二分搜索树的toString(),我们可以用“--”来表示节点所在的深度,让输出效果更直观,实现如下:
//重写toString()
@Override
public String toString() {
StringBuilder builder = new StringBuilder();
generateBSTString(root,0,builder);
return builder.toString();
}
//生成以node为根节点,深度为depth的描述二叉树的字符串
private void generateBSTString(Node node, int depth, StringBuilder builder) {
if(node == null){
builder.append(generateDepthString(depth) + "null\n");
return;
}
builder.append(generateDepthString(depth) + node.e + "\n");
generateBSTString(node.left,depth+1,builder);
generateBSTString(node.right,depth+1,builder);
}
//添加深度标识符
private String generateDepthString(int depth) {
StringBuilder res = new StringBuilder();
for (int i=0; i我们可以在主方法中添加我们的测试代码,测试代码如下:
public static void main(String[] args) {
BST bst = new BST();
int[] nums = {5, 3, 6, 8, 4, 2};
for(int num: nums){
//二分搜索树的添加操作
bst.add(num);
}
//前序遍历 -- 递归算法
bst.preOrder();
System.out.println();
System.out.println(bst);
}
我们现在根据上面的测试代码,来一起看下运行结果:
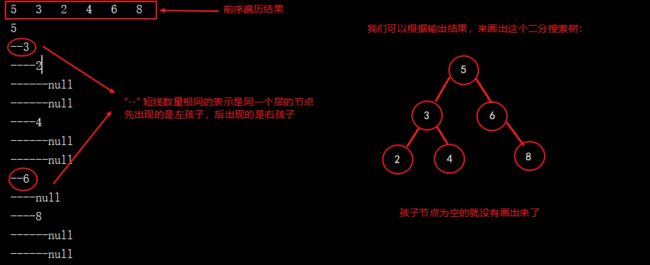
我们根据运行结果画出的树结构,可以看出是满足二分搜索树的性质的,因此也证明了我们的添加方法和前序遍历是没有问题的。
2. 中序遍历
根据我们的前序遍历的递归实现,我们可以很容易地写出二分搜索树的中序遍历,具体实现如下:
//二分搜索树的中序遍历 -- 递归算法
public void inOrder(){
inOrder(root);
}
private void inOrder(Node node) {
if (node == null)
return;
//遍历左子树
inOrder(node.left);
//通过打印输出该节点的值的形式,访问该节点
System.out.print(node.e + "\t");
//遍历右子树
inOrder(node.right);
}
3. 后序遍历
通过前序遍历和中序遍历的学习,我相信大家对后序遍历的递归实现已经觉得非常容易了,代码如下:
//二分搜索树的后序遍历 --递归算法
public void postOrder(){
postOrder(root);
}
private void postOrder(Node node) {
if ( node== null )
return;
//遍历左子树
postOrder(node.left);
//遍历右子树
postOrder(node.right);
//通过打印输出该节点的值的形式,访问该节点
System.out.print(node.e+"\t");
}
- 非递归实现
1. 前序遍历
实现思路:当我们使用非递归来实现二分搜索树的前序遍历时,我们可以借助栈这种数据结构,由于栈是后进先出的,我们需要先将当前节点的右孩子压入栈中,再将当前节点的左孩子压入栈中,当我们的栈不为空时,我们就循环执行出栈操作,并且将出栈的元素作为当前节点。当然,如果你还不了解栈这种数据结构,你可以看我的上篇文章:常见的线性结构进行学习。非递归前序遍历具体代码实现如下:
//前序遍历 -- 非递归实现
public List preOrderTraversal(TreeNode root) {
//该集合用来保存通过前序遍历后的元素
List res = new ArrayList();
if (root == null)
return res;
//借助栈这种数据结构进行实现
Stack> stack = new Stack>();
//由于前序遍历的一个元素一定是根节点,所以我们可以先将根节点压入栈中
stack.push(root);
//判断栈是否为空
while ( !stack.isEmpty() ){
//将出栈的节点保存起来
TreeNode curr = stack.pop();
//将出栈节点的值添加到集合中
res.add(curr.val);
//若当前节点的右孩子不为空,就将该节点的右孩子压入栈中
if (curr.right != null)
stack.push(curr.right);
//若当前节点的左孩子不为空,就将该节点的左孩子压入栈中
if (curr.left != null)
stack.push(curr.left);
}
return res;
}
2. 中序遍历
二分搜索树中序遍历的非递归实现,这里还是通过借助栈来实现的,理解起来要比前序遍历的非递归实现复杂一些,希望大家可以认真思考,仔细体会,具体代码实现如下:
//中序遍历 -- 非递归实现
public List inOrderTraversal(TreeNode root){
List res = new ArrayList();
if (root == null)
return res;
TreeNode cur = root;
Stack stack = new Stack();
while (cur != null || !stack.isEmpty()){
if (cur != null) {
stack.push(cur);
cur = cur.left;
}else {
cur = stack.pop();
res.add(cur.val);
cur = cur.right;
}
}
return res;
}
3. 后序遍历
我们通过前面的前序遍历和中序遍历的非递归算法的实现,都是采用的栈这种数据结构进行实现,这也和我们程序调用的系统栈的工作原理相似,下面我们后序遍历的非递归算法仍然接站栈这种数据结构进行实现,这样可以帮助我们更加的熟悉栈这种数据结构的应用,具体代码实现如下:
//后序遍历 -- 非递归算法
public List postOrderTraversal(TreeNode root) {
List res = new ArrayList();
if (root == null)
return res;
//借助栈结构实现二分搜索树的非递归后序遍历
Stack stack = new Stack();
TreeNode curr = root;
TreeNode pre = null;
while (curr != null || !stack.isEmpty()) {
if (curr != null){
stack.push(curr);
curr = curr.left;
}else {
curr = stack.pop();
if (curr.right == null || curr.right == pre){
res.add(curr.val);
pre = curr;
curr = null;
}else {
stack.push(curr);
curr = curr.right;
}
}
}
return res;
}
4. 层序遍历
层序遍历和前面三种遍历方式都不一样,前、中、后序遍历本质上都是深度优先遍历,在进行前、中、后序遍历时,会先一直走到二分搜索树的叶子节点,也就是最大深度,而我们的层序遍历,本质上是一种广度优先遍历,就是横向遍历完所有节点后,再遍历下一层节点,如下图:
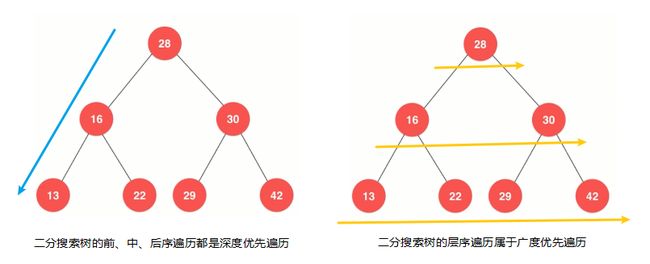
那么二分搜索树的层序遍历如何实现呢,我们前面讲过队列这种数据结构是先进先出的,我们可以将二分搜索树中的每层节点顺序放进队列中,然后再进行出队操作就可以了,若你不清楚队列,你可以看我的上篇文章常见的线性结构进行学习,现在就让我们来看是如何使用队列实现二分搜索树的层序遍历吧,具体代码实现如下:
//层序遍历
public void levelOrder(){
if (root == null)
return;
Queue queue = new LinkedList();
queue.add(root);
while ( !queue.isEmpty()){
Node removeNode = queue.remove();
System.out.print(removeNode.e+"\t");
if (removeNode.left != null)
queue.add(removeNode.left);
if (removeNode.right != null)
queue.add(removeNode.right);
}
}
删除二分搜索树中的元素
由于删除二分搜索中的任意元素是比较复杂的,我们可以先研究如何实现删除二分搜索树的最大值和最小值,当然我们得先找到这棵二分搜索树的最大值和最小值,查找方法如下:
//寻找二分搜索树中最大元素 -- 递归获取
public E maxNum(){
if (size == 0)
throw new IllegalArgumentException("BST is empty");
//递归调用获取二分搜索中最大值所在的节点的方法
Node maxNode = maxNum(root);
return maxNode.e;
}
//以node为根节点,获取二分搜索中最大值所在的节点
private Node maxNum(Node node) {
//递归终止条件---如果当前节点的右孩子为空,则返回当前节点
if (node.right == null)
return node;
//递归从当前节点的右子树获取最大值所在的节点
return maxNum(node.right);
}
//寻找二分搜索数中的最小元素 -- 递归法
public E minNum(){
if (size == 0) // 也可以写为 root==null
throw new IllegalArgumentException("BST is empty");
Node minNode = minNum(root);
return minNode.e;
}
//以node为根节点搜索最小元素所在的节点
private Node minNum(Node node) {
if (node.left == null)
return node;
//递归从当前节点的左子树获取最小值所在的节点
return minNum(node.left);
}
现在我们已经找出最小元素和最大元素所在的节点了,我们现在就可以是实现删除最小元素和最大元素所在的节点操作了,代码如下:
//从二分搜索树中删除最小元素所在的节点,并返回最小元素的值
public E removeMinNum(){
//获取最小值
E e = minNum();
root = removeMinNum(root);
return e;
}
//以node为根节点删除最小元素所在的节点
private Node removeMinNum(Node node) {
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
node.left = removeMinNum(node.left);
return node;
}
//删除二分搜索数中最大元素所在的节点,并返回该值
public E removeMaxNum(){
//获取最大值
E e = maxNum();
root = removeMaxNum(root);
return e;
}
//删除以node为根节点的二分搜索中最大元素所在的节点
private Node removeMaxNum(Node node) {
if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
node.right = removeMaxNum(node.right);
return node;
}
在我们实现删除二分搜索树中的最大元素所在的节点和删除最小元素所在的节点操作后,我们可以写一个简单的测试用例,来验证下我们的删除最大值和删除最小值操作是否正确:
public static void main(String[] args) {
BST bst = new BST();
Random random = new Random();
int n = 1000;
// 测试删除最小元素所在的节点
for(int i = 0 ; i < n ; i ++)
bst.add(random.nextInt(10000));
List nums = new ArrayList();
while(!bst.isEmpty()){
//从二分搜索树中删除最小元素所在的节点,并拿到该最小元素
Integer minNum = bst.removeMinNum();
//向我们的集合中添加该最小元素
nums.add(minNum);
}
//我们的nums集合中存储的是二分搜索树中所有节点的值按从小到大顺序排序后的元素
System.out.println(nums);
for(int i = 1 ; i < nums.size() ; i ++)
//如果该集合中前一个元素的值大于后一个元素的值,则不满足从小到大的排序规则,则抛出错异常
if(nums.get(i - 1) > nums.get(i))
throw new IllegalArgumentException("Error!");
System.out.println("removeMin test completed.");
// 测试删除最大元素所在的节点
for(int i = 0 ; i < n ; i ++)
bst.add(random.nextInt(10000));
nums = new ArrayList();
while(!bst.isEmpty()){
//从二分搜索树中删除最大元素所在的节点,并拿到该最大元素
Integer maxNum = bst.removeMaxNum();
//向我们的集合中添加该最小元素
nums.add(maxNum);
}
//我们的nums集合中存储的是二分搜索树中所有节点的值按从大到小倒序排序后的元素
System.out.println(nums);
for(int i = 1 ; i < nums.size() ; i ++)
//如果该集合中前一个元素的值小于后一个元素的值,则不满足从大到小的排序规则,则抛出错异常
if(nums.get(i - 1) < nums.get(i))
throw new IllegalArgumentException("Error!");
System.out.println("removeMax test completed.");
}
有了如上操作作为铺垫后,现在就可以来实现删除二分搜索树中的指定元素的操作了,需要注意的是,当待删除节点的左右子树都不为空时,我们需要找到待删除元素的后继或者前驱,后继就是指待删除节点右子树中最小的元素所在的节点,前驱是指待删除节点左子树最大的元素所在的节点。本文是采用的待删除节点的后继来代替待删除元素的位置。
前驱图示:待删除节点右子树中最小的元素所在的节点
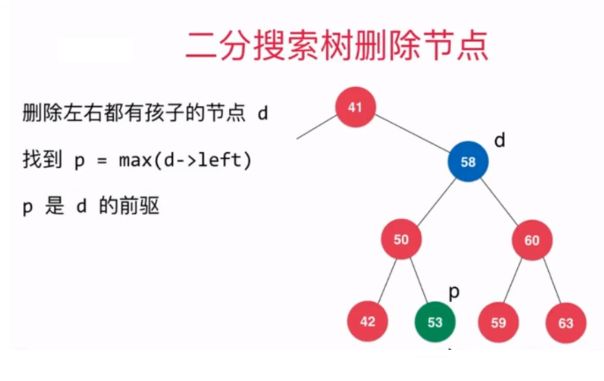
后继图示:待删除节点左子树最大的元素所在的节点
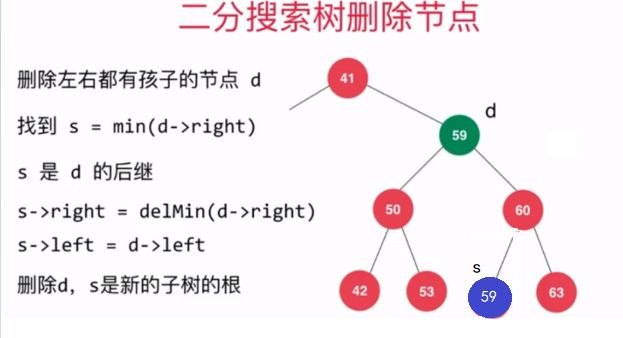
具体代码实现如下:
//删除二分搜索树中的指定元素
public void removeElement(E e){
root = removeElement(root,e);
}
// 删除掉以node为根的二分搜索树中值为e的节点, 递归算法
// 返回删除节点后新的二分搜索树的根
private Node removeElement(Node node, E e) {
if (node == null)
return null;
if (e.compareTo(node.e) <0 ){
node.left = removeElement(node.left, e);
return node;
}else if (e.compareTo(node.e) >0 ){
node.right = removeElement(node.right,e);
return node;
}else { //e.compareTo(node.e) == 0
//待删除节点左子树为空的情况
if (node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
//待删除节点的右子树为空的情况
if (node.right == null){
Node leftNode = node.left;
node.left = null;
size -- ;
return leftNode;
}
//待删除节点的左右子树都不为空的情况
// 待删除节点的后继:找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minNum(node.right);
successor.right = removeMinNum(node.right);
successor.left = node.left;
node.right = node.left = null;
return successor;
}
}
本文实现的是一个不包含重复元素的二分搜索树,若你需要你的二分搜索树包含重复元素,在进行添加操作时只需要定义左子树小于等于节点;或者右子树大于等于节点。二分搜索树的学习就到这里了,希望本文能让你对二分搜索树有更深的理解。