声明:本笔记所涉及的资料来源于牛客网
认识时间复杂度
常数时间的操作:一个操作如果和数据量没有关系,每次都是固定时间内完成的操作,叫做常数操作。我的理解是这种操作最终的执行就是执行汇编命令,而汇编命令执行花费的时间都是有限的机器时钟时间,可以简单理解为执行一个相加指令,所以常数操作花费的时间是确定有限的,和数量级没关系。
时间复杂度为一个算法流程中,常数操作数量的指标,常用O(读作 big O)来表示。具体来说,在常数操作数量的表达式中,只要有高阶项,不要低阶项,也不要高阶项的系数,剩下的部分如果记为f(N),那么时间复杂度为O(f(N))。
评价一个算法流程的好坏,先看时间复杂度的指标,然后再分析不同数据样本下的实际运行时间,也就是常数项时间。
一个简单理解时间复杂度的例子:
一个有序数组A,另一个无序数组B,请打印B中的所有不在A中的数,A数组长度为N,B数组长度为M。
- 算法一:对于B数组的每一个数,都在A中通过遍历的方式找一下
这相当于两个for循环,所以常数操作量f(M,N) = M * N ,所以算法复杂度为O(M * N)
- 算法二:对于B数组的每一个数,都在A中通过二分查找的的方式找一下
二分查找常数操作量约为Log2N,所以总的算法复杂度为O(M * logN),log下标可省,一般看做2
- 算法三:先把数组B排序,然后用类似外排的方式打印所有在A中出现的数
排序时间复杂度可为O(M * logM),外排打印时间复杂度为O(M + N),所有总的时间复杂度为O(M * logM) + O(M + N)
所以具体算法的优劣还要看实际的数量级,算法二肯定比算法一要优,算法二和算法三需要考虑M,N的取值范围来判断
对数器的概念和使用
如果你有个想要测的方法a,你可以实现一个绝对正确但是复杂度不好的方法b,然后实现一个随机样本产生器,还要实现一个对比的方法,这样方法a和方法b比对多次来验证方法a是否正确。而且如果有一个样本使得对比出错,可以打印样本分析是哪个方法错误。当样本数量很多时比对测试依然正确,可以确定方法a已经正确。
冒泡排序复杂度分析
第一次冒:0 ............. n-1
第二次冒:0 ....... n-2
第三次冒:0 ... n-3
直到冒完
所有伪代码可以这样:
public static void bubbleSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int e = arr.length - 1; e > 0; e--) {
for (int i = 0; i < e; i++) {
if (arr[i] > arr[i + 1]) {
swap(arr, i, i + 1);
}
}
}
}
可知当数量级为N时,常数操作量就是N*N,时间复杂度就为O(N^2),空间复杂度因为只是操作原数组,没有声请什么额外的空间,所以为常数,额外空间复杂度为O(1)
选择排序的复杂度分析
第一次从0 .................n-1中选择出最小(大)值放在0
第二次从 1 .................n-1中选择出最小(大)值放在1
第三次从 2 .................n-1中选择出最小(大)值放在2
知道选择完
伪代码:
public static void selectionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int e = 0; e < arr.length-1; e ++) {// 最后一个不用比
int min = e;
int i = e + 1;
while( i < arr.length ){
min = arr[min] < arr[i] ? i : min;
i++;
}
swap(arr,e,min);
}
}
同理:时间复杂度O(N^2),额外空间复杂度O(1)
递归行为和递归行为时间复杂度的计算
递归的实现实质是方法数据的栈的压入和弹出,压入或弹出的数据即为方法的一些属性数据,如方法指针,参数,结果等
最典型的应用就是归并排序
套路就是:最外面一层把主问题分为两个小问题,加一个merge处理块
套路公式:
master公式:T(N) = a * T (N / b) + O(N ^ d)
- log(b,a) > d -> 复杂度为O(N^log(b,a))
- log(b,a) = d -> 复杂度为O(N^d * logN)
- log(b,a) < d -> 复杂度为O(N^d)
a 为子规模执行次数,b 为主规模分了几个子规模,d 为merge处理的负责度里的N的系数
例:归并排序
public static void mergeSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
mergeSort(arr, 0, arr.length - 1);
}
public static void mergeSort(int[] arr, int l, int r) {
if (l == r) {
return;
}
int mid = l + ((r - l) >> 1);
mergeSort(arr, l, mid);
mergeSort(arr, mid + 1, r);
merge(arr, l, mid, r);
}
public static void merge(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
int p1 = l;
int p2 = m + 1;
while (p1 <= m && p2 <= r) {
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= m) {
help[i++] = arr[p1++];
}
while (p2 <= r) {
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[l + i] = help[i];
}
}
最外层将主规模分为了2个子规模f(n/2)执行,所以a = 2,b = 2,merge处理复杂度为O(2N) = O(N) ,所以d = 1,所以T(N) = 2(N/2) + O(N)
所以log(b,a) = d = 1 ,时间复杂度为O(N * logN)
额外空间复杂度为O(N),主要是每次merge都申请了新的数组空间
应用 小和问题
public static void main(String[] args){
int[] arr = Util.generateRandomArray(8,10);
smallSum(arr);
}
public static void smallSum(int[] arr){
if (arr == null || arr.length < 2) {
return;
}
System.out.println("原数组");
Util.printArray(arr);
System.out.println("");
int smallSum = deal(arr,0,arr.length-1);
System.out.println("处理后的数组:");
Util.printArray(arr);
System.out.println("小和为:"+smallSum);
}
public static int deal(int[] arr,int left,int right){
if (left == right){
return 0;
}
int middle = left + ((right-left)>>1);
return deal(arr,left,middle) + deal(arr,middle+1,right)+merge(arr,left,middle,right);
}
public static int merge(int[] arr,int left,int middle,int right){
int[] help = new int[right-left+1];
int sum = 0;
int index = 0;
int p1=left;
int p2=middle+1;
while (p1 <= middle && p2 <= right){
if (arr[p1] < arr[p2]){
System.out.println((right-p2+1)+"个"+arr[p1]+" \n");//打印加数
}
sum += arr[p1] < arr[p2]? (right-p2+1)*arr[p1]:0;
help[index++] = arr[p1] < arr[p2]? arr[p1++] : arr[p2++];
}
while (p1 <= middle){
help[index++] = arr[p1++];
}
while (p2 <= right){
help[index++] = arr[p2++];
}
for (int i = 0;i < help.length;i++){
arr[left+i] = help[i];
}
return sum;
}
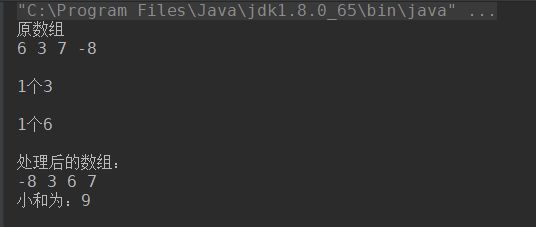
随机测试结果:
逆序对问题
在一个数组中,左边的数如果比右边的数大,则折两个数构成一个逆序对,请打印所有逆序对。
public static void main(String[] args){
int[] arr = Util.generateRandomArray(8,10);
System.out.println("原始数组:"+Arrays.toString(arr));
nixudui(arr);
System.out.print("处理后数组:"+Arrays.toString(arr));
}
public static void nixudui(int[] arr){
deal(arr,0,arr.length-1);
}
public static void deal(int[] arr,int left,int right){
if (left == right){
return;
}
int middle = left + ((right-left)>>1);
deal(arr,left,middle);
deal(arr,middle+1,right);
merge(arr,left,middle,right);
}
public static void merge(int[] arr, int left,int middle, int right){
int p1=left;
int p2 = middle+1;
int i = 0;
int[] help = new int[right-left+1];
while (p1 <= middle && p2 <= right){
if (arr[p1] > arr[p2]){
for(int j = 0;j < middle-p1+1;j++){
System.out.println("逆序对:"+arr[p1+j]+" "+arr[p2]);
}
help[i++] = arr[p2++];
}else {
help[i++] = arr[p1++];
}
}
while (p1 <= middle){
help[i++] = arr[p1++];
}
while (p2 <= right){
help[i++] = arr[p2++];
}
for ( i = 0;i < help.length;i++){
arr[left+i] = help[i];
}
}
执行结果:
和小和问题是同样的套路,时间复杂度为O(N * log N),空间复杂度为O(N)
拓展
二分查找的时间复杂度
二分查找的基本思想是将n个元素分成大致相等的两部分,取a[n/2]与x做比较,如果x=a[n/2],则找到x,算法中止;如果x
时间复杂度无非就是while循环的次数!
总共有n个元素,
渐渐跟下去就是n,n/2,n/4,....n/2^k(接下来操作元素的剩余个数),其中k就是循环的次数
由于你n/2^k取整后>=1
即令n/2^k=1
可得k=log2n,(是以2为底,n的对数)
所以时间复杂度可以表示O(h)=O(log2n)