本文始发于个人公众号:TechFlow,原创不易,求个关注
今天是LeetCode系列第22篇文章,今天讲的内容是高精度算法。
今天和大家讨论的算法是高精度,对应的LeetCode是第43题。题面其实没什么好说的,以字符串的形式给定两个数字,要求返回这两个数字的乘积。之所以是以字符串的形式给数字是因为这个数字可能会非常大,题目当中给定的范围是110位的数字。对于Python来说这不是问题,但是对于C++和Java等语言来说这么大的数字是无法以int类型存储的,所以必须要使用字符串来接收。
如果你使用Python,你可以不用任何算法就AC这题,但是这没有任何意义。那么正确的方法应该怎么做呢?
高精度与打竖式
这就需要我们的高精度算法出场了,其实严格说起来高精度并不是一种算法,而是一种思想。这个思想非常朴素,我敢保证我们每一个人都学过。还记得小学的时候,我们计算多位数的乘法是怎么算的吗?大家应该都不陌生才对,就是打竖式,like this:
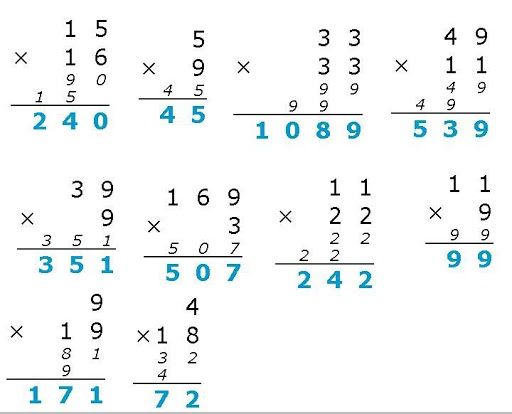
我们人类要打竖式是因为我们只能计算一位数以内的加减乘除,超过一位的人脑不能直接计算,我们就需要用纸笔记录下来进行计算。
纸笔计算的方法很简单,就是一位一位地计算,用每一位数字依次去计算乘法,最后再移位相加起来就得到结果了。
比如在上图的第一个例子当中,我们要计算15 * 16,我们先计算6 * 15的结果,再计算1 * 15,最后将两个结果错位相加,就得到了答案。我们要错位的原因也很简单,因为我们在计算15 * 1的时候,其实背后代表的是15 * 10。我们继续拆分问题,当我们计算6和15相乘的时候,又是怎么计算的呢?顺着这个思路,整个过程可以进一步被划分成先计算6和5相乘,再计算6和1相乘。
最后,我们把两个较大数字的相乘拆分成了在每一位上的数字相乘。到了这里,剩下的就简单了,也就是说我们可以把这两个很大的数字用两个数组来存储,数组当中的每一位存储数字上的一位。
比如我们要计算123 * 224, 我们的第一个数组是[1, 2, 3],我们的第二个数组是[2, 2, 4]。我们仿照乘法竖式中的方法计算这两个数组当中两两的乘积,并将它们拼装成答案。
1 2 3
* 2 2 4
____________
4 9 2
2 4 6
2 4 6
____________
2 7 5 5 2
同样我们用数组来存储中间和最后的结果,最后的结果就是:[2, 7, 5, 5, 2]。由于题目需要我们要返回的是字符串,所以我们还需要将数组里的内容再拼接成字符串。
这种用数组来模拟数字进行加减乘除运算的方法就叫做高精度算法,相信大家也都看到了,严格说起来这并不是一个算法,而只是一种思想。今天的题目出的是乘法,我们利用同样的方法也可以计算加减和除法。其中加减法非常简单,而除法则要复杂得多,也是高精度当中最难实现的部分。这里我们不做过多的拓展,计算的方法同样是打竖式,感兴趣的同学可以自行实现。
进位和前导零
当我们理清楚了打竖式的方法之后,我们还要面临进位和前导零的问题。
进位应该很容易理解,我们需要在计算乘法的时候判断当前位置的元素是否大于等于10,如果超过10的话,我们则需要进行进位。我们只需要将它除以10,得到的结果就是我们需要进位的值。除此之外就是前导零的问题,我们都知道除了零以外的合法数字是不允许首位出现0的,但是由于我们计算的是乘法,所以当其中某一个数为0会得到整体的结果为0,但是表示在数组当中则是多个0.
举个简单的例子,比如123 * 0,最后得到的应该是0,但是由于我们用数组表示了乘法运算当中的每一位,并且还进行了加法计算,所以会导致出现000的结果。这种情况我们要做特殊的处理,不过这也不复杂。最后我们把上面所有的思路都整理一下,就可以得到结果了。
我们来看下代码:
class Solution:
def multiply(self, num1: str, num2: str) -> str:
# 将字符串转化成数组
# 翻转数组,因为我们用第0位表示个位
arr1 = [ord(i) - ord('0') for i in num1][:: -1]
arr2 = [ord(i) - ord('0') for i in num2][:: -1]
# 创建结果数组,可以证明结果的长度最多是n + m
n, m = len(arr1), len(arr2)
ret = [0 for i in range(n + m + 1)]
for i in range(n):
for j in range(m):
# 按位相乘,计算进位
ret[i + j] += arr1[i] * arr2[j]
if ret[i+j] >= 10:
ret[i+j+1] += ret[i+j] // 10
ret[i+j] %= 10
# 最后把数组再转化成字符串返回
# 去除前导零
result = ''.join(map(str, ret))[::-1].lstrip('0')
return result if len(result) > 0 else '0'
今天的题只是Medium难度,并不算困难,会选这题的原因主要是为了高精度算法。高精度算法本身并不难,也并不常用即使是在算法比赛当中也不常见。但是它给了我们一个思路,当我们要计算的数值超过计算机目前承载能力的时候,我们还有什么方法?
当然这题我们也可以取巧,因为Python当中内置了大整数,当它检测到我们的计算结果超过范围的时候,会自动转化成大整数来进行计算。所以这题如果我们使用Python,可以只用几行代码搞定:
class Solution:
def multiply(self, num1: str, num2: str) -> str:
num1 = int(num1)
num2 = int(num2)
return str(num1 * num2)
今天关于高精度算法的内容就到这里,如果觉得有所收获,请顺手点个关注或者转发吧,你们的举手之劳对我来说很重要。
