说起红黑树就头痛,在大学时就没搞懂,看的晕晕乎乎,理解不了。直到前几天在极客时间的《数据结构与算法之美》专栏中的《26 | 红黑树(下):掌握这些技巧,你也可以实现一个红黑树
》,再次看到讲解红黑树插入删除如何保持平衡,很可惜,还是没看明白。但在留言区看到小伙伴推荐的红黑树是2-3树的变形,以2-3树的角度去理解红黑树就容易多了。于是,就跑去看了2-3树相关的文章,发现理解起来是要简单些。
2-3树定义
一般我们接触最多的是二叉树,也就是一个父节点最多有两个子节点。2-3树的意思就是说,一个父节点可以有两个子节点,也可以有三个子节点,并且其也满足类似二叉搜索树的定义(父节点的值大于左子树,但小于右子树),所有叶子节点都在同一层。
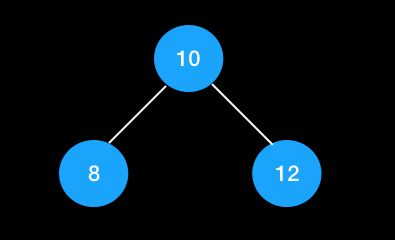
2节点:父节点存储一个值,最多有左右两个子树。假设父节点为p,子节点为l(左节点)、r(有节点),且满足:
l < p < r
如图所示:
3节点:父节点存储两个值,最多有左中右三个子树。假设父节点分别为p1,p2,子节点分别为l(左节点)、m(中间节点)、r(右节点),且满足:
l < p1
p1 < m < p2
r > p2
如图所示:
2-3树的查找
跟BST的查找类似:
从根节点开始比较,若相等,则结束。如果小于根节点,则说明它应该在左边,选定左节点进行比较;如果大于根节点,则说明在右边,选定右节点进行比较,如不相等,则继续循环。如到最后访问到空节点,则说明没找到。
只不过对于3节点的情况,就需要判断左中右子树,原理一样。
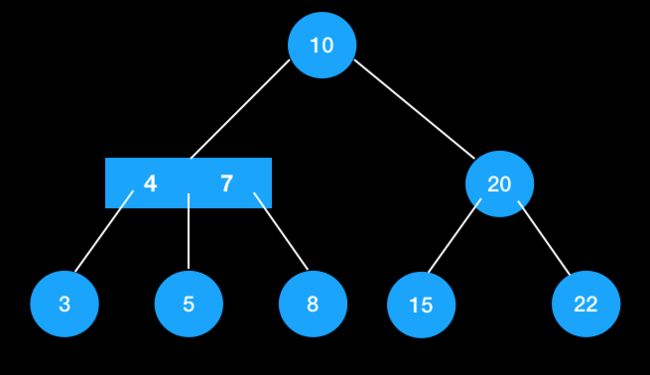
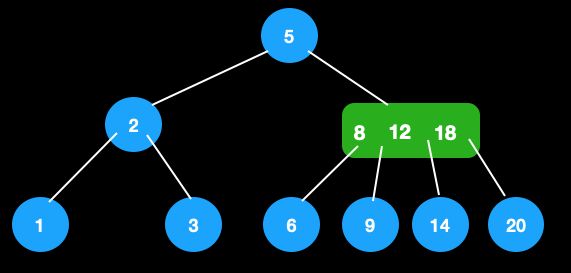
下面以这颗树举例说明,要查找的值存在和不存在的情况。
值存在
查找5。
- 对比根节点10。由于5<10,查找左子树。
- 由于4<5<7,所以需要找中间的子树。
- 节点值=5,查找结束。
值不存在
查找24。
- 对比根节点。由于24>10,查找右子树。
- 24>20,继续查找右子树。
- 24>22,查找右子树。
- 节点为空,查找结束,未找到。
节点分裂与合并
在将插入之前,先介绍一下节点分裂与合并。
2-3树只能存在2节点和3节点,由于插入的时候会引入4节点,所以我们需要将其分裂。
节点分裂
比如单个4节点,只需将中间节点往上提,左边值作为其左子树,右边值作为其右子树即可。
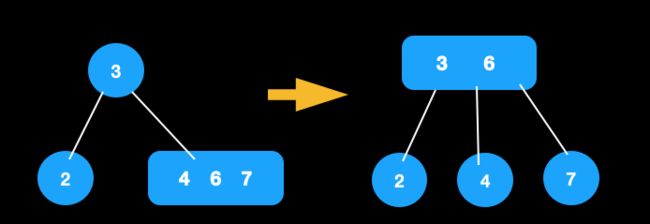
节点合并
比如有父节点的4节点,节点分裂后,需与父节点进行合并。若合并后父节点还是4节点,则继续分裂,直至满足定义为止。下图中6与3合并后,满足条件,无需再进行操作。
2-3树的插入
插入一个节点后,也要满足2-3树的定义。我们需要找到一个适合的位置来插入新的值,但是和二叉树不同的是,它不会生成新的叶子节点来存储,而是找到合适的叶子节点来进行合并。
但是注意,插入的原则是尽量保持树的高度,也就是尽量不要增加树的高度。因为树的高度越小,查找效率会更高。
下面分几种情况来说明不同的处理情况。其关键字是往上分裂,从下往上生长。
空树
生成新节点,则其为根节点。
待插入节点为2节点
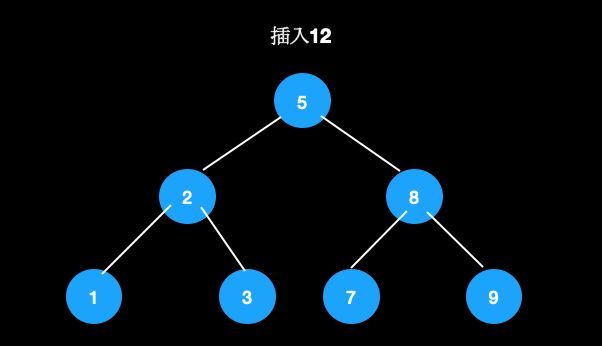
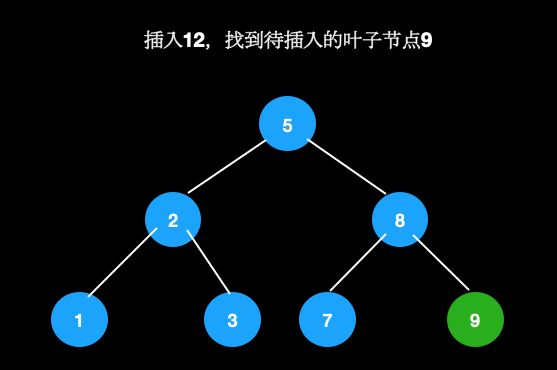
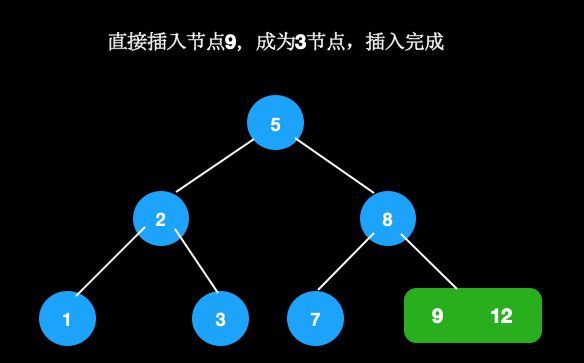
如果不能直接放到空的子节点,则放到父节点中,此时成为3节点,仍然满足定义。比如我们在这棵树中插入12。
-
首先找到待插入节点9。
- 节点9为2节点,可直接插入。
待插入节点为3节点
这种情况下,稍微会复杂一些,因为涉及到分裂,且跟待插入节点的父节点有关。假定待插入节点为p,待插入节点的父节点为pp。
将节点强插到p中,此时p中会有三个值,我们暂且称之为4节点。4节点是不满足2-3树的定义的,因此需要将4节点中的某个节点往上抽离,与pp进行合并。这时需要考虑pp的类型了。
-
若
pp为二节点将分裂的节点放到
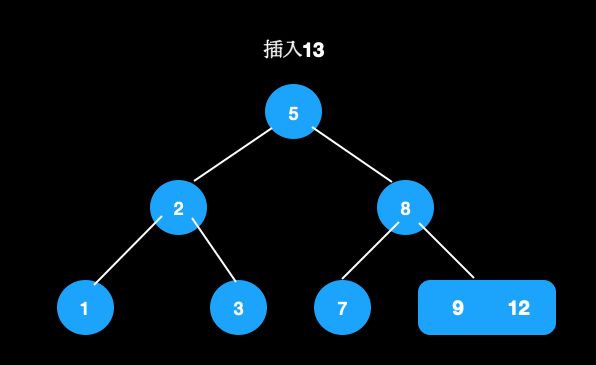
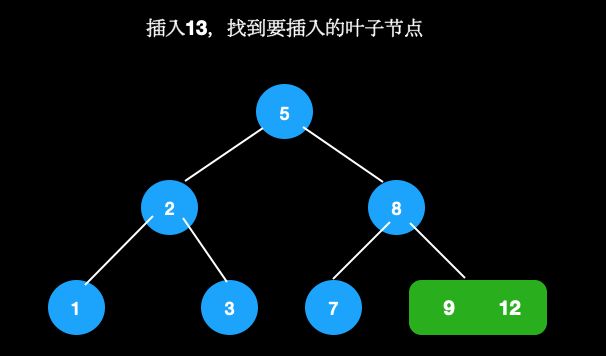
pp中,则pp成为3节点,满足定义。比如我们在这棵树中插入13。
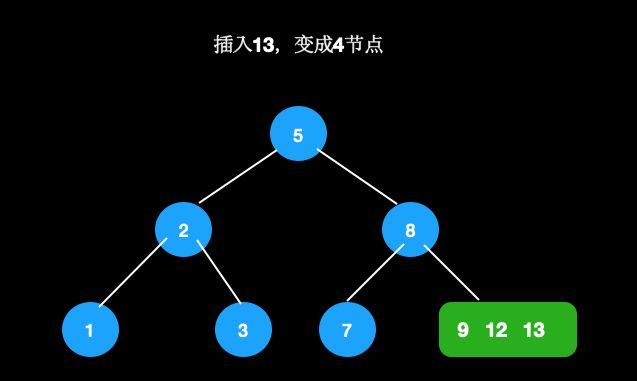
- 找到待插入叶子节点[9,12]
- 插入13,变成4节点
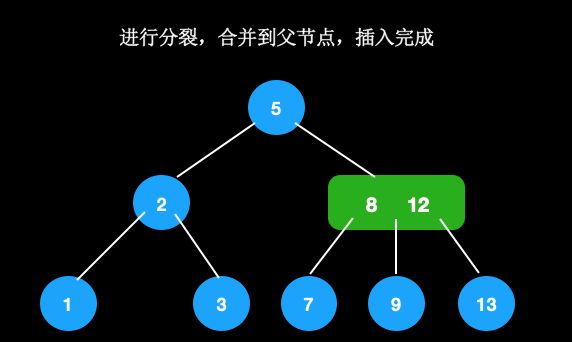
-
进行分裂,合并到父节点,插入完成
-
若
pp为三节点将分裂的节点放到
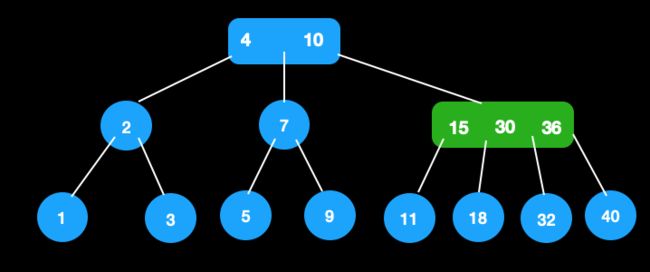
pp中,则pp成为了4节点,不满足定义,那么4-节点需要提出一个值,并向上合并,这时需要重新设置新旧节点的关系。往上合并的过程就是继续套用这几种情况。好的情况是往上的过程中遇到了2节点,且平衡,则结束;坏的情况是一直到根节点,并且根节点是3树,那么只好继续往上分裂出新的根节点,然后处理新节点与其他节点的关系,此时树高增加了1。
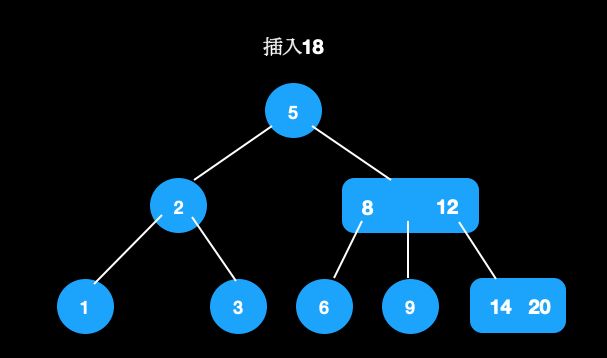
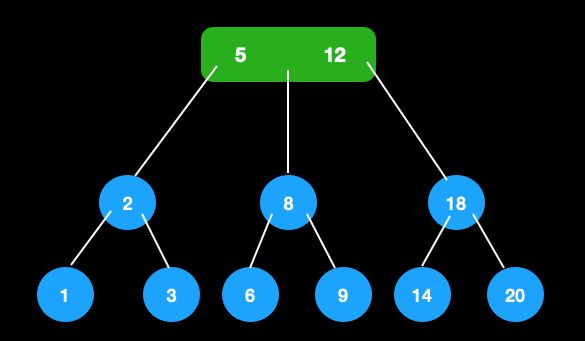
比如在这颗树中插入18。
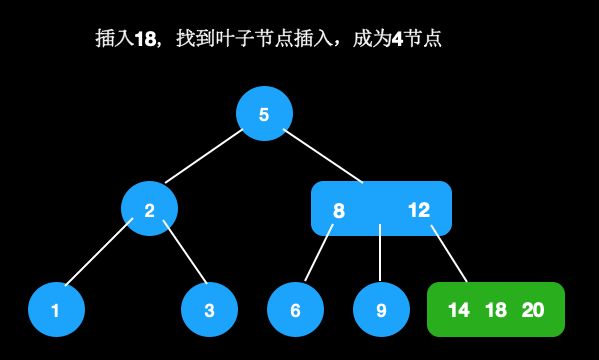
- 插入18,找到叶子节点插入,成为4节点
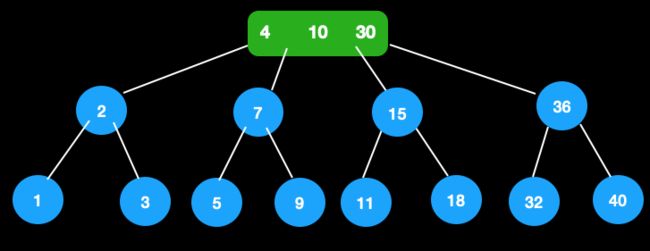
2)向上分裂,将18插入父节点,变成4节点,需继续分裂
3)根节点成为3节点,插入结束
以上的插入,树的高度都没有变化。下面说一种树的高度会+1的情况。
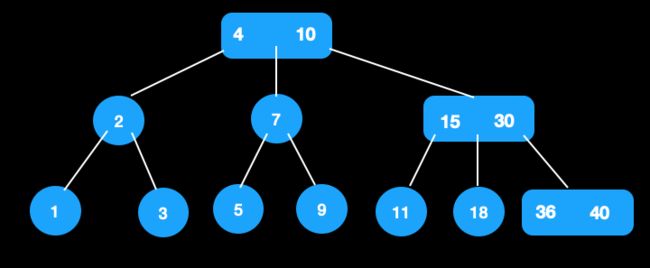
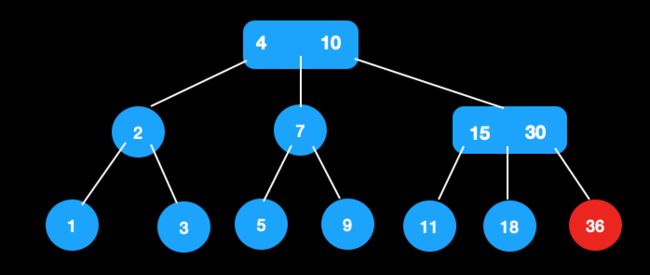
比如在这棵树中插入32。
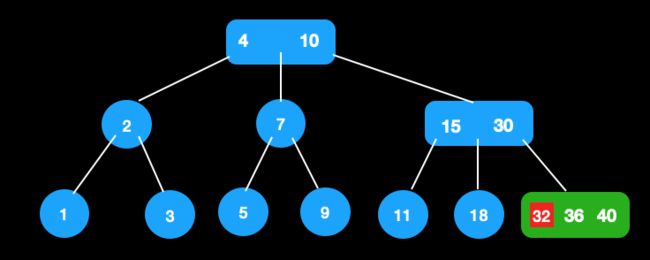
- 找到待插入的节点直接插入32
- 分裂节点,此时父节点变成4节点,还需分裂
- 此时根节点为4节点,需分裂
- 生成新的根节点,树的高度加1
2-3树的删除
删除的情况会复杂一些,下面分几种情况来说。
待删除的值在叶子节点
叶子节点为3节点
直接删除即可。如下图12可直接删除。
删除后,3节点成2节点。
叶子节点为2节点
这里需要区分临近兄弟节点的类型。先将节点删除。
- 兄弟节点为3节点
此时被删除后,节点会为空。通过向兄弟节点借一个最近的键值,然后再调整该节点与父节点的值。
比如在这颗树中删除7。
- 向兄弟节点借最近节点,此时大小关系不满足
- 调整大小,8,9交换,满足定义
-
兄弟节点为2节点,这时需要判断父节点类型
a. 父节点为3节点
此时兄弟节点不够借,父节点降元,从3节点变成2节点,与兄弟节点合并。
比如从这棵树中删除36。
30与18合并,3节点变成2节点,删除完成
b. 父节点为2节点
将父节点和兄弟节点合并,形成新的节点,这是把新节点当做当前节点,不断套用上述几种情况进行调整,直至平衡。这种情况下,若根节点是2节点,树的高度会减1。
例1
从这颗树中删除12
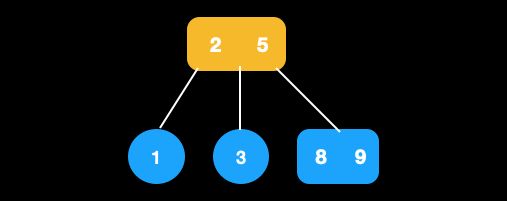
- 兄弟节点和父节点都为2节点,进行合并。此时新节点为[8,9]。
- 当前节点(
[8,9])的父节点和兄弟节点都为2节点,还需进行合并(即节点2,5合并)合并完成如下图。
例2
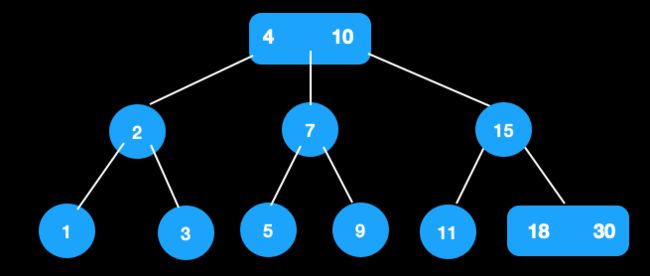
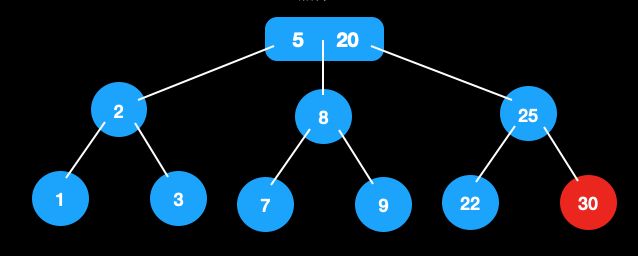
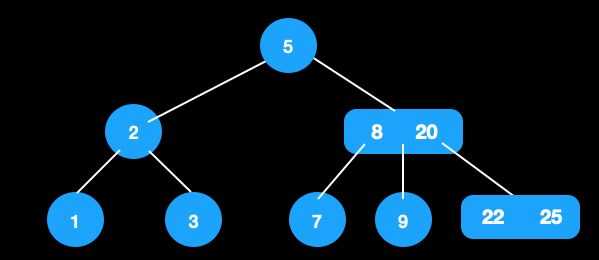
从这棵树中删除30
-
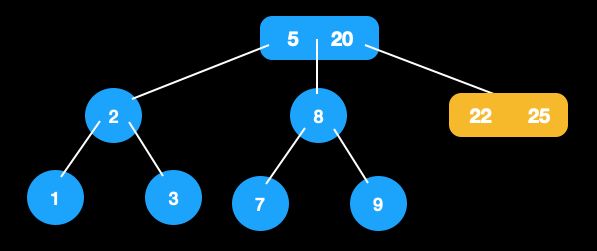
节点30的父节点和兄弟节点为2节点,进行合并,此时[22,25]为新节点。
-
把[22,25]看作当前节点,由于其兄弟节点为2节点,父节点为3节点,套用
2.a中的情况,父节点降元,调整完成。
待删除的值在父节点
将该节点与其前驱或后继节点交换,然后删除交换后的叶子节点,此时转换成上一种情况的处理。
使用中序遍历的顺序,前驱就是指其前一个节点,后继是指其后面的一个节点。最直接的定位如下:
- 前驱节点:该节点左子树最右节点
- 后继节点:该节点右子树最左节点
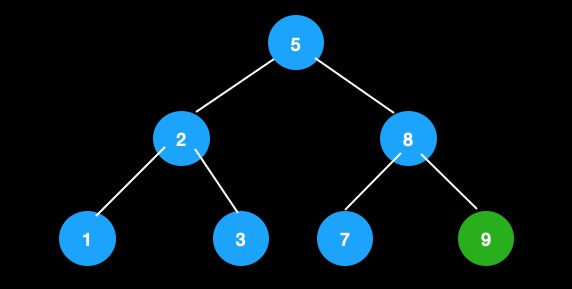
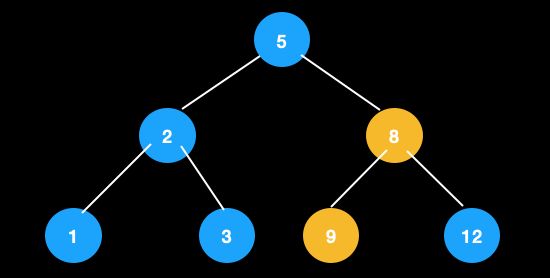
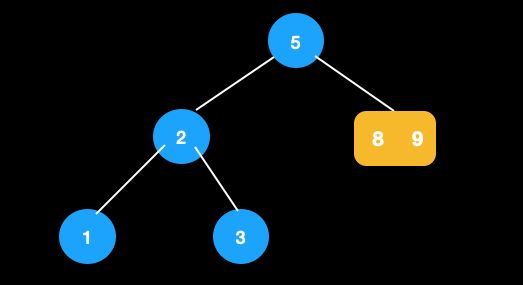
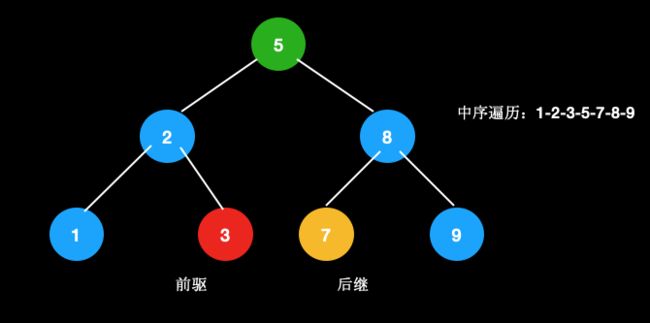
比如下图,5的前驱是3,后继是7。
那为什么要用前驱/后继节点交换呢?
因为,用前驱/后继节点交换后,才能保持大小顺序。后继节点是右子树中最小的节点,与父节点交换后,排除待删除的叶节点,仍保持左子树<新父节点<右子树的关系。同理,前驱节点是左子树中最大的节点,交换后,仍能保持。
这里我们使用后继节点来进行替换。
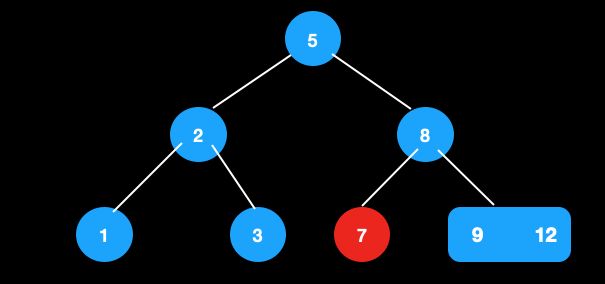
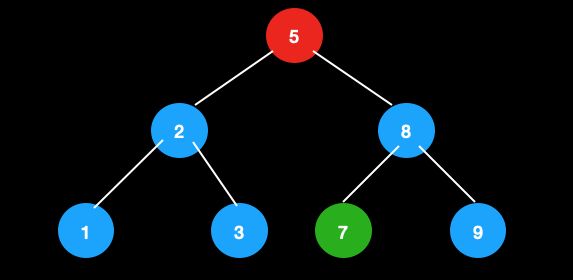
从这颗树中删除节点5。
由于5的后继节点是7,先将值进行交换。这时候目的就是删除叶子节点5,于是可以转换成其父节点和兄弟节点都为2节点的情况进行调整。
红黑树定义
红黑树也是一种二叉平衡树,它满足如下几个特性(根据算法中的定义):
- 根节点是黑色的。
- 红链接均为左链接。
- 从任一节点到其可达叶子节点,经过的黑色节点数量一样(黑平衡)。
- 没有任何一个节点同时与两个红链接相连。
这个定义可能跟我们平常看到的不太一样,由于是以2-3树来理解红黑树,定义红链在左边,这样才能跟2-3树完全对应上。
红黑树与AVL
AVL是一种极度平衡的二叉树,那为什么不用AVL呢?因为AVL插入删除要保持平衡,相比红黑树要慢一些,需要左旋右旋等等。但实际上它的旋转也只是几个场景的套用,哪些场景需要怎么旋转,理解就行了。
而红黑树是近似平衡的(黑平衡),也就是说它不像AVL那样绝对的平衡,所以添加/删除节点后的平衡操作没那么多。
所以对于插入和删除操作较多的场景,用红黑树效率会高一些。
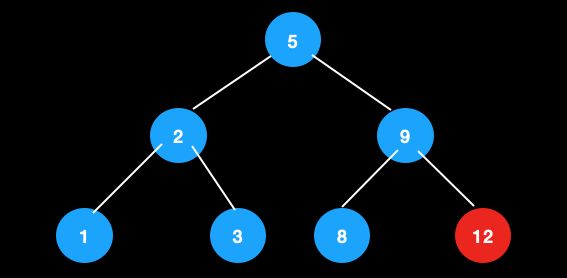
将2-3树转换成红黑树
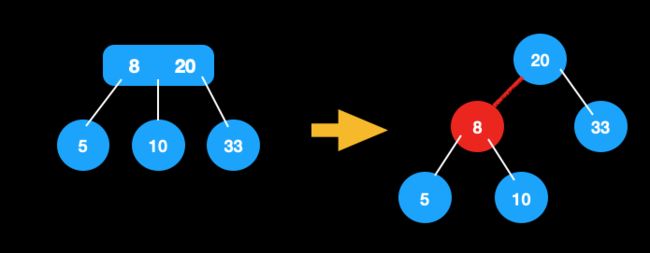
主要思想:3节点分裂成2节点。
将3节点的第一个元素,作为第二个元素的左节点,并用红色的线连接,此时红色线连接的节点就相当于红色。
将2-3树按照以上思想转换后,就得到了一颗红黑树。用这种方式理解是不是简单多了呢?
同时也有几个问题值得我们思考:
-
为什么红链规定在左边呢?
我觉得是前人的一个约定,为了保持统一,简化处理,都放在左边。那都放右边是不是也可以呢?
-
没有任何一个节点同时与两个红链接相连
因为一个红链表示一个3节点,如果有2个红链相连,则表示为4节点,不符合2-3树定义。
-
根节点为黑色
只有3节点的左链才为红色。根节点没有父节点,不可能为红色。
-
根节点到叶子节点经过的黑色节点数目相同
因为2-3树是完美平衡的。红黑树中经过的黑节点数=其层数。
红黑树的应用
-
散列表的冲突处理
map的实现,底层一般会采用红黑树,在节点多的时候效率高。
在节点少的时候,可用链表方式。
- 动态插入、删除和查询较多的场景