SVD(Singular Value Decomposition)奇异值分解
14.1 SVD的应用
利用SVD实现,我们可以用小得多的数据集来表示原始数据集,这样可以去除噪声和冗余信息。所以我们可以把SVD看成从有噪声的数据中抽取相关特征。
14.1.1 隐性语义分析
最早的SVD应用之一就是信息检索。我们称利用SVD的方法为隐性语义索引(LSI)或隐性语义分析(LSA)。在LSI中,一个矩阵有文档和词语组成,当我们在这个矩阵上应用SVD时,就会构建出多个奇异值。这些奇异值代表文档中的概念或主题。
14.1.2 推荐系统
SVD的另一个应用是推荐系统。简单版本的推荐系统是计算物品或用户之间的相似度。更先进的是利用SVD从数据中构建一个主题空间,然后再此空间下计算相似度。
SVD是矩阵分解的一种类型,而矩阵分解是将数据矩阵分解为多个独立部分的过程。
14.2 矩阵分解
很多情况下,数据中的一小段携带了数据集中的大部分信息,其他信息可能是噪声或毫不相关的信息。在线性代数重有很多矩阵分解技术。矩阵分解就是把原始矩阵表示成新的易于处理的形式,可能是两个或三个矩阵的乘积。
不同的矩阵分解技术有不同的性质,适合于不同的应用。SVD是常见是一种矩阵分解技术。它将原始矩阵分解为三个矩阵乘积:A(m*n)=B(m*m)*C(m*n)*D(n*n)。其中,矩阵C只有对角元素,其他元素为0,且其对角元素是从大到小排列的,这些对角元素称为奇异值,它对应了原始矩阵A的奇异值。
在科学和工程中,有这么一个普遍事实:在某个奇异值的数目r之后,其它奇异值就设置为0。这意味着数据集中仅有r个重要特征,其它特征都是噪声或冗余特征。
14.3 利用Python实现SVD
NumPy有一个称为linalg的线性代数工具箱,可以实现SVD。
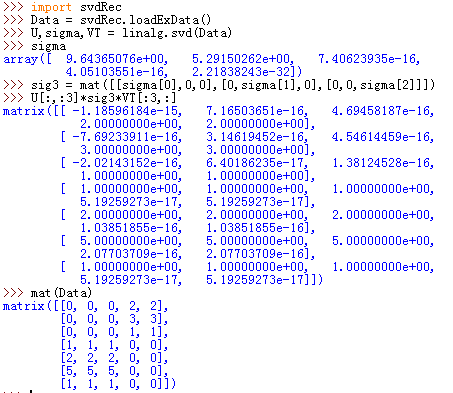
可以看到矩阵Sigma以行向量array形式返回,而非矩阵。因为矩阵非对角元素全是0,这种只返回对角元素的方式可以节省空间。
可以看到,奇异值的前两个比后三个大很多,可以只保留前两个奇异值,然后计算近似矩阵。我们重构了原始矩阵的近似矩阵,只需要用到了矩阵U的前3列和VT的前3行。
如何确定该保留前多少个奇异值呢?两个策略。一:保留矩阵中90%的能量信息,为了计算总能量信息,我们将所有奇异值求平方和,将奇异值的平方和累加到总之的90%即可。二:当有上万个奇异值时,保留前2000或3000个就行,虽然不能保证前3000个奇异值包含90%能量信息,但是如果多数据充分了解,就可以做出类似假设。
有很多应用可以通过SVD来提升性能,比如下面将要讨论的-推荐引擎。
14.4 基于协同过滤的推荐引擎
协同过滤(collaborative filtering)是通过将用户和其他用户数据进行对比来实现推荐的。
当我们知道两个用户或者两个物品的相似度时,就可以利用已有数据来预测未知用户的喜好。所以,问题就在于相似度的计算。
14.4.1 相似度计算
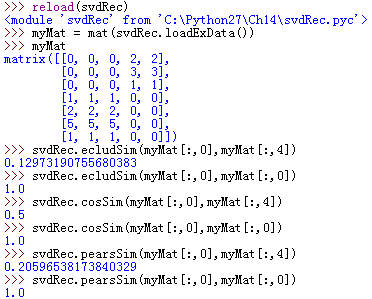
这里相似度计算主要介绍三种方法,并且都将相似度的值归一化到0~1之间。
欧氏距离:字面意思。。。两个向量的欧氏距离。。。相似度=1/(1+距离),使其归一化。
皮尔逊相关系数:度量的是两个向量的相似度,在NumPy中用函数corrcoef()计算得出。使用0.5+0.5*corrcoef()归一化。
余弦相似度:计算两个向量夹角的余弦值。夹角90度,相似度为0,方向相同,相似度为1。
14.4.2 基于物品的相似度还是基于用户的相似度?
大多数情况下,是基于物品的相似度,因为往往用户数量远大于物品数量。
14.5 示例:餐馆菜肴推荐系统
此餐馆推荐系统关注的是餐馆食物的推荐。它可以寻找用户没有尝过的菜肴,通过SVD减少特征空间并提高推荐效果。之后,可以将程序打包通过用户可读的人机交互界面提供给人们使用。
14.5.1 推荐未尝过的菜肴
推荐系统的工作流程是:给定一个用户,系统会为此用户返回N个最好的推荐菜。为了实现这一点,需要做到:
(1)寻找用户没有评级的菜肴,即在用户-物品矩阵中的0值。
(2)在用户没有评级的所有物品中,对每个物品预计一个可能的评级分数。即预测用户可能打出的分数。
(3)对这些物品的评分从高到底排列,返回前N个物品。
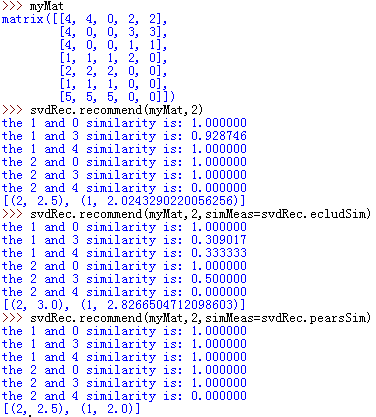
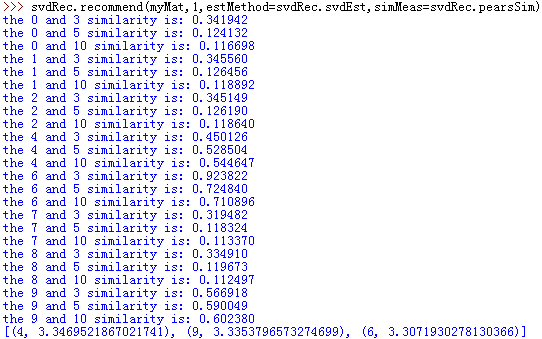
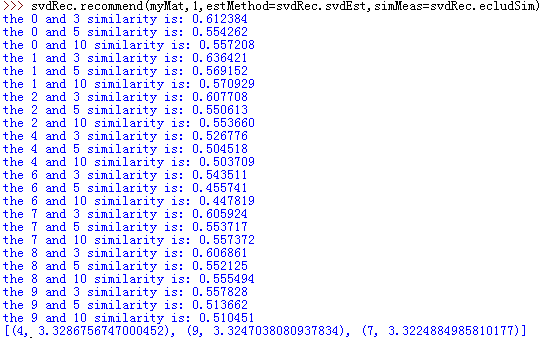
推荐系统对用户2(即myMat矩阵第3行)没有评级的餐馆(即为0值)进行了预测。结果中打印出未评级餐馆与其他餐馆相似度,最终给出对没有评级餐馆的预测评级,并且是按评级分数从大到小排序的。上图试验了三种不同相似度方法下的预测结果。
14.5.2 利用SVD提高推荐效果
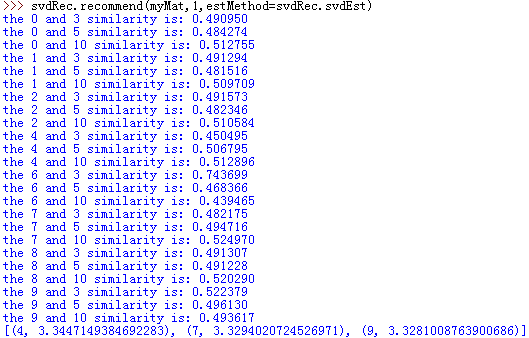
实际的数据集肯定比上一小节用到的大得多,也稀疏的多。下面我们计算一个很大矩阵的SVD来了解到底需要多少维特征。
可以看到有很多奇异值,而前三个奇异值包含了90%以上的总能量。那么我们就可以将之前的高维度矩阵转换成3维矩阵。利用SVD将所有菜肴映射到低维空间中,在低维空间下,我们可以利用前面相同的相似度计算方法来进行推荐。
14.5.3 构建推荐引擎面临的挑战
推荐引擎中存在很多规模扩展性的挑战性问题,比如矩阵表示方法。在实际系统中0的数目非常多,我们可以只存储非零元素来节省内存和计算开销。另一个计算资源浪费是相似度计算得分,每次我们需要一个推荐得分时,都要计算多个物品之间的相似度,而这些信息可以被另一个用户重复利用,所以在实际中,普遍做法是离线计算并保存相似度得分。
推荐引擎面临的另一个问题是如何在缺乏数据时给出好的推荐。这称为冷启动问题。不赘述啦~
14.6 示例:基于SVD的图像压缩
在代码库里,我们有一张手写的数字图像。原始图像大小为32*32=1024像素。我们可以使用SVD来对数据降维,对图像压缩可以节省空间或带宽开销。
imgCompress函数可以基于任意给定的奇异值数目来重构图像。我们给定的是2,即取前两个奇异值来重构图像。得到结果如下:
可以看到,只需要两个奇异值就可以较精确地对图像实现重构。而我们所需要的数字数目是64+64+2=130。和原来的1024个数目相比,获得了几乎10倍的压缩比。
14.7 本章小结
SVD是一种强大的降维工具,我们可以利用SVD来逼近矩阵并从中提取重要特征。通过保留矩阵中80%~90%的能量,就可以得到重要的特征并去除噪声。SVD已经应用到很多应用中,其中之一就是推荐系统。
推荐引擎将物品推荐给用户,协同过滤是一种基于用户喜好或行为数据的推荐的实现方法。协同过滤的核心是相似度计算方法,有很多相似度计算方法都可以用于计算物品或用户之间的相似度。通过在低维空间下计算相似度,SVD提高了推荐系统引擎的效果。
在大规模数据集上,SVD的计算和推荐是一个困难的的工程问题。通过离线方式来进行SVD分解和相似度计算,是一种减少冗余计算和推荐所需时间的方法。下一章会介绍在大数据集上进行机器学习的一些工具。