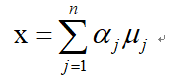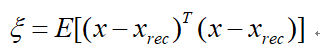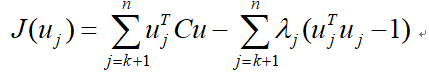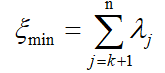维数约减报告
编写人:杨根 黎君玉 张荣华
目录
1 .背景和意义
2.维数约减
3.维数约减的常见方法
4.维数约减应用
5.优缺点
优点
缺点
1 .背景和意义
伴随着科学信息技术水平的不断提高,人们对数据的存储与采集能力的快速提升,使得获取数据变得越来越容易,而数据处理的能力却没有得到较好地改善。在科学研究的诸多领域中,如人脸识别、生物信息学、信息检索、遥感图像处理等都积累了大量的数据。就普遍而言,这些数据具有“高维性”和“海量性”等特点,而且数据构造变得越来越复杂。如果直接对高维数据进行处理时会带“维数灾难”(Curse of Dimensionality)问题;而且,如果样本数小于数据的特征维数时,会导致模型估计的性能恶化,出现所谓的小样本问题。因此,如何挖掘出高维海量的数据中背后蕴藏的符合实际需求有用知识,探索高维数据中隐藏的数据结构和内在分布规律将成为模式识别、机器学习、数据挖掘、计算机视觉等诸多研究领域的极大挑战
在信息化时代,维数约减是高维数据处理的有效手段,其在数据有效降低维度的同时减少数据中的噪声和冗余信息;是人工智能的研究核心之一,在科学研究领域中承担着十分重要的作用。
2.维数约减
维数约减是指将样本从原始输入空间通过某种变换或映射获得原数据集有效子空间的低维表示。维数约减作为高维数据处理的一种有效方式,其对数据降维希望不损失数据的关键特征信息,且同时保留原始数据的潜在的内在结构。维数约减作为数据处理的预处理过程,能够有效的提高后续机器学习的性能和有效的提高分类效果。然而,也会造成一定的信息损失。维数约减方法在用于降维的同时不仅有效的减少数据中冗余信息、噪声信息及不相关的信息,而且能够有效的解决高维数据所带来的维数灾难性问题大大减低数据处理的计算复杂度。在很多的实际情况下,将高维数据的维数的降到一个适当的范围,而且在能尽可能的不破坏初始数据的结构分布,进而有利于对数据的处理。
在收集数据的过程中,数据量大,成千上万,其特征也不一致,一般在各种情况下,我们很难把这些数据理清,但往往数据间也存在某种特别的联系,因此,需要运用维数约减(Dimensionality Reduction)来对这些数据进行去冗余,从而提高机器学习的效率。
定义
维度约减是一种无监督学习,它的实质是去除冗余特征。
对维数约减概述:
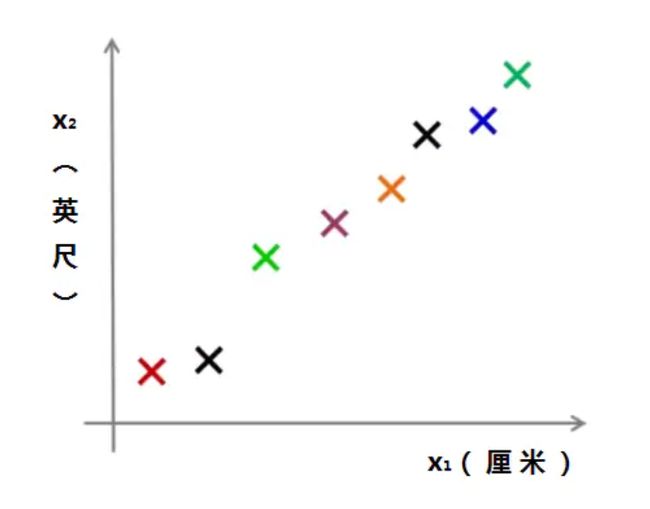
例如厘米和英尺,都是长度的度量,那么:
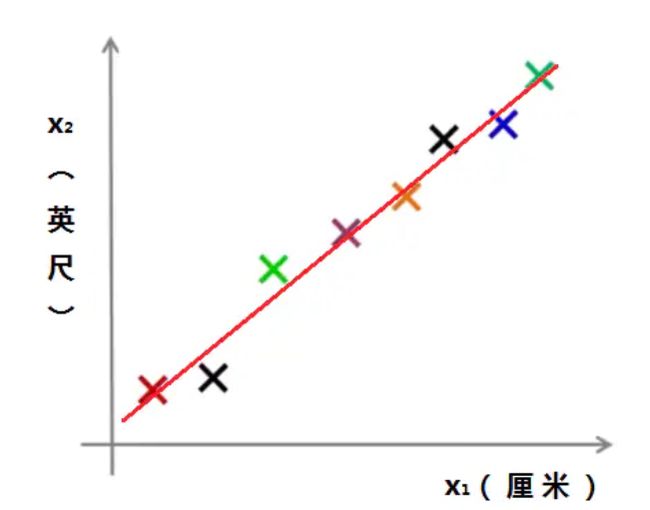
我们可以将这些落点,用一根直线串起来:
出于一些误差的原因,所以落点没有在一根直线上。
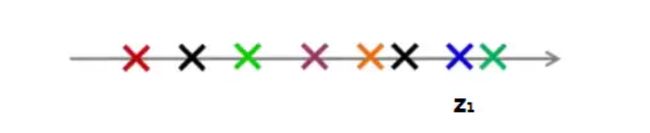
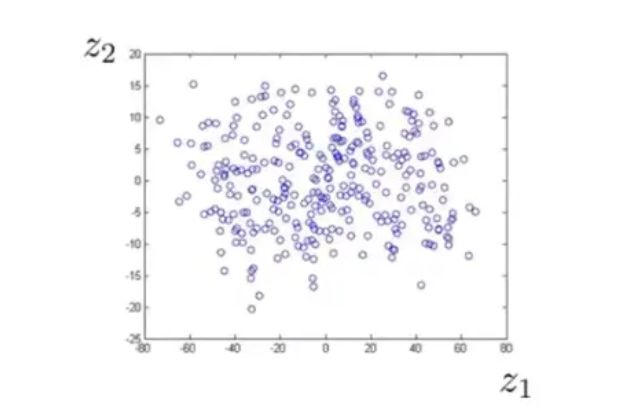
对于这样的情况,我们可以将它从二维压缩到一维:
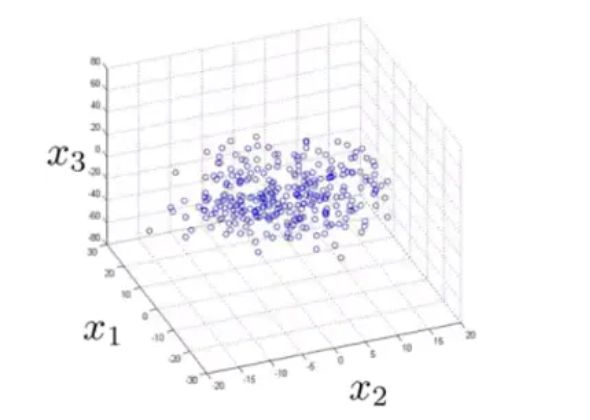
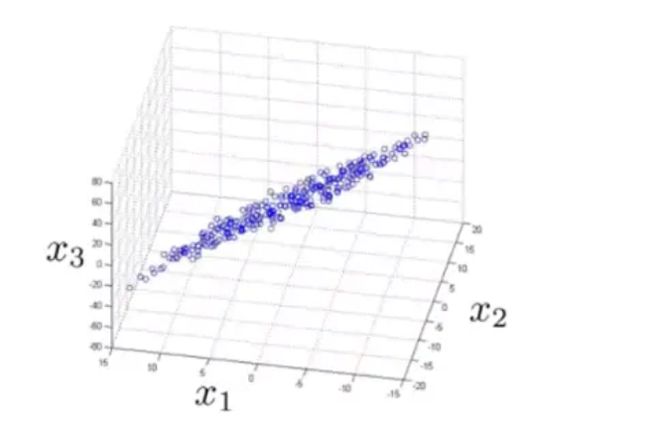
类似的,如果我们有一些三维的数据:
在打印的时候我们发现,这些数据几乎落在了一个平面上:
这也说明其存在一些强相关关系,我们可以将数据从三维降到二维:
3.维数约减的常见方法
降维方法是用来克服“维数灾难”和模型化高维数据的一种典型数据处理技术,是用来解决这一问题的有效手段之一。它可通过对离散数据集合的分析来探求嵌入在高维数据空间中本征低维流形的不同样式,寻求事物的本质规律性。
维数(特征)约减包括两类常用的方法,即特征选择和特征抽取。
特征选择技术其包括信息增益(IG,Information Gain)、互信息(MI,Mutual Information)、CHI(x2统计)、期望交叉熵(ECE,Expected Cross Entrophy)。
特征抽取技术其包括主成分分析(PCA)、FISHER线性判别分析。
主成分分析法是一种数学变换的方法.它把给定的一组相关变量过线性变换转成另一组不相关的变量。这些新的变量按照方差依次递减的顺序排列。在数学变换中保持变量的总方差不变,使第一变量具有最大的方差,称为第一主成分,第二变量的方差次大,并且和第一变量不相关,称为第二主成分。依次类推,i个变量就有i个主成分。
从代数角度,即将原变量的协方差矩阵转换成对角矩阵。从几何角度,将原变量系统变换成新的正交系统,使之指向样本点散布最开的正交方向,进而对多维变量系统进行降维处理。按照特征提取的观点,主成分分析相当于一种
基于最小均方误差的提取方法。下面给出主成分分析的详细介绍:
设n维空间的随机向量用伊,c,o∈R2表示,将![]() 进行零均值处理,
进行零均值处理,![]() ,则E(x)=0。如果对x用一组完备的正交基uj,j=1,2,,n展开,可得
,则E(x)=0。如果对x用一组完备的正交基uj,j=1,2,,n展开,可得
假设只用前K项进行重构,则
其均方误差为
因为
所以
是x和![]() 的总体协方差矩阵。为了使重构的均方误差最小,并满足正交条件的约束,采用拉格朗日乘子法,将函数
的总体协方差矩阵。为了使重构的均方误差最小,并满足正交条件的约束,采用拉格朗日乘子法,将函数
对于![]() ,j=k+1,....,n求导,得
,j=k+1,....,n求导,得
令k=1,此时u1,....,un。为总体协方差矩阵C的本征向量,![]() 分别是它们对应的本征值,这些本征向量经过正交化处理所张成的空间称为本征空间。将本征向量u1,....,un。按照它们的本征值进行降序排列,则得到结论:
分别是它们对应的本征值,这些本征向量经过正交化处理所张成的空间称为本征空间。将本征向量u1,....,un。按照它们的本征值进行降序排列,则得到结论:
对于任一随机向量x,如果采用总体协方差矩阵C的前k个最大且非零本征值所对应的本征向量作为坐标轴展开,可在相等截断长度下获得所有正交展开中最小的截断均方误差![]() :
:
上述的变换称为KL展开,可用于任意随机变量。随机向量x的第i主成分分量可表示为
4.维数约减应用
1. 数据预处理是机器学习和数据挖掘的重要组成部分:机器学习中的数据量往往是巨大的,降维是缩小数据规模的有效方法。
2. 大多数机器学习和数据挖掘技术可能对高维数据均无效,随着维度的增加,查询的准确性和效率会迅速下降。
3. 可视化:将高维数据投影到2D或3D上。
4. 数据压缩:高效的存储和检索。
5. 噪声消除:准确查询。
5.优缺点:
优点:
它有助于数据压缩,从而减少存储空间。
它减少了计算时间。
它还有助于删除多余的功能(如果有)。
缺点:
这可能会导致一定程度的数据丢失。
PCA倾向于发现变量之间的线性相关性,这有时是不可取的。
如果均值和协方差不足以定义数据集,则PCA失败。
我们可能不知道要保持多少个主要组成部分,是否应用了一些经验法则。
![]()