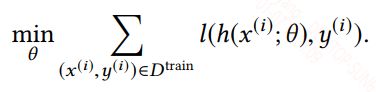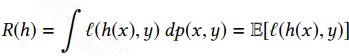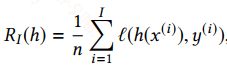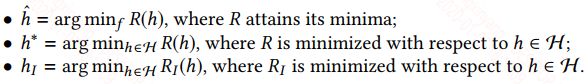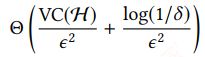FSL（小样本学习）综述——Generalizing from a Few Examples: A Survey on Few-Shot Learning

1，引言

　　现在的机器学习和深度学习任务都依赖于大量的标注数据来训练，而人类的学习过程并不是这样的，人类可以利用过去学得的知识，在新的问题上只需要少量的样例就可以学得很好。FSL就是这样一个任务，期待像人类一样，能利用一些先验知识，在新的问题上只需要少量样本。

2，概述

　　本节给出了FSL的定义，并且根据机器学习中的误差分解理论，认为FSL任务中最小化经验风险是不可信的，这也是FSL难以训练的原因

　　2.1 Notation

　　对于一个FSL任务T，给定一个数据集$D = {D^{train}, D^{test}}$，包含训练集$D^{train} = {x^i, y^i} i=0,...,I$ （$I$是一个很小的数据集）和测试集$D^{test} = {x^{test}}$。通常而言将FSL考虑为一个N-way K-shot的分类任务，假定任务的真实分布为$p(x, y)$。而对于这个真实分布有一个最优假设（hypothesis）$\hat{h}$可以描述它。我们现在需要的是去求出这个最优假设，但是很难求出来，通常的做法是给定一个假设空间$H$，然后从里面找一个接近$\hat{h}$的假设$h$，在这里$H$是由你选择的模型和参数的初始化分布决定的，而$h$的寻找过程起始就是一个优化过程，而通常的优化方法就是梯度下降。这里其实是对一个机器学习过程的描述，只不过当训练集非常少的时候，可以将问题转化为FSL。

　　2.2 Problem Definition

　　在经典的机器学习中，给定一个任务T，任务的性能P，给定一些额外的条件E，比如标注的训练数据，可以提升任务T的性能P。FSL任务其实本质上也是这样的，这里给出一些FSL相应的形式，比较简单，直接看论文吧

　　2.3 Relevant Learning Problems

　　大多数人认为FSL就是meta learning，其实不是。FSL可以是各种形式的学习，监督，半监督，强化学习，迁移学习等等，本质上的定义取决于可用的数据。但现在大多数时候在解决FSL任务时，采用的都是meta Learning。

　　2.4 Core Issue

　　在机器学习中寻找最适合的假设时通常都是通过找到一组最优的参数来确定这个假设，并通过给定的训练集，最小化损失函数这一目标来指示最优参数的搜索，最小化损失函数如下所示：

　　　　

　　在训练模型中，我们是通过训练集来拟合真实分布，我们训练出来的分布和真实分布往往不一样，这中间的差值称为期望风险（期望损失），表达式如下：

　　　　

 　　理论上说，让期望风险最下化才能逼近真实分布，但因为你并不知道真实分布，所有最小化期望风险是无法实现的，而在机器学习中通常用经验风险来替换期望风险，经验风险就是在训练集上预测的结果和真实结果的差异，也是我们常说的损失函数，表达式如下：

　　　　

　　我们给出下面一个符号描述：

　　　　

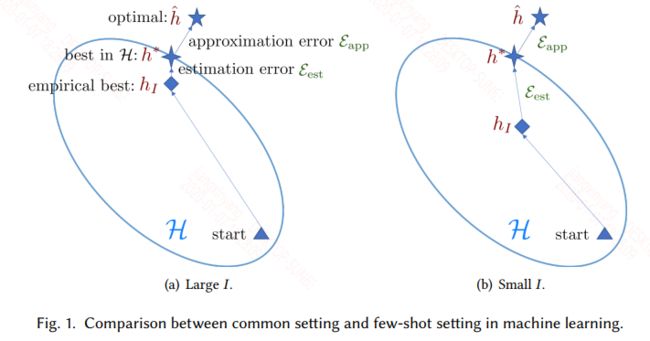
 　　$\hat{h}$是真实分布的假设，$h^*$是假设空间$H$中最接近$\hat{h}$的假设，而$h_I$是你通过最小化经验损失得到的假设。根据机器学习中的误差分解可得：

　　　　

　　等式右边第一项表示的是假设空间$H$中最优的假设和真实假设的误差，这一项其实由你所选择的模型和参数的初始化分布决定的，这也就是为什么有的时候，模型选择的简单了，你给再多的数据也训练不好，欠拟合。第二项就是我们训练得到的假设和$H$中最优假设的误差，我们训练得到的假设也是从假设空间$H$中选择的，但有时候会陷入局部最优，或者提供的训练数据分布有偏差，导致无法到全局最优。

　　但理论上对于第二项，当样本数量$I$足够大时，有：

　　　　

 　　传统的机器学习都是建立在大规模的训练数据上的，因此$\varepsilon_{est} (H, I)$是很小的，但是在FSL任务上，训练数据很小，因此$\varepsilon_{est} (H, I)$是很大的，所以此时采用传统的训练模式，如softmax+交叉熵，是极容易陷入过拟合的。具体的图如下：

　　　　

　　针对上面的问题再去拓展寻求解决方案，在机器学习中正则化是一项，正则化可以约束你的假设空间$H$，但是在FSL中不行，它的约束是没有指示性的，而FSL中的约束是需要有指示性的，即能指示你更好的接近真实假设。引入霍夫丁不等式：

　　　　

　　给定样本复杂度为S，保证上述不等式能在$\epsilon$很小且$\delta$很小时成立时，需要给定的样本数I大于S，给定VC维理论：

　　　　

　　2.5 Taxonomy

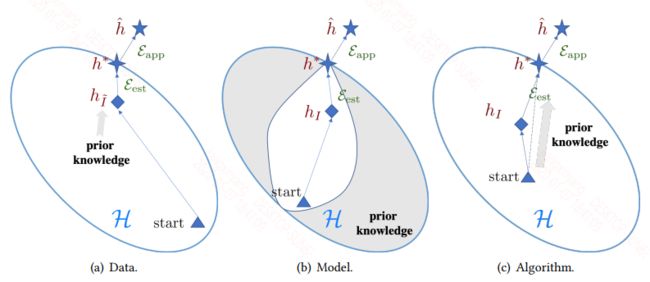
　　根据林轩田的机器学习，样本的复杂度S理论上需要等于10000VC，但实际上等于10VC就能较好的训练，从这面来看当模型复杂度较高时，也就是VC维较高时，比如现在的深度学习模型，这样就需要大量的样本才能训练好。而在FSL任务中就期待使用先验知识来弥补样本的不足。在这里作者将解决这个问题的方法分为了三类：Data，Model，Algorithm。具体的图如下：

　　

　　Data

　　Data就是通过先验知识来做数据增强，数据量增大自然能解决上述问题。

　　Model

　　通过先验知识来限制模型复杂度，降低假设空间$H$的大小，减小VC维，使得当前的数据集可以满足

　　Algorithm

　　通过先验知识来提供一个好的搜索策略，可以是一个好的搜索起始点，也可以是一个明确的搜索策略，来寻找最优点。

　　接下来的工作都是围绕这几个方向展开来求解FSL问题。

　　　　

3，DATA

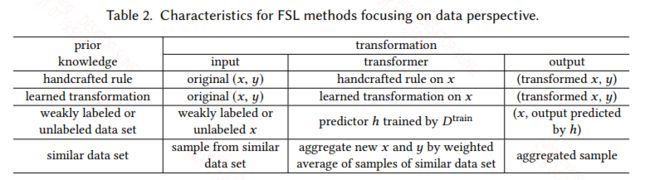
　　数据增强的方式有很多种，平时也被使用的比较多，在这里作者将数据增强的方法概括成4类：

　　　　

　　总之，数据增强没有什么神秘感，也是大家比较熟悉的，无论是手动在数据上修改，比如图片的旋转，句子中的同义词替换等，以及复杂的生成模型生成和真实数据相近的数据。数据增强的方式有很多种，大量的合适的增强一定程度上可以缓解FSL问题，但其能力还是有限的。

4，MODEL

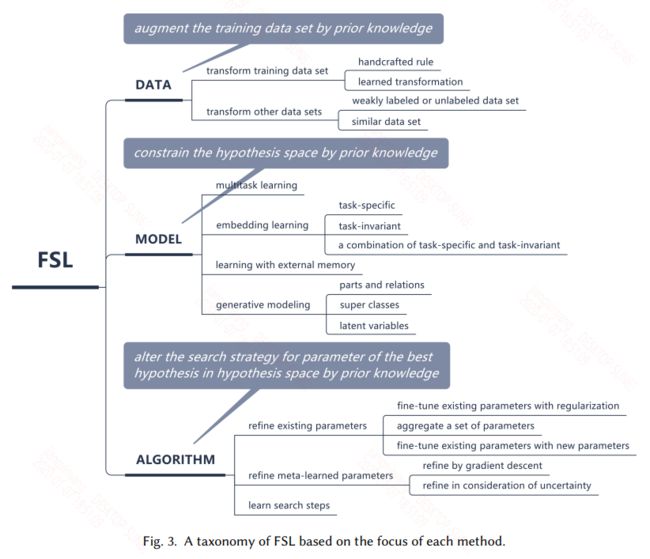
　　如果我们想使用机器学习模型来解决FSL问题，我们需要使用假设空间$H$很小的模型，这样样本复杂度也就小了，对于一些简单的任务，这样是可行的，但是对于复杂的任务，小的模型会导致$\varepsilon_{app} (H)$很大，而现实中大多数任务都很复杂，它们的特征很多，且特征维度也很高。因此我们只能一开始给一个假设空间$H$很大的模型，然后通过一些先验知识将这个空间中无效的hypothesis去掉，缩小假设空间$H$，这样做感觉很绕，但实际上和模型剪枝中的理念类似，你一开始给一个小的模型，这个模型空间离真实假设太远了，而你给一个大的模型空间，它离真实假设近的概率比较大，然后通过先验知识去掉哪些离真实假设远的假设。

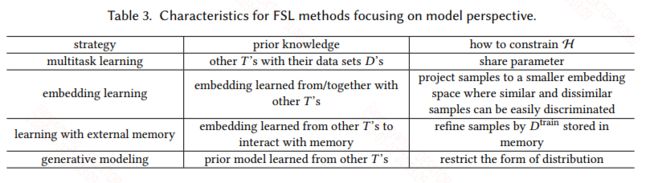
　　作者根据使用不同的先验知识将MODEL的方法分成4类：

　　　　

 　　4.1 Multitask Learning

　　多任务学习也是比较常见的，对于多个共享信息的任务，可以是数据相同任务不同，也可以是数据和任务都不同，但是数据具有领域性等等，都可以用多任务学习来训练，多任务分为硬参数共享和软参数共享两种模式：

　　　　

　　硬参数共享认为任务之间的假设空间是有部分重叠的，体现在模型上就是有部分参数是共享的，而共享的参数可以是模型的前面一些层，表征任务的低阶信息。也可以是在嵌入层之后，不同的嵌入层将不同任务嵌入到同一不变任务空间，然后共享模型参数等等。

　　软参数共享不再显示的共享模型参数，而是让不同的任务的参数相似，这就可以通过不同任务的参数正则，或者通过损失来影响参数的相似，以此让不同任务的假设空间类似。

　　多任务通过多个任务来限制模型的假设空间，对于硬参数共享，多个任务会有一个共享的假设空间，然后每个任务还有自己特定的假设空间；对于软参数共享也类似，软参数更灵活，但也需要精心设计。

　　4.2 Embedding Learning

　　嵌入学习很好理解，将训练集中所有的样本通过一个函数$f(.)$嵌入到一个低维可分的空间$Z$，然后将测试集中的样本通过一个函数$g(.)$嵌入到这个低维空间$Z$，然后计算测试样本和所有训练样本的相似度，选择相似度最高的样本的标签作为测试样本的标签，根据task-specific和task-invariant，以及两者的结合可以分为三种，嵌入学习如下：

　　　　

　　Task-specific是在任务自身的训练集上训练的，通过构造同类样本相同，不同类样本不同的样本对作为数据集，这样数据集会有一个爆炸式的扩充，可以提高样本的复杂度，然后可以用如siamese network等来训练。

　　Task-invariant是在一个大的且和任务相似的source 数据集上训练一个嵌入模型，然后直接用于当前任务的训练集和测试集嵌入。

　　但实际上现在用的比较多的还是两者的结合，既可以利用大的通用数据集学习通用特征，又可以在特定任务上学习特定的特征，而现在常用的训练模式是meta learning中的metric-based的方式，此类常见的模型有match network，prototypical network ，relation network等，详细可以见小样本学习（few-shot learning）在文本分类中的应用。

　　4.3 Learning with External Memory

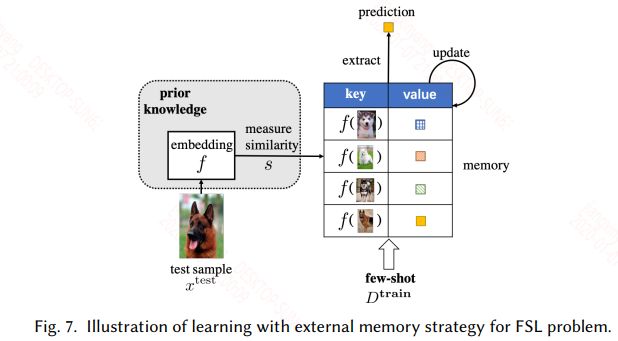
　　具有外部存储机制的网络都可以用来处理这一类问题，其实本质上和迁移学习一样，只不过这里不更新模型的参数，只更新外部记忆库，外部记忆库一般都是一个矩阵，如神经图灵机，其外部记忆库具有读些操作，在这里就是在一个用大量类似的数据训练的具有外部存储机制的网络上，用具体task的样本来更新外部记忆库。具体的如下图所示：

　　　　

 　　这类方法需要精心设计才能有好的效果，比如外部记忆库写入或更新的规则可能就影响模型能够在当前任务上的表现。

　　4.4 Generative Modeling

　　引入了生成式的模型来解FSL问题，不是很熟，跳过了。

5，ALGORITHM

　　在机器学习中我们通常使用SGD以及它的变体，如ADAM，RMSProp等来更新参数，寻找最优的参数，对应到假设空间$H$中最优的假设$h^*$。这种方式在有大量的数据集的情况下可以用来慢慢迭代更新寻找最优参数，但是在FSL任务中，样本数量很少，这种方法就失效了。在这一节，我们不再限制假设空间。根据使用不同的先验知识，可以将ALGORITHM分为下面3类：

　　　　

　　5.1 Refine Existing Parameters ${\theta} ^ {0}$

　　这一小节的本质上就是我们常用的pretrained + fine-tuning的模式，最常见的就是直接在pretrianed的模型上直接fine-tuning参数，其他的还有可以在一个新的网络上使用pretrained的部分参数来初始化等等。

　　5.2 Refine Meta-learned $\theta$

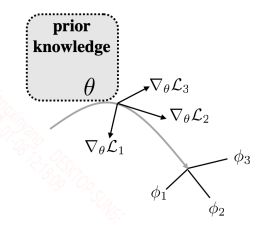
　　该小节是基于meta learning的解决方法，利用元学习器学习一个好的初始化参数，之后在新的任务上，只要对这个初始化参数少量迭代更新就能很好的适应新的任务。这种方法最经典的模型就是MAML，MAML的训练模式如下图所示：

　　　　

 　　上面的参数$\theta$是元学习器的参数，而$\nabla_{\theta}L_1$是任务1得到的梯度，其他的同理，最后用多个任务的梯度矢量和来更新参数$\theta$。具体的算法如下：

　　　　

 　　元学习区别于机器学习的是，机器学习通常是在拟合一个数据的分布，而元学习是在拟合一系列相似任务的分布，因此元学习的训练样本其实是一系列任务，如上面的算法：

　　1，从任务集中采样batch个任务

　　2，每个任务的数据集都分为训练集和测试集，遍历所有的任务，首先用每个任务的训练集得到一个更新后的参数${\theta} ^{'}$。这个参数不会直接赋给$\theta$。而是被缓存起来

　　3，用每个任务的测试集在每个任务特有的参数${\theta} ^{'}$上得到一个梯度值

　　4，将上面batch个任务的测试集得到的梯度值的矢量和来更新元学习器的参数$\theta$

　　上面的训练方式可以认为在每个任务中的训练集得到每个任务特定的最优假设，但元学习本质上是要寻找一个对于所有任务都较优的假设，因此在更新参数的时候是结合了所有任务在测试集上的损失来指定梯度更新的。因此这样得到的参数$\theta$在新的任务上已经是一个较优的假设，只需要较少的迭代更新就能达到最优假设。但这样的方式也有一个问题，就是新的任务的特性必须要和元训练中的任务相近，这样$\theta$值才能作为一个较好的初始化值。否则效果会很差。因此也就有不少研究在根据新任务的数据集来动态的生成一个适合它的初始化参数。

　　5.3 Learn Search Steps

　　上一节使用元学习来获得一个较好的初始化参数，而本节旨在用元学习来学习一个参数更新的策略。这类问题最经典的就是“Learning to learn by gradient descent by gradient descent ”。至于为什么要这样做，是因为在现代机器学习中大多数都采用人工指定的优化算法，如SGD，ADAM等，这些优化器都是利用了一阶梯度来更新模型，有的用到二阶梯度的信息来控制学习速率的变化。根据“没有免费的午餐定理”知道没有哪一个优化器的效果绝对的好于随机策略，因此针对每一个子任务能给定特定的优化方式实际上是提高性能的唯一方法，这里就是设计一个元优化器来为特定的任务提供特定的优化方法，具体的如下图所示：

　　　　

　　梯度的更新也可以写成：

　　　　

 　  上面式子中$g_t (.)$就是通过元学习器训练出来的优化方法。在这里使用RNN来实现，因为RNN具有时序记忆功能，而梯度迭代的过程中正好是一个时序操作。

　　具体的训练如下图所示：

　　　　

　　训练过程大致如下：对于每个任务，同样划分训练集和测试集，训练集经过meta-learner得到一系列的梯度，因为RNN每个时刻都有输出，因此每个时刻的梯度都去依次更新learner的参数$\phi$。这样看就相当于一个batch的样本就更新了T词learner。训练完一轮之后，用测试集在learner上的到的梯度来更新meta-learner的参数$\theta$。一种交互迭代的训练模式。其实这个和上一节面临的问题一样，meta-learner学到的更新策略是针对这一类任务的，一旦新任务和元训练中的任务偏差较大时，这种更新策略可能就失效了。

6，FUTURE WORKS

　　未来的方向可以从使用的先验数据，例如利用更多的先验知识，多模态的数据等；使用的模型方法，用一些新的网络结构去替换以前的，比如用transformer替换RNN会不会有更好的结果；使用的场景，现在FSL也只是在字符识别，图像识别等取得不错的效果，在CV其他方向，如目标检测，目标跟踪，NLP中的各项任务上又是什么样的表现，该怎样改进；理论分析等。

 

参考文献

Generalizing from a Few Examples: A Survey on Few-Shot Learning 

Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks 

Learning to learn by gradient descent by gradient descent