订餐系统之地图订餐

　　离上一篇博客已经是1月有余了，这中间清楚的认识到自己几年的编程下来（大学4年，入行3载），能拿出手的东西真的屈指可数，也许真的是，一直以来都是为实现功能来写代码，所以终无大的突破！每每得空便思考自己到底差在哪？是不了解框架？于是学习EF；是不了解node.js？安装后，写了些demo; 是没学习新知识？于是学了下WFP... 然而，了解这些东西并没让自己有所收获，反而越发不知所措了。思考还在继续，”探索“还在继续... 于是有一天看到了设计模式，看到《大话设计模式》 才明白自己差在哪，差在对面向对象的理解！于是才开始正式的去了解什么是面向对象，为了加深理解，又细细看了《你必须知道的.net(第二版)》中的OO大原则，OO大智慧，OO之美...而后，再一次对《大话设计模式》中内容细细品味...这时，我觉得自己才开始真正的沉淀了！罗嗦了半天，下面开始今天的正文吧！

　　所谓地图订餐就用户直接在地图上确定自己的位置后，搜索出附近商家后，直接选择商家开始订餐。目前市面上也有很多这样的功能，下面我就把自己实现方式介绍下吧。上篇博客《订餐系统之按距离[根据经纬度]排序、搜索》中所提到的功能，在地图订餐中就是一个应用。

　　注：以下代码都是百度地图的API。google API变成3.0后，语法变了太多了，大部分项目都变成百度地图了。

商家定位

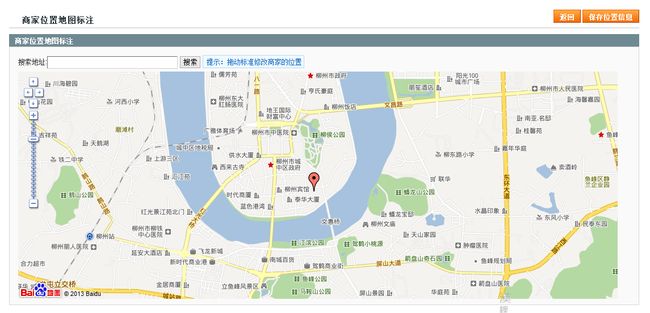
 　　所谓定位，就是在地图上标注商家的位置，成为用户搜索的来源，如图1：

                                                                            图1

 　　定们代码比较简单，js部分代码如下：

View Code

 

商家设置配送范围

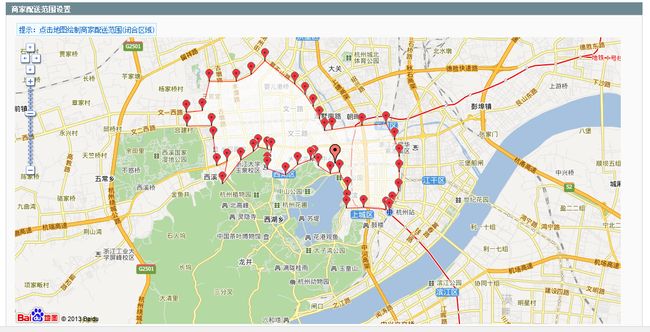
 　　所谓设置配送范围，就在地图上通过标注，绘制出一个多边形区域，如图2：

       　　　　　　　　　　　　　　　　　　　　　　　　　　 图2

　　以下为绘制多边形，js部分代码。页面中只多了几个HiddenField，用来保存坐标、原多边形信息以及一个用于放地图的div。

View Code

 

　　设置好商家的位置，范围后，用户就可以在地图上定好自己的位置，开始搜索商家。搜索分两种方式：1.以当前用户地址为中心，搜索N公里内的商家；2.搜索当前坐标在商家设置的多边形内的商家。以下的地图拉框搜索以及按配送范围搜索就分别是用这种方式来实现的。

 

地图拉框搜索

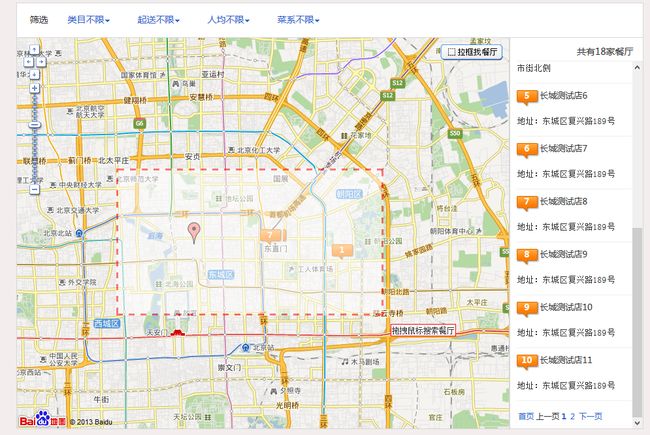
 　　所谓拉框搜索，就是在地图上拉出一个框，只搜索这个框内的商家。当然拉出的是一个长方形，搜索是转换成一个圆，按半径搜索。如图3：

　　 　　　　　　　　　　　　　　　　　　　　　　　　图3

　　
　　拉框部分主要用了api之RectangleZoom.js 只是修改了完成时的事件，这个是从一个论坛中认识的朋友那得来的---程序员真是大多数是好人呐！在548行左右，代码如下：

 var startlng = Math.min(northEastPoint.lng,southWestPoint.lng);
                  var endlng = Math.max(northEastPoint.lng,southWestPoint.lng);
                  var startlat = Math.min(northEastPoint.lat,southWestPoint.lat);
                  var endlat = Math.max(northEastPoint.lat,southWestPoint.lat);
                  var startlgt = endlng - (endlng - startlng)/2;
                  var startlat = endlat - (endlat - startlat)/2;
                  var radius = Math.max((endlng - startlng)/2,(endlat - startlat)/2)*111;
                  GetMapInfo('1',startlgt,startlat,radius);//这里调用自己获取数据方法

修改部分代码

 　　然后再加上API之RichMarker_min.js，这个使用比较简单，基本代码如下：

//地图上添加marker
//参数说明：togoname , picture,address,reviewcont,BookPercapita(人均).shopid
function createMarker(index, togoname, picture, address, reviewcont, BookPercapita, shopid, point) {
    var infohtml = "";

    var htm1 = "
" + togoname + "\">
" + parseInt(index) + "\">" + parseInt(index) + "
" + parseInt(index) + "\" class='markerlabel'>";
    var shopmarker = new BMapLib.RichMarker(htm1, point);

    var temptipinfo = getInfohtml(index, togoname, picture, address, reviewcont, BookPercapita, shopid);
    $("#tipcontainer").append("
" + index + "\">" + temptipinfo + "");

    shopmarker.addEventListener("click", function(e) {
        var shopinfohtml = getInfohtml(index, togoname, picture, address, reviewcont, BookPercapita, shopid);
        var shopinfoWindow = new BMap.InfoWindow(shopinfohtml);
        map.openInfoWindow(shopinfoWindow,point);
    });
    allmarkers.push(shopmarker);
    points.push(point);

    return shopmarker;
}

生成图标代码

　　最终形成了，现在的界面

按配送范围搜索

　　这部分其实主要就是用一个射线法，判断点是否在多边形内，这是我头头写的，不过不怎么准确，在这里我也帖下代码，也希望哪个朋友有更精确的方法提出来。

using System;
using System.Collections;
using System.Collections.Generic;
using System.Configuration;
using System.Data;
using System.Linq;
using System.Web;
using System.Web.Security;
using System.Web.UI;
using System.Web.UI.HtmlControls;
using System.Web.UI.WebControls;
using System.Web.UI.WebControls.WebParts;
using System.Xml.Linq;
using System.Reflection;
using System.Text;

using System.Drawing;
using System.Drawing.Drawing2D;

public static class hjmap
{
    const double INFINITY = 1e10;
    const double ESP = 1e-5;
    const int MAX_N = 1000;

    public struct XPoint
    {
        public double x, y;

        public XPoint(double _x, double _y)
        {
            x = _x;
            y = _y;
        }
    };

    public struct LineSegment
    {
        public XPoint pt1, pt2;
    };

    /// 判断点在多边形内
    /// 

    /// 如果点在多边形内： 返回0
    /// 如果点在多边形边上： 返回1
    /// 如果点在多边形外： 返回2
    /// 
    /// 多边形顶点
    /// 当前点
    /// 
    public static int InPolygon(XPoint[] polygon, XPoint point)
    {
        int n = polygon.Length;
        int count = 0;
        LineSegment line;
        line.pt1 = point;
        line.pt2.y = point.y;
        line.pt2.x = -INFINITY;
        for (int i = 0; i < n; i++)
        {
            //得到多边形的一条边
            LineSegment side;
            side.pt1 = polygon[i];
            side.pt2 = polygon[(i + 1) % n];
            if (IsOnline(point, side))
            {
                return 1;
            }
            // 如果side平行x轴则不作考虑
            if (Math.Abs(side.pt1.y - side.pt2.y) < ESP)
            {
                continue;
            }
            if (IsOnline(side.pt1, line))
            {
                if (side.pt1.y > side.pt2.y)
                    count++;
            }
            else if (IsOnline(side.pt2, line))
            {
                if (side.pt2.y > side.pt1.y)
                    count++;
            }
            else if (Intersect(line, side))
            {
                count++;
            }
        }
        if (count % 2 == 1)
        {
            return 0;
        }
        else
        {
            return 2;
        }
    }

    // 计算叉乘 |P0P1| × |P0P2|
    public static double Multiply(XPoint p1, XPoint p2, XPoint p0)
    {
        return ((p1.x - p0.x) * (p2.y - p0.y) - (p2.x - p0.x) * (p1.y - p0.y));
    }

    // 判断线段是否包含点point
    public static bool IsOnline(XPoint point, LineSegment line)
    {
        return ((Math.Abs(Multiply(line.pt1, line.pt2, point)) < ESP) &&
        ((point.x - line.pt1.x) * (point.x - line.pt2.x) <= 0) &&
        ((point.y - line.pt1.y) * (point.y - line.pt2.y) <= 0));
    }

    // 判断线段相交
    public static bool Intersect(LineSegment L1, LineSegment L2)
    {
        return ((Math.Max(L1.pt1.x, L1.pt2.x) >= Math.Min(L2.pt1.x, L2.pt2.x)) &&
        (Math.Max(L2.pt1.x, L2.pt2.x) >= Math.Min(L1.pt1.x, L1.pt2.x)) &&
        (Math.Max(L1.pt1.y, L1.pt2.y) >= Math.Min(L2.pt1.y, L2.pt2.y)) &&
        (Math.Max(L2.pt1.y, L2.pt2.y) >= Math.Min(L1.pt1.y, L1.pt2.y)) &&
        (Multiply(L2.pt1, L1.pt2, L1.pt1) * Multiply(L1.pt2, L2.pt2, L1.pt1) >= 0) &&
        (Multiply(L1.pt1, L2.pt2, L2.pt1) * Multiply(L2.pt2, L1.pt2, L2.pt1) >= 0));
    }

    /// 判断点在多边形内
    /// 

    /// 如果点在多边形内： 返回0
    /// 如果点在多边形边上： 返回1
    /// 如果点在多边形外： 返回2
    /// 
    /// 定点集合，以30.192353,120.164766|30.192712,120.175851|30.189668,120.170192的方式存在
    /// 当前点
    /// 
    public static int InPolygon(string _lat, string _lng, string _polygon)
    {
        XPoint mypoint = new XPoint();
        mypoint.x = Convert.ToDouble(_lat);
        mypoint.y = Convert.ToDouble(_lng);

        string Polygon = _polygon;

        string[] PolygonArray = Polygon.Split('|');
        hjmap.XPoint[] curvePoints = new hjmap.XPoint[PolygonArray.Length - 1];

        for (int i = 0; i < PolygonArray.Length - 1; i++)
        {
            string[] point_value = PolygonArray[i].Split(',');
            curvePoints[i] = new hjmap.XPoint((Convert.ToDouble(point_value[0])), (Convert.ToDouble(point_value[1])));
        }

        int rs = InPolygon(curvePoints, mypoint);
        return rs;
    }
}

判断点是否在多边形内

 　  以上便是我们系统中地图订餐部分的内容了，也有做这块的朋友，大家可以交流下。

　　成为一名优秀的程序员！