题目
难度:★★☆☆☆
类型:几何、数学、二维数组
在 N * N 的网格中,我们放置了一些与 x,y,z 三轴对齐的 1 * 1 * 1 立方体。
每个值 v = grid[i][j] 表示 v 个正方体叠放在单元格 (i, j) 上。
现在,我们查看这些立方体在 xy、yz 和 zx 平面上的投影。
投影就像影子,将三维形体映射到一个二维平面上。
在这里,从顶部、前面和侧面看立方体时,我们会看到“影子”。
返回所有三个投影的总面积。
提示
1 <= grid.length = grid[0].length <= 50
0 <= grid[i][j] <= 50
示例
示例 1
输入:[[2]]
输出:5
示例 2
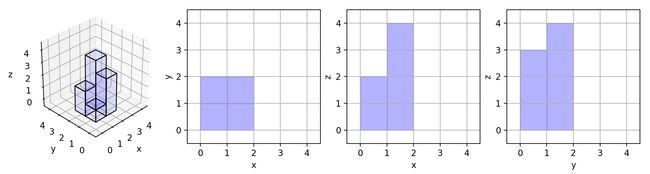
输入:[[1,2],[3,4]]
输出:17
解释:
这里有该形体在三个轴对齐平面上的三个投影(“阴影部分”)。
示例 3
输入:[[1,0],[0,2]]
输出:8
示例 4
输入:[[1,1,1],[1,0,1],[1,1,1]]
输出:14
示例 5
输入:[[2,2,2],[2,1,2],[2,2,2]]
输出:21
解答
每一个三维形体由若干底在同一平面的四棱柱组成,仔细观察一个三维形体的三视图我们可以发现:
俯视图的面积等于四棱柱的个数;
正视图的面积是每一行棱柱的最大高之和;
侧视图的面积是每一列棱柱的最大高之和;
因此,只要按照上述要求求解即可。
class Solution:
def projectionArea(self, grid):
top_view = sum(v > 0 for row in grid for v in row)
front_view = sum(map(max, grid))
side_view = sum(map(max, zip(*grid)))
return sum([top_view, front_view, side_view])
如有疑问或建议,欢迎评论区留言~