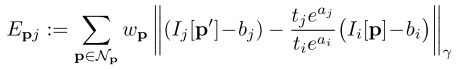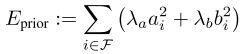光度标定(Photometric Camera Calibration)是DSO(Direct Sparse Odometry)论文中比较特别的一部分。常规的vSLAM不太考虑光度标定的问题。比如基于特征点的vSLAM,由于特征描述一般会有光照不变性,对图像的亮度值并不敏感。而在直接法(direct method)中,由于姿态估计以图像的亮度值为出发点,亮度值的准确度会影响算法的精度和稳定性。因此,作者引入了光度标定的概念,利用精细的相机成像模型,标定成像过程中的光度参数,并用这些参数校正图像亮度值。
由于本人不是光学专业,文中难免有不准确的地方,还望大家不吝赐教。
参考文献
- Direct Sparse Odometry
- A Photometrically Calibrated Benchmark For Monocular Visual Odometry
- Recovering High Dynamic Range Radiance Maps fromPhotographs
- What is the Space of Camera Response Functions?
- Wikipedia
相机成像原理
一般而言,相机测量的是场景中的光的辐射度(radiance)。成像过程如下图[3]。
radiance用来描述物体表面单位面积上的能量分布,和方向有关。
In radiometry, radiance is the radiant flux emitted, reflected, transmitted or received by a surface, per unit solid angle per unit projected area. For example, radiance in direction of the optical axis of a LED is higher than it's radiance at an angle of 15°.
irradiance用来描述物体表面单位面积总的入射能量,和方向无关。比如,用来描述传感器像元的入射光强(来自于不同方向的环境光的累加)。
In radiometry, irradiance is the radiant flux (power) received by a surface per unit area. Irradiance commonly is used referring to power incident on a surface.
下面详细分析一下各个模块的影响。
光学(镜头和光圈)
除了大家熟悉的小孔成像模型和畸变模型,还会有晕影(vignetting)。以下摘自wiki。
光学晕影是由一个或多个透镜的实际尺寸造成的,后方的元件遮蔽了前方的,导致前端透镜离轴的有效入射光减少,结果是光的强度由图像中心向周围逐渐减弱。光学晕影对镜头的开口相当敏感,只要适当的调整光圈就可以消除,通常缩小2至3格就可以完全消除。
也就是说,假如拍摄一个亮度非常均匀的物体,图像中心和边缘的亮度值并不一致。
如果这些因素都没有影响,那么从scene radiance到sensor irradiance的转化是线性的。

快门
快门影响的是曝光时间。自动曝光模式下,不同场景曝光时间并不一样,会导致同一物体在不同场景下的灰度值产生差异。另外还想提到的是全局快门(global shutter)和卷帘快门(rolling shutter)。全局快门保证所有感光元件的曝光起始时间和间隔是一样的,卷帘快门并不能保证。因此文献中一般推荐使用全局快门。
传感器
传感器(CCD/CMOS)将每个像元接收到的光子通过一系列处理转化为亮度值。这里面涉及到光电效应、ADC、DSP等过程。输入的曝光量和输出的亮度值之间的关系称为响应函数(response function)。响应函数一般来说是非线性的,甚至包含人为调整的成分,比如伽马校正、白平衡、色调、饱和度等。为图像进行伽马编码的目的是用来对人类视觉的特性进行补偿,从而根据人类对光线或者黑白的感知,最大化地利用表示黑白的数据位或带宽。人眼对暗部比较敏感,因此一般选择提高暗部的分辨率。这些因素会非线性地修正曝光量,因此作者希望通过光度标定来补偿它们的影响。
论文解析
下面我们来看看作者在DSO中如何排除这些因素的影响。作者采用的数据集中有两个镜头,一个鱼眼一个广角。上一节提到的三个因素都有影响。
- 用函数V来表示光学模块的影响。V是光学模块的固有属性,作者用一个权重矩阵(和图像一样大)来表示其对每个像元的影响。
- 用t来表示曝光时间。相机有开启自动曝光时,每一帧的t都不相同。
- 用函数G来表示响应函数,其值域是离散的(比如0~255)。G是传感器的固有属性。
用B表示不受光学模块影响的sensor irradiance图像,I表示输出的图像,作者提出的成像模型为(参考文献1式(2))
标定响应函数
响应函数有几种常见的参数模型,比如线性、伽马和基函数。而作者用非参数估计的方法来标定。具体而言,在固定场景下,相机在不同曝光时间下,重复拍照得到一系列图像。由于场景不变,B在不同图像中是一样的,图像亮度值的差异来源于曝光时间和响应函数。因此,作者构建了一个能量误差函数,用迭代的方法求解U=G^{-1}。其中待求解变量为B和U。每步迭代中,先用估计的U求解B,然后用更新的B求解U。具体细节参见文献2第2.3.1节。
实验中,作者采集了1000幅不同曝光的图像,其中的5幅见下图。
文献2图3提供了作者标定出的gamma校正曲线。蓝色是有gamma校正的结果,绿色是没有gamma校正的结果。
标定晕影
假设响应函数G已经标定好了。作者通过大量图像数据,迭代估计V的值。具体而言,从不同角度重复拍摄一个 Lambertian surface,得到一系列图像。作者选择了白墙作为Lambertian surface。理想光照下,墙上的每个点在不同角度下的radiance是均匀的,因此B在不同图像中是一样的。作者并不要求白墙的亮度均匀,因此B中每个点的值是不一样的。场景见下图
利用响应函数的逆得到B'=V*B。作者构建了一个能量误差函数,用迭代的方法求解V。其中待求解变量为B和V。每步迭代中,先用估计的V求解B,然后用更新的B求解V。具体细节参见文献2第2.3.2节。
从不同角度拍摄时,白墙上不同位置的三维点相对于镜头的位置是不一样的,晕影的影响也不一样。因此需要将白墙变换到相机坐标系,引入了姿态估计的问题。作者用了一个AR marker来估计姿态。
文献2中,作者采集了700幅图像,其中的4幅见下图。
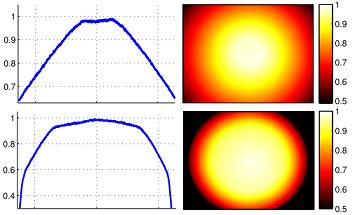
文献2图4给出了两个不同镜头模组的晕影。
有光度标定时的处理
通过标定V和G,就可以反解出B(参考文献1式(3))。使用B去做直接法当然要比I准确地多。当然,场景的亮度在不同视角下有差异,这是无法避免的。
一般情形
对于做过光度标定的相机,我们可以用上面的方法处理。对于一般的相机怎么办呢?作者在估计姿态的同时,还估计图像校正参数,用于粗略去除响应函数的影响。具体做法是加入一个affine brightness transfer function。个人理解,这个affine brightness transfer function其实是线性响应函数的逆函数。(似乎也可看做是一种归一化的方式)
![]()
这个函数可以校正曝光时间(正比于e^{-a_i})和图像亮度基底(b_i)的影响。晕影不太好建模,作者暂时没有考虑。
因此,总的姿态估计的目标函数为
这里的I指的是校正过的亮度值。当没有光度标定时,G=V=t=1,因此I就是输出图像本身。有光度标定时,I=t*B。
作者还加入正则项来平衡有无光度标定的影响。
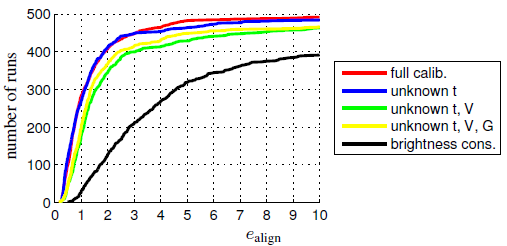
当有光度标定时,a_i和b_i可以设为0,也可以不为0(相当于额外的校正,正则项限制了它们不会很大)。当没有光度标定时,lambda_a和lambda_b均为0,也就是说,a_i和b_i不做任何限制,均作为待求参数参与优化。另外,当lambda_a和lambda_b均为无穷时,a_i和b_i必须为0,因此不会优化图像校正的参数(即参考文献1图14中的brightness constancy)。光度标定参数的影响见参考文献1第4.2小结。
思考:一般情形下,是否可以用伽玛响应函数代替线性响应函数?只需要一个额外的参数就可以模拟非线性的情形。
小结
推荐大家有时间看一下参考文献2。想发自内心地吹一波,Engel他们的工作做得真是太细致了。