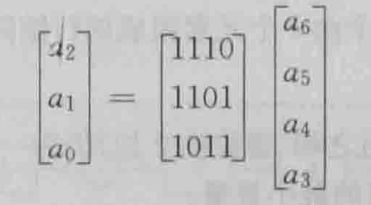通信原理（第七版）-樊昌信-第十一章-差错控制编码-重要知识点

1.基本概念：

　　在信道编码器在信息码元序列中按照一定关系加入一些冗余码元（监督码元），之后，信道译码器通过利用这种关系发现或者纠正可能存在的错码；

1.1 差错控制方式：

　　根据错码的不同分布规律，将信道分为3类：随机、突发、混合信道。

　　　　差错控制方式：

　　（1）ARQ：检错重发；（双向，效率低，但是编译码简单）

　　（2）FEC：前向纠错；（单项，效率高，译码简单）

　　（3）反馈校验：收到后发回给发送端，与原发送码比较，若不同，则有错，重新发；（双向，收发简单，但是效率低）

1.2 系统码：

　　编码后信息码保持不变，监督码在信息码后面（eg：（7,4）汉明码）；

1.3 码重：

　　非“0”码的个数；

1.4 码距：

　　两个码组对应位数字不同的位数，即汉明距；

1.5 最小码距与纠检错能力：

　　1.5.1 最小码距：各个码组之间距离的最小值，决定该编码的纠检错能力；

　　1.5.2 纠检错能力：

　　　　检e各错：d0  >=  e + 1

　　　　纠t个错：d0 >= 2*t + 1

　　　　检e个错，并纠正t个错：d0 >= t + e+ 1 （e > t）

1.6 编码效率：k/n

1.7 冗余度：（n - k）/n

1.8 编码增益：

　　误码率恒定的条件下，采用纠错编码所节省的信噪比；

 

2.奇偶检验码：

2.1 一维奇偶校验码：

　　（1）编码效率：（n - 1）/n

　　（2）解释：加了一个监督位，使得“1”的个数为奇数或者偶数个；

　　（3）检错能力：检测奇数个错码，但是对突发差错漏检概率接近1/2；

2.2 二维奇偶校验码：

　　可能检测偶数个错码（从行或者列看都是偶数个错码检测不出来）；

 

3.线性分组码：

3.1 性质：

　　封闭性：任意两个许用码组之和仍为一个许用码组；

　　最小码距：等于非全0码组中的最小码距；

3.2 汉明码：

　　编码效率最高的线性分组码；

3.2.1 2^r-1 ≥ n = k + r

　　记忆：检错的个数为2^r-1，总位数为n，肯定是检错的个数至少要大于总编码的位数吧，不然都检不完；

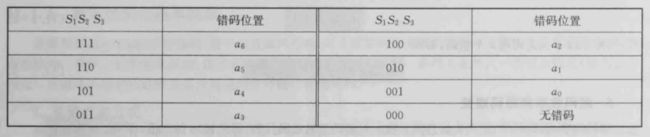
3.2.2 校正子与错码位置的关系：

规律：

（1）000不用说；a0、a1、a2 这三个将1往前走；a3、a4将最后一位固定为1，然后1往前跑；a5讲两个1出现的补全；a6：不用说；

（2）（7,4）汉明码：2³ = 8 

3.2.3 生成监督矩阵：

 令S1、S2、S3 = 0 0 0 认为无错，再将方程两边摩尔加a2、a1、a0得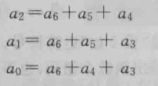：（这个也叫监督方程）

 H为典型监督矩阵；（后面的000是s1s2s3）

3.2.4 生成矩阵：

　　 or  （Q = P^T）

得生成矩阵为：

许用码组为：

 3.2.5 校正子与译码：

　　对于接收码组B，有：B·H^T = S（为0矩阵：无错或者检测不出来错误；为非0矩阵，有错；）

解得错误图样E；中华纠正后的码组：A = B + E

若校正子等于典型监督矩阵的各列，则说明对应的码元传错了；

 

4.补充：

4.1 错码图样表：

an-1   ----->   a0：对应于H^{T；外加一个 无错}

4.2 生成多项式g（x）对应前面k-1位都为0

　　得生成矩阵G（x）（x×到k-1次方）

　　G典型化；

　　G = Ik*Q；

　　之后推到出H；

 

#完结：撒花，撒花；#

　　写这个的主要目的有，梳理知识点，然后还有方便以后的查找，还有当时自己学习时候的有的记忆方法以及为了捡起来容易。中途有很多的是自己笔记拍的，不整齐，但是时间有限，算了吧，这样看吧，有什么不懂欢迎来交流（QQ：1614242015）；

　　以后从事不从事通信自己也不知道，但是通信原理我认为得是得给大学的一个小的交代，希望自己考研复试调剂顺利吧，期待有一个好的结果，努力！