CheeseZH: Stanford University: Machine Learning Ex2:Logistic Regression

1. Sigmoid Function

In Logisttic Regression, the hypothesis is defined as:

where function g is the sigmoid function. The sigmoid function is defined as:

2.Cost function and gradient

The cost function in logistic regression is:

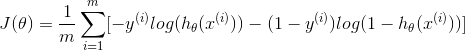
the gradient of the cost is a vector of the same length as θ  where j^th element(for j=0,1,...,n) is defined as follows:

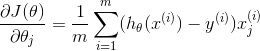
3. Regularized Cost function and gradient

Recall that the regularized cost function in logistic regression is:

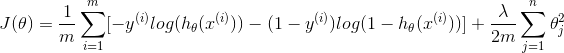
The gradient of the cost function is a vector where the j^th element is defined as follows:

for j=0:

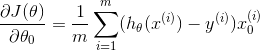
for j>=1:

 

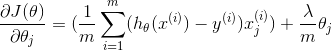
Here are the code files:

ex2_data1.txt

 

34.62365962451697,78.0246928153624,0

30.28671076822607,43.89499752400101,0

35.84740876993872,72.90219802708364,0

60.18259938620976,86.30855209546826,1

79.0327360507101,75.3443764369103,1

45.08327747668339,56.3163717815305,0

61.10666453684766,96.51142588489624,1

75.02474556738889,46.55401354116538,1

76.09878670226257,87.42056971926803,1

84.43281996120035,43.53339331072109,1

95.86155507093572,38.22527805795094,0

75.01365838958247,30.60326323428011,0

82.30705337399482,76.48196330235604,1

69.36458875970939,97.71869196188608,1

39.53833914367223,76.03681085115882,0

53.9710521485623,89.20735013750205,1

69.07014406283025,52.74046973016765,1

67.94685547711617,46.67857410673128,0

70.66150955499435,92.92713789364831,1

76.97878372747498,47.57596364975532,1

67.37202754570876,42.83843832029179,0

89.67677575072079,65.79936592745237,1

50.534788289883,48.85581152764205,0

34.21206097786789,44.20952859866288,0

77.9240914545704,68.9723599933059,1

62.27101367004632,69.95445795447587,1

80.1901807509566,44.82162893218353,1

93.114388797442,38.80067033713209,0

61.83020602312595,50.25610789244621,0

38.78580379679423,64.99568095539578,0

61.379289447425,72.80788731317097,1

85.40451939411645,57.05198397627122,1

52.10797973193984,63.12762376881715,0

52.04540476831827,69.43286012045222,1

40.23689373545111,71.16774802184875,0

54.63510555424817,52.21388588061123,0

33.91550010906887,98.86943574220611,0

64.17698887494485,80.90806058670817,1

74.78925295941542,41.57341522824434,0

34.1836400264419,75.2377203360134,0

83.90239366249155,56.30804621605327,1

51.54772026906181,46.85629026349976,0

94.44336776917852,65.56892160559052,1

82.36875375713919,40.61825515970618,0

51.04775177128865,45.82270145776001,0

62.22267576120188,52.06099194836679,0

77.19303492601364,70.45820000180959,1

97.77159928000232,86.7278223300282,1

62.07306379667647,96.76882412413983,1

91.56497449807442,88.69629254546599,1

79.94481794066932,74.16311935043758,1

99.2725269292572,60.99903099844988,1

90.54671411399852,43.39060180650027,1

34.52451385320009,60.39634245837173,0

50.2864961189907,49.80453881323059,0

49.58667721632031,59.80895099453265,0

97.64563396007767,68.86157272420604,1

32.57720016809309,95.59854761387875,0

74.24869136721598,69.82457122657193,1

71.79646205863379,78.45356224515052,1

75.3956114656803,85.75993667331619,1

35.28611281526193,47.02051394723416,0

56.25381749711624,39.26147251058019,0

30.05882244669796,49.59297386723685,0

44.66826172480893,66.45008614558913,0

66.56089447242954,41.09209807936973,0

40.45755098375164,97.53518548909936,1

49.07256321908844,51.88321182073966,0

80.27957401466998,92.11606081344084,1

66.74671856944039,60.99139402740988,1

32.72283304060323,43.30717306430063,0

64.0393204150601,78.03168802018232,1

72.34649422579923,96.22759296761404,1

60.45788573918959,73.09499809758037,1

58.84095621726802,75.85844831279042,1

99.82785779692128,72.36925193383885,1

47.26426910848174,88.47586499559782,1

50.45815980285988,75.80985952982456,1

60.45555629271532,42.50840943572217,0

82.22666157785568,42.71987853716458,0

88.9138964166533,69.80378889835472,1

94.83450672430196,45.69430680250754,1

67.31925746917527,66.58935317747915,1

57.23870631569862,59.51428198012956,1

80.36675600171273,90.96014789746954,1

68.46852178591112,85.59430710452014,1

42.0754545384731,78.84478600148043,0

75.47770200533905,90.42453899753964,1

78.63542434898018,96.64742716885644,1

52.34800398794107,60.76950525602592,0

94.09433112516793,77.15910509073893,1

90.44855097096364,87.50879176484702,1

55.48216114069585,35.57070347228866,0

74.49269241843041,84.84513684930135,1

89.84580670720979,45.35828361091658,1

83.48916274498238,48.38028579728175,1

42.2617008099817,87.10385094025457,1

99.31500880510394,68.77540947206617,1

55.34001756003703,64.9319380069486,1

74.77589300092767,89.52981289513276,1

View Code

 

ex2.m

  1 %% Machine Learning Online Class - Exercise 2: Logistic Regression

  2 %

  3 %  Instructions

  4 %  ------------

  5 % 

  6 %  This file contains code that helps you get started on the logistic

  7 %  regression exercise. You will need to complete the following functions 

  8 %  in this exericse:

  9 %

 10 %     sigmoid.m

 11 %     costFunction.m

 12 %     predict.m

 13 %     costFunctionReg.m

 14 %

 15 %  For this exercise, you will not need to change any code in this file,

 16 %  or any other files other than those mentioned above.

 17 %

 18 

 19 %% Initialization

 20 clear ; close all; clc

 21 

 22 %% Load Data

 23 %  The first two columns contains the exam scores and the third column

 24 %  contains the label.

 25 

 26 data = load('ex2data1.txt');

 27 X = data(:, [1, 2]); y = data(:, 3);

 28 

 29 %% ==================== Part 1: Plotting ====================

 30 %  We start the exercise by first plotting the data to understand the 

 31 %  the problem we are working with.

 32 

 33 fprintf(['Plotting data with + indicating (y = 1) examples and o ' ...

 34          'indicating (y = 0) examples.\n']);

 35 

 36 plotData(X, y);

 37 

 38 % Put some labels 

 39 hold on;

 40 % Labels and Legend

 41 xlabel('Exam 1 score')

 42 ylabel('Exam 2 score')

 43 

 44 % Specified in plot order

 45 legend('Admitted', 'Not admitted')

 46 hold off;

 47 

 48 fprintf('\nProgram paused. Press enter to continue.\n');

 49 pause;

 50 

 51 

 52 %% ============ Part 2: Compute Cost and Gradient ============

 53 %  In this part of the exercise, you will implement the cost and gradient

 54 %  for logistic regression. You neeed to complete the code in 

 55 %  costFunction.m

 56 

 57 %  Setup the data matrix appropriately, and add ones for the intercept term

 58 [m, n] = size(X);

 59 

 60 % Add intercept term to x and X_test

 61 X = [ones(m, 1) X];

 62 

 63 % Initialize fitting parameters

 64 initial_theta = zeros(n + 1, 1);

 65 

 66 % Compute and display initial cost and gradient

 67 [cost, grad] = costFunction(initial_theta, X, y);

 68 

 69 fprintf('Cost at initial theta (zeros): %f\n', cost);

 70 fprintf('Gradient at initial theta (zeros): \n');

 71 fprintf(' %f \n', grad);

 72 

 73 fprintf('\nProgram paused. Press enter to continue.\n');

 74 pause;

 75 

 76 

 77 %% ============= Part 3: Optimizing using fminunc  =============

 78 %  In this exercise, you will use a built-in function (fminunc) to find the

 79 %  optimal parameters theta.

 80 

 81 %  Set options for fminunc

 82 options = optimset('GradObj', 'on', 'MaxIter', 400);

 83 

 84 %  Run fminunc to obtain the optimal theta

 85 %  This function will return theta and the cost 

 86 [theta, cost] = ...

 87     fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);

 88 

 89 % Print theta to screen

 90 fprintf('Cost at theta found by fminunc: %f\n', cost);

 91 fprintf('theta: \n');

 92 fprintf(' %f \n', theta);

 93 

 94 % Plot Boundary

 95 plotDecisionBoundary(theta, X, y);

 96 

 97 % Put some labels 

 98 hold on;

 99 % Labels and Legend

100 xlabel('Exam 1 score')

101 ylabel('Exam 2 score')

102 

103 % Specified in plot order

104 legend('Admitted', 'Not admitted')

105 hold off;

106 

107 fprintf('\nProgram paused. Press enter to continue.\n');

108 pause;

109 

110 %% ============== Part 4: Predict and Accuracies ==============

111 %  After learning the parameters, you'll like to use it to predict the outcomes

112 %  on unseen data. In this part, you will use the logistic regression model

113 %  to predict the probability that a student with score 45 on exam 1 and 

114 %  score 85 on exam 2 will be admitted.

115 %

116 %  Furthermore, you will compute the training and test set accuracies of 

117 %  our model.

118 %

119 %  Your task is to complete the code in predict.m

120 

121 %  Predict probability for a student with score 45 on exam 1 

122 %  and score 85 on exam 2 

123 

124 prob = sigmoid([1 45 85] * theta);

125 fprintf(['For a student with scores 45 and 85, we predict an admission ' ...

126          'probability of %f\n\n'], prob);

127 

128 % Compute accuracy on our training set

129 p = predict(theta, X);

130 

131 fprintf('Train Accuracy: %f\n', mean(double(p == y)) * 100);

132 

133 fprintf('\nProgram paused. Press enter to continue.\n');

134 pause;

View Code

sigmoid.m

 1 function g = sigmoid(z)

 2 %SIGMOID Compute sigmoid functoon

 3 %   J = SIGMOID(z) computes the sigmoid of z.

 4 

 5 % You need to return the following variables correctly 

 6 g = zeros(size(z));

 7 

 8 % ====================== YOUR CODE HERE ======================

 9 % Instructions: Compute the sigmoid of each value of z (z can be a matrix,

10 %               vector or scalar).

11 

12 

13 g = 1./(1+exp(-z));

14 

15 

16 % =============================================================

17 

18 end

View Code

costFunction.m

 1 function [J, grad] = costFunction(theta, X, y)

 2 %COSTFUNCTION Compute cost and gradient for logistic regression

 3 %   J = COSTFUNCTION(theta, X, y) computes the cost of using theta as the

 4 %   parameter for logistic regression and the gradient of the cost

 5 %   w.r.t. to the parameters.

 6 

 7 % Initialize some useful values

 8 m = length(y); % number of training examples

 9 

10 % You need to return the following variables correctly 

11 J = 0;

12 grad = zeros(size(theta));

13 

14 % ====================== YOUR CODE HERE ======================

15 % Instructions: Compute the cost of a particular choice of theta.

16 %               You should set J to the cost.

17 %               Compute the partial derivatives and set grad to the partial

18 %               derivatives of the cost w.r.t. each parameter in theta

19 %

20 % Note: grad should have the same dimensions as theta

21 %

22 hx = sigmoid(X*theta);  % m x 1

23 J = -1/m*(y'*log(hx)+((1-y)'*log(1-hx)));

24 grad = 1/m*X'*(hx-y);

25 

26 

27 

28 

29 

30 

31 % =============================================================

32 

33 end

View Code

predict.m

 1 function p = predict(theta, X)

 2 %PREDICT Predict whether the label is 0 or 1 using learned logistic 

 3 %regression parameters theta

 4 %   p = PREDICT(theta, X) computes the predictions for X using a 

 5 %   threshold at 0.5 (i.e., if sigmoid(theta'*x) >= 0.5, predict 1)

 6 

 7 m = size(X, 1); % Number of training examples

 8 

 9 % You need to return the following variables correctly

10 p = zeros(m, 1);

11 

12 % ====================== YOUR CODE HERE ======================

13 % Instructions: Complete the following code to make predictions using

14 %               your learned logistic regression parameters. 

15 %               You should set p to a vector of 0's and 1's

16 %

17 

18 p = sigmoid(X*theta)>=0.5;

19 

20 

21 

22 

23 % =========================================================================

24 

25 

26 end

View Code

costFunctionReg.m

 1 function [J, grad] = costFunctionReg(theta, X, y, lambda)

 2 %COSTFUNCTIONREG Compute cost and gradient for logistic regression with regularization

 3 %   J = COSTFUNCTIONREG(theta, X, y, lambda) computes the cost of using

 4 %   theta as the parameter for regularized logistic regression and the

 5 %   gradient of the cost w.r.t. to the parameters. 

 6 

 7 % Initialize some useful values

 8 m = length(y); % number of training examples

 9 

10 % You need to return the following variables correctly 

11 J = 0;

12 grad = zeros(size(theta));

13 

14 % ====================== YOUR CODE HERE ======================

15 % Instructions: Compute the cost of a particular choice of theta.

16 %               You should set J to the cost.

17 %               Compute the partial derivatives and set grad to the partial

18 %               derivatives of the cost w.r.t. each parameter in theta

19 hx = sigmoid(X*theta);

20 reg = lambda/(2*m)*sum(theta(2:size(theta),:).^2);

21 J = -1/m*(y'*log(hx)+(1-y)'*log(1-hx)) + reg;

22 theta(1) = 0;

23 grad = 1/m*X'*(hx-y)+lambda/m*theta;

24 

25 

26 % =============================================================

27 

28 end

View Code