最短路径之Dijkstra算法

【最短路径】之Dijkstra算法

---

最短路径问题是图论研究中的一个经典算法问题，旨在寻找图（由结点和路径组成的）中两结点之间的最短路径。算法具体的形式包括：

• 确定起点的最短路径问题 - 即已知起始结点，求最短路径的问题。适合使用Dijkstra算法。
• 确定终点的最短路径问题 - 与确定起点的问题相反，该问题是已知终结结点，求最短路径的问题。在无向图中该问题与确定起点的问题完全等同，在有向图中该问题等同于把所有路径方向反转的确定起点的问题。
• 确定起点终点的最短路径问题 - 即已知起点和终点，求两结点之间的最短路径。
• 全局最短路径问题 - 求图中所有的最短路径。适合使用Floyd-Warshall算法。

用于解决最短路径问题的算法被称做“最短路径算法”，有时被简称作“路径算法”。最常用的路径算法有：

• Dijkstra算法
• Bellman-Ford算法
• SPFA算法（Bellman-Ford算法的改进版本）
• Floyd-Warshall算法
• 深度或广度优先搜索算法（解决单源最短路径）

应用实例——计算机网络传输的问题：怎样找到一种最经济的方式，从一台计算机向网上所有其它计算机发送一条消息。

---

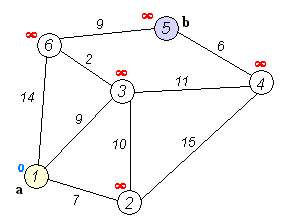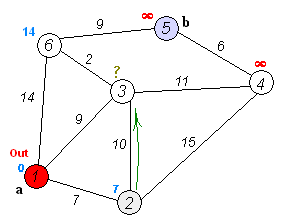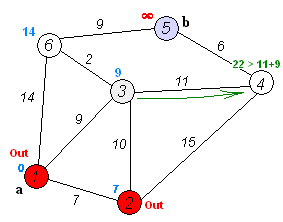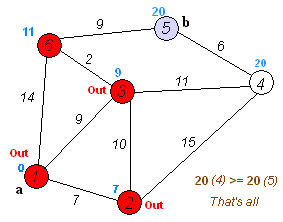
Dijkstra算法基本思想：每次找到离源点（如1号结点）最近的一个顶点，然后以该顶点为中心进行扩展，最终得到源点到其余所有点的最短路径。

基本步骤：

1，设置标记数组book[]：将所有的顶点分为两部分,已知最短路径的顶点集合P和未知最短路径的顶点集合Q，很显然最开始集合P只有源点一个顶点。book[i]为1表示在集合P中；

2，设置最短路径数组dis[]并不断更新：初始状态下，令dis[i] = edge[s]i，很显然此时dst[s]=0，book[s]=1。此时，在集合\(Q\)中可选择一个离源点\(s\)最近的顶点\(u\)加入到\(P\)中。并依据以\(u\)为新的中心点，对每一条边进行松弛操作(松弛是指由结点\(s->j\)的途中可以经过点u，并令\(dst[j]=min{dst[j], dst[u]+edge[u][j]})\)，并令book[u]=1;
3，在集合Q中再次选择一个离源点s最近的顶点v加入到P中。并依据v为新的中心点，对每一条边进行松弛操作(即\(dst[j]=min{dst[j], dst[v]+edge[v][j]})\),并令book[v]=1;
4，重复3，直至集合Q为空。

图示：

参考源程序：

以下是该算法不使用堆优化的一个C++实现

#include
using namespace std;

int main()
{
	int map[10][10], dis[10], book[10] = { 0 };
	int inf = 999999, t1, t2, t3, n, m, min = inf;

	cin >> n >> m;
	//初始化map地图数组
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= n; ++j)
			if (i == j)map[i][j] = 0;
			else map[i][j] = inf;

	for (int i = 1; i <= m; ++i)
	{
		cin >> t1 >> t2 >> t3;
		map[t1][t2] = t3;
	}

	for (int i = 1; i <= n; ++i)
		dis[i] = map[1][i];
	book[1] = 1;

	//Dijkstra算法核心
	int u;
	for (int i = 1; i <= n-1; ++i)
	{
		min = inf;
		//找到离1号顶点最近的顶点，u存储
		for (int j = 1; j <= n; ++j)
		{
			if (book[j] == 0 && dis[j] < min)
			{
				min = dis[j];
				u = j;
			}
		}
		book[u] = 1;
		for (int v = 1; v <= n; ++v)
		{
			if (map[u][v] < inf)
			{
				if (dis[v] > dis[u] + map[u][v])
					dis[v] = dis[u] + map[u][v];
			}
		}
	}
	

	for (int i = 1; i <= n; ++i)
		cout << dis[i] << " ";
	cout << endl;
	return 0;
}