- 1.分治 (超时)
递归、分治、动态规划本质上都是去找重复子问题,那么这道题的重复子问题或者说是重复性是什么呢?
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
我们拿第二层来说吧:
从第一层到第二层就是:2 + min(3及后面数的和,4及后面数的和),到第三层也是这样的,那么现在我们就不要人肉递归了,下面的方程就是我们找到的重复性,怎么感觉和数学里面推导公式一样,好像就是推导公式哈
int minimumTotal(int** triangle, int triangleSize, int* triangleColSize){
int ret;
ret = recursion(triangle,triangleSize,triangleColSize,0,0);
return ret;
}
int recursion(int** triangle,int triangleSize,int* triangleColSize,int level,int column) {
// terminator
if (level == triangleSize-1) {
return triangle[level][column];
}
//process current login and drill down
int left = recursion(triangle,triangleSize,triangleColSize,level+1,column);
int right = recursion(triangle,triangleSize,triangleColSize,level+1,column+1);
int minNum = left < right ? left : right;
return minNum + triangle[level][column];
}
- 2.添加记忆化数组 ac
重复计算的字在哪,一开始的时候我想不清楚,就手动在纸上画了一下,下面是我在电脑上画的:
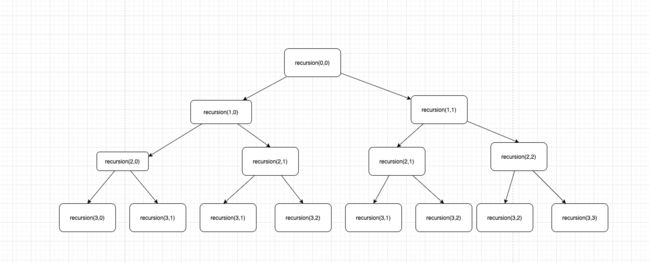
你会发现里面很多是重复计算的,所以我们可以加一个记忆化数组来避免这些重复计算
int minimumTotal(int** triangle, int triangleSize, int* triangleColSize){
if (triangleSize <= 0) {
return 0;
}
int ret;
int **memo = calloc(triangleSize,sizeof(int *));
int i;
for (i = 0;i < triangleSize;i++) {
memo[i] = calloc(triangleSize,sizeof(int));
}
ret = recursion(triangle,triangleSize,triangleColSize,0,0,memo);
return ret;
}
int recursion(int** triangle,int triangleSize,int* triangleColSize,int level,int column,int **memo) {
if (memo[level][column] != 0) {
return memo[level][column];
}
// terminator
if (level == triangleSize-1) {
return triangle[level][column];
}
int left = recursion(triangle,triangleSize,triangleColSize,level+1,column,memo);
int right = recursion(triangle,triangleSize,triangleColSize,level+1,column+1,memo);
int minNum = left < right ? left : right;
if (memo[level][column] == 0) {
memo[level][column] = minNum + triangle[level][column];
}
return memo[level][column];
}
- 3.动态规划
首先我们分析找到动态方程:
a.找重复性:
Problem(i,j) = min(subproblem(i+1,j),subprobelm(i+1,j+1) + a[i,j];
b. 定义状态数组,一维状态还是二维状态
c. DP方程:
F[i,j] = min(F[i+1,j],F[i+1,j+1]) + a[i,j];
代码如下,这道题还是比较有意思的,递推的时候先初始化最下面的,然后从下向上递推,那么可以从上往下递推么,我想了下,不是很方便,我们递推方程里面写的是[i,j] 它需要的是[i+1,j] 和 [i+1,j+1] 的值,从上往下的话好像是变成递推了,不知道我想的对不对,如果不对请指出哈,所以我们还是从下往上来遍历
int minimumTotal(int** triangle, int triangleSize, int* triangleColSize){
int i,j;
int **dp;
dp = malloc(triangleSize * sizeof(int *));
for (i = 0; i < triangleSize;i++) {
dp[i] = malloc(sizeof(int) * triangleSize);
}
// 初始化最下面一排的dp数组
for (i = 0;i < triangleColSize[triangleSize-1];i++) {
dp[triangleSize-1][i] = triangle[triangleSize-1][i];
}
for (i = triangleSize-2;i>=0;i--) {
for (j = 0; j < triangleColSize[i];j++) {
int minNum;
minNum = dp[i+1][j] < dp[i+1][j+1] ? dp[i+1][j] : dp[i+1][j+1];
dp[i][j] = minNum + triangle[i][j];
}
}
return dp[0][0];
}
- 4.动态规划,我们可不可以一维数组替换二维数组存储呢,可以的哈,代码如下
int minimumTotal(int** triangle, int triangleSize, int* triangleColSize){
int i,j;
int *dp;
dp = malloc(triangleSize * sizeof(int));
// 初始化最下面一排的dp数组
for (i = 0;i < triangleColSize[triangleSize-1];i++) {
dp[i] = triangle[triangleSize-1][i];
}
for (i = triangleSize-2;i>=0;i--) {
for (j = 0; j < triangleColSize[i];j++) {
int minNum;
minNum = dp[j] < dp[j+1] ? dp[j] : dp[j+1];
dp[j] = minNum + triangle[i][j];
}
}
return dp[0];
}
5.总结:
学习代码和解决问题的过程都是层层推进,一点点的积累的,中间是没有银弹的,只有我们一点点的付出和积累。这道题也一样,从分治超时,然后到记忆话数组存储解决超时的问题,再然后到二维数组的动态规划,最后到一维数组动态规划,都是一步步改进来的,所以无论生活还是工作,学习中都是没有捷径的。