一、前言
这几天在研究MySQL相关的内容,而MySQL中比较重要的一个内容就是索引。对MySQL索引有了解的应该都知道,B+树是MySQL索引实现的一个主要的数据结构。今天这篇博客就来简单介绍一下B树、B+树以及MySQL索引使用这种数据结构实现的原因。
二、正文
2.1 B树
关于B树的操作细节我这里就不详细介绍了,这里主要介绍一下B树的结构,让大家对B树有一个大致的了解。
这里首先要纠正一个问题,网上大量文章将B树称为B-(减)树,但其实这是一种错误的叫法。会这么叫是因为B树的英文名称为“B-Tree”,错误的翻译导致这种错误的叫法逐渐传开。但实际上这里的“-”是杠,而不是减,由于存在B+树,所以大家都觉得存在一个B-(减)树是很正常的,但实际上,B+树的英文完整写法应该是B+-Tree,“+”是加,但“-”是杠。除此之外,甚至有人认为B树就是二叉搜索树(Binary Search Tree,简称BST),这就错的更加离谱了。
B树是一棵多路平衡查找树,相信很多人都了解过二叉搜索树,而B树和二叉搜索树类似,只是B树的每一个节点可以有超过两个子节点。而B树中,每一个节点具体可以有几个子节点,这与这棵B树的阶有关,而树的阶一般用字母m表示。抛开B树的维护操作不谈,B树可以简单理解为一棵m叉搜索树。
我们定义,一个树中,每个节点允许的子节点的最大数量,就称为这个数的阶,一般用字母m表示。例如:假设一棵5阶的B数,则B数上的每一个节点,最多只能有5个子节点。除此之外需要注意,B树的阶m > 2。
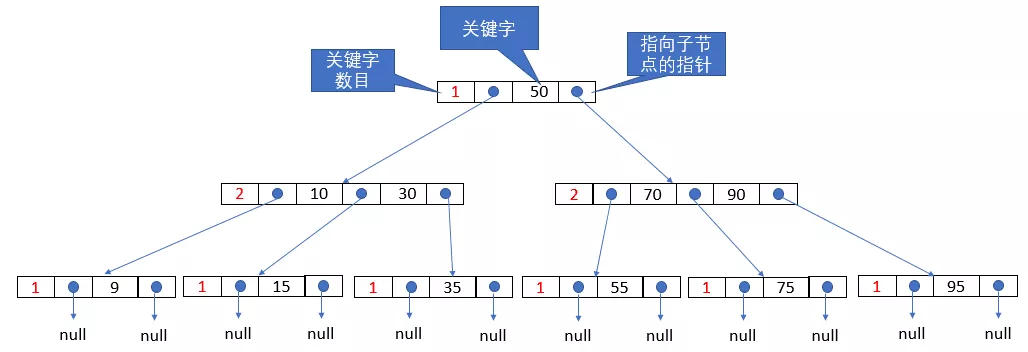
下面我们直接通过一张图来了解B树的结构:
上面这张图就是一棵标准的B树,他的每一个节点中可能存有多个值(每个节点记录了值的个数,也就是上图中的红色数字),以及多个指向子节点的指针,而值的个数 = 指针的个数 - 1 = m - 1。比如说上图中,根节点存有一个值50(图中称为关键字),而根节点的左子节点存有两个值,即10和30。而由于根节点只有一个值,所以他有两个指向子节点的指针,从上图可以看出,这两个指针分别位于值的两边。我们之前说过,B树可以近似的认为是一棵m叉搜索树,所以上图中,根节点的左子树中的所有值都小于根节点的值50,而右边子树中所有节点的值大于根节点的值50。
根节点只有一个值,以及两个子节点,和二叉树类似,所以以它举例不够典型,我们现在以根节点的左子节点再次举例。根节点的左子节点中存有两个值,即10和30,且他有3个指向子节点的指针。在每一个节点中,多个值是排好序的,比如上图中是从小到大排序,于是10在30的左边。对于10左边这个指针指向的子树,包含的值都小于10;而位于10和30之间的指针指向的子树,包含的值一定时10到30之间;而30右边的指针,指向的子树的子节点一定是大于30。
我们现在以一个例子来说明B树查找的过程,假设上图中,我们想要搜索值35,于是需要经历以下步骤:
- 用
35与根节点中的值比较,根节点中只有一个50,35<50,于是向根节点的左子节点搜索; - 根节点的左子节点中的第一个值是
10,35>10,于是判断下一个值,下一个值为30,35>30,继续判断下一个值,但是此节点中没有下一个值了,于是向35右边的这个指针指向的子节点查找,也就是第三个叶子节点; - 到了叶子节点后,发现其中只有一个值,就是
35,于是查找成功;
以上就是在B树中查找一个值的过程。
2.2 为什么需要B树?
在B树的每一个节点中,都不止存储一个值,具体存储的值的个数依赖于B树的阶。而我们在查找一个值的过程中,需要对当前所在的节点包含的所有值进行一个遍历,以此来确定当前查找的值是否在当前节点中。这也就意味着,相比于二叉搜索树,平衡二叉树,红黑树等数据结构,B树查找一个值需要比较更多的次数。假设一棵B树的阶是100,那也就意味着在最坏情况下,我们在每一个访问到的节点中,都需要比较100次,而前面提到的三种数据结构比较的次数不会超过树的深度,也就是只需要少量的比较次数。既然B树相比较于它们需要比较更多的次数才能找到相应的值,那为什么还要B树呢?这取决于实际的应用场景。
说到B树,大部分首先想到的就是数据库的索引,MySQL中使用的索引主要为BTree索引(实际是B+树实现的,这个后面再谈)。从上面的B树结构我们可以看到,B树中使用大量的指针维护节点之间的关系,这也就意味着B树在物理存储上并不是连续的。单个节点中的数据是连续存储,但是多个节点之间一般都是单独存储,然后通过指针相互引用。在实际的存储中,BTree索引一般被存放在磁盘中,然后只有需要使用时,才将使用到的部分节点加载进内存,进行比较判断。
为什么不一次性将BTree索引全部加载进内存?因为在实际生产中,索引往往需要维护百万甚至千万行数据,这就导致索引本身占据大量的内存,再加上我们使用的常常不止一个索引,再加上内存中需要运行其他程序,所以将索引一次性加载进内存是不现实的事情。只有当前需要使用的部分才被加载进内存,而不使用的部分则留在磁盘或者从内存中移除。
而上面这种使用到才进行加载的方式有一个什么问题?我们每次需要查找树中的一个节点,都需要进行一次磁盘IO,将这个节点从磁盘中加载进内存。而对于B树或者说之前提到的平衡二叉树等数据结构,最多需要访问的节点的个数,实际上就是树的深度(想想搜索一个值的过程就能明白)。对于B树来说,他每一个节点可以存储多个值,而平衡二叉树等二叉结构,每一个节点只存储一个值,这也就意味着在值的个数相等的情况下,B树的深度小于二叉树的深度。这也就意味着以B树作为索引,可以进行更少次数的磁盘IO。
对于一棵含有n个元素的树,二叉搜索树的深度在n-log2(n)之间,而平衡二叉树的深度是log2(n),红黑树与平衡二叉树类似,平均深度也是log2(n)。然而,B树设计了一种高效简单的维护操作,使B树的深度维持在约log(ceil(m/2))(n)~logm(n)之间,大大降低树高(ceil是向上取整函数,例如5/2 = 3)。
这里面临一个什么问题?磁盘的速度,相对于内存来说非常的缓慢,磁盘查找的速度比内存查找慢100000倍左右。也就是说,从磁盘中找到1个数据所花费的时间,可以从内存中查找100000个数据。这也就意味着我们在使用索引查找数据的过程中,时间主要是花费在了磁盘IO上,而不是数据的比较上。所以,我们希望尽可能少地进行磁盘IO。而B树作为索引,由于树的深度较小,相比于那些二叉树,可以进行更少的磁盘IO,这就是B树最大的优势。
二叉树中,一个节点一般只存储一个元素,而在将磁盘的数据加载进内存中时,实际上是按页进行加载的,页是每次从磁盘加载进内存的数据的最小单位,一般为4K。这也就意味着我们使用这些二叉树的数据结构时,加载一个节点所在的页进入内存时,这个页中有大量内存都是浪费的。而B树中每一个节点可以存储多个数据,于是我们可以通过修改B树的阶,让他的每一个节点大致占用一个页(4K)的大小,以此最大限度的减少B树的深度,提高内存利用率。
2.3 B树存在的问题
(1)难以存储具体数据
我们上面在介绍B树的过程中,对于B树中存储的元素,都是用“值”这个字来说明,但是在上面那张图中可以看到,图中写的是关键字,这是因为我们在实际使用中,需要存储的是key-value型数据。比如说作为数据库索引,我们需要通过索引值进行查找,索引值就是key,但是我们真正需要的是索引值对应的数据行,也就是value。
有一个比较简单的解决方案,我们可以在B树的节点中直接存储key和value,这样在通过key找到元素是,可以直接取出value。但是,这会导致另外一个问题。我们上面说过,B树的一个节点,其大小一般被限制在一个磁盘页的大小(4K),如果我们在一个节点中既存key,又存value,就会导致一个节点中能够存储的元素数量减少,value越大,能够存储的元素就越少,于是树的深度就会增加,违背了我们使用B树减少磁盘IO的目的,所以这种方法并不可取。当然,其实也可以让value保存数据的地址,但是可能是需要综合考虑下面这个问题,所有没有这样做。
(2)B树不适合用来处理范围查询
在数据库中,进行范围查找的频率非常的高,比如查找员工工资在1000-2000中的全部员工这种类型的查询。但是,B树并不适合用来进行这种范围查找,因为在B树中,每一个节点都用来存储数据,它们之间并不是线性结构,不方便进行范围查询。想要在B树中进行范围查询,可以先找到范围的上界和下界,在通过DFS(或者BFS),遍历包含下界到上界中的所有节点,但这并不方便。
B+树正是针对以上两个问题,而对B树做了一些修改而得来。
2.4 B+树
B+树相对于B树主要做了如下的修改:
- B+树中的每一个非叶子节点并不存储值
value,只存储键key,而具体的value全部存放在子节点中,这也就意味着每次查找需要访问的节点数量都是固定的,都需要向下查找到子节点; - 每一个子节点都有一个指向下一个子节点的指针,所有的子节点相互串联,组成一个线性的结构;
- 对于一个
m阶的B+树,每一个节点最多只有m个子节点,同时存储m个key(对于m阶的B树,只有m-1个key); - 每一个子节点中最小(或最大)的
key,也包含在父节点中(这个通过下面的例子理解);
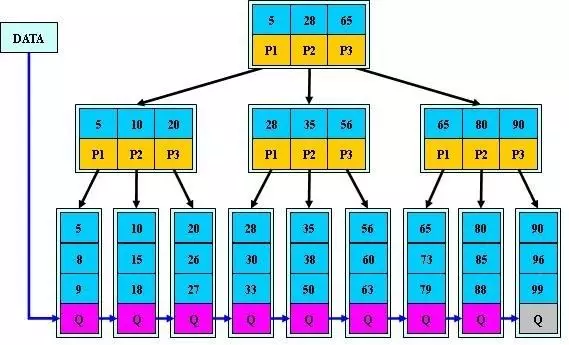
下面我们通过一张图来看看B+树的结构:
上图中,就是一棵B+树。根节点存储了3个key,key值分别是5,28,65,且是按照从小到达的顺序存储。同时根节点包含3个指针,指向自己的3个子节点。第一个子节点中最小的key是5,就是根节点中最小的key,而这个节点中所有的key,大小都是在根节点的第一个key(5)到第二个key(28)之间(不包含28);第二个子节点中最小的key是28,也就是根节点中的第二个key,在这个子节点中所有的key,大小都在根节点第二个key(28)到第三个key(65)之间;第三个子节点同理,它包含根节点的第三个key(65),同时其中所有的key都>=65。再往下的子节点也是同理。
而根据上图我们可以看到,在最下层的叶子节点中,存储了全部的key值(尽管有些key已经在上层节点出现过),同时不仅存储了key值,还存储了这些key值对应的value。除此之外,每一个叶子节点都包含一个指针,指向下一个叶子节点。这些叶子节点相互串联,组成了一个key值从小到大排好序的线性结构。
这样处理有什么好处呢?好处就是我们在树中存储了value,但是由于value存储在叶子节点中,所以对于作为索引的非叶子节点来说,并没有增加它们的大小,从而并没有导致树的高度增加。除此之外,由于value都存储在叶子节点中,并且叶子节点相互串联,所以非常方便进行范围查询。比如说上图,我们要查找key为26-60对应的数据,那我们首先查找26所在的叶子节点,发现它在第三个叶子节点,于是我们将第三个叶子节点读入内存,然后发现并不包含全部数据,于是通过指针找到第四个叶子节点,将第四个叶子节点读入内存,还不包含全部,于是将第五个叶子节点也读入,这时就包含全部数据了。
2.5 InnoDB和MyISAM中索引的实现
在MySQL5.1之前,MySQL的默认存储引擎是MyISAM,而在这之后改为了InnoDB。这两个存储引擎中,都使用了B+Tree实现索引,但是实现的方式有所区别。
(1)InnoDB中的聚簇索引
什么是聚簇索引,就是指索引与数据库表中的数据存储在一起。InnoDB使用B+树实现聚簇索引,而数据库表中的数据行,实际上就是存储在B+树的叶子节点中,我们上面说的B+树中的key-value,其中的value指的就是具体的一行数据,我们在叶子节点中找到了key,实际上也就得到了key对应的那一行数据。所以严格来讲,聚簇索引不单单是索引,更是数据的一种存储结构。
InnoDB使用表的主键作为key,建立聚簇索引,如果表没有主键,将选择一个唯一的非空索引替代,若也没有,将隐式的定义一个主键用来建立。
(2)MyISAM的非聚簇索引
在MyISAM中,并不使用聚簇索引,也就是说MyISAM中通过B+树实现的索引,并不包含表中具体的数据行,子节点中的value,存储的是这一行数据的地址,也就是说数据和索引分开存储。
三、总结
在MySQL的实际应用中,BTree索引都是通过B+树建立的,而不是B树。而在InnoDB中,使用的是聚簇索引,在B+树的叶子节点中直接存储表中的数据行;而MyISAM没有使用聚簇索引,B+树的叶子节点中,存放的是数据行的地址。
四、参考
- https://mp.weixin.qq.com/s/_lNt8WtePf7lKaLsQzawxQ
- https://mp.weixin.qq.com/s/HNN1CWmeXMOKtOe69lLJgQ