图像局部特征点检测算法综述
研究图像特征检测已经有一段时间了,图像特征检测的方法很多,又加上各种算法的变形,所以难以在短时间内全面的了解,只是对主流的特征检测算法的原理进行了学习。总体来说,图像特征可以包括颜色特征、纹理特等、形状特征以及局部特征点等。其中局部特点具有很好的稳定性,不容易受外界环境的干扰,本篇文章也是对这方面知识的一个总结。
本篇文章现在(2015/1/30)只是以初稿的形式,列出了主体的框架,后面还有许多地方需要增加与修改,例如2013年新出现的基于非线性尺度空间的KAZE特征提取方法以及它的改进AKATE等。在应用方面,后面会增一些具有实际代码的例子,尤其是基于特征点的搜索与运动目标跟踪方面。
1. 局部特征点
图像特征提取是图像分析与图像识别的前提,它是将高维的图像数据进行简化表达最有效的方式,从一幅图像的$M\times N\times3$的数据矩阵中,我们看不出任何信息,所以我们必须根据这些数据提取出图像中的关键信息,一些基本元件以及它们的关系。
局部特征点是图像特征的局部表达,它只能反正图像上具有的局部特殊性,所以它只适合于对图像进行匹配,检索等应用。对于图像理解则不太适合。而后者更关心一些全局特征,如颜色分布,纹理特征,主要物体的形状等。全局特征容易受到环境的干扰,光照,旋转,噪声等不利因素都会影响全局特征。相比而言,局部特征点,往往对应着图像中的一些线条交叉,明暗变化的结构中,受到的干扰也少。
而斑点与角点是两类局部特征点。斑点通常是指与周围有着颜色和灰度差别的区域,如草原上的一棵树或一栋房子。它是一个区域,所以它比角点的噪能力要强,稳定性要好。而角点则是图像中一边物体的拐角或者线条之间的交叉部分。
2. 斑点检测原理与举例
2.1 LoG与DoH
斑点检测的方法主要包括利用高斯拉普拉斯算子检测的方法(LOG),以及利用像素点Hessian矩阵(二阶微分)及其行列式值的方法(DOH)。
LoG的方法已经在斑点检测这入篇文章里作了详细的描述。因为二维高斯函数的拉普拉斯核很像一个斑点,所以可以利用卷积来求出图像中的斑点状的结构。
DoH方法就是利用图像点二阶微分Hessian矩阵:
$$H(L) = \begin{bmatrix}L_{xx}&L_{xy}\\L_{xy}&L_{yy}\end{bmatrix}$$
以及它的行列式的值DoH(Determinant of Hessian):
$$det = \sigma^4(L_{xx}(x,y,\sigma)L_{yy}(x,y,\sigma)-L_{xy}^2(x,y,\sigma))$$
Hessian矩阵行列式的值,同样也反映了图像局部的结构信息。与LoG相比,DoH对图像中的细长结构的斑点有较好的抑制作用。
无论是LoG还是DoH,它们对图像中的斑点进行检测,其步骤都可以分为以下两步:
1)使用不同的$\sigma$生成$\left(\frac{\partial^2g}{\partial x^2}+\frac{\partial^2g}{\partial y^2}\right)$或$\frac{\partial^2g}{\partial x^2},\frac{\partial^2g}{\partial y^2},\frac{\partial^2g}{\partial x\partial y}$模板,并对图像进行卷积运算;
2)在图像的位置空间与尺度空间中搜索LoG与DoH响应的峰值。
2.2 SIFT
详细的算法描述参考:SIFT定位算法关键步骤的说明
2004年,Lowe提高了高效的尺度不变特征变换算法(SIFT),利用原始图像与高斯核的卷积来建立尺度空间,并在高斯差分空间金字塔上提取出尺度不变性的特征点。该算法具有一定的仿射不变性,视角不变性,旋转不变性和光照不变性,所以在图像特征提高方面得到了最广泛的应用。
该算法大概可以归纳为三步:1)高斯差分金字塔的构建;2)特征点的搜索;3)特征描述。
在第一步中,它用组与层的结构构建了一个具有线性关系的金字塔结构,让我们可以在连续的高斯核尺度上查找特征点。它比LoG高明的地方在于,它用一阶高斯差分来近似高斯的拉普拉斯核,大大减少了运算量。
在第二步的特征点搜索中,主要的关键步骤是极值点的插值,因为在离散的空间中,局部极值点可能并不是真正意义上的极值点,真正的极植点可以落在了离散点的缝隙中。所以要对这些缝隙位置进行插值,然后再求极值点的坐标位置。
第二步中另一关键环节是删除边缘效应的点,因为只忽略那些DoG响应不够的点是不够的,DoG的值会受到边缘的影响,那些边缘上的点,虽然不是斑点,但是它的DoG响应也很强。所以我们要把这部分点删除。我们利用横跨边缘的地方,在沿边缘方向与垂直边缘方向表现出极大与极小的主曲率这一特性。所以通过计算特征点处主曲率的比值即可以区分其是否在边缘上。这一点在理解上可以参见Harris角点的求法。
最后一步,即为特征点的特征描述。特征点的方向的求法是需要对特征点邻域内的点的梯度方向进行直方图统计,选取直方图中比重最大的方向为特征点的主方向,还可以选择一个辅方向。在计算特征矢量时,需要对局部图像进行沿主方向旋转,然后再进邻域内的梯度直方图统计(4x4x8)。
2.3 SURF
详细的算法描述参考:1. SURF算法与源码分析、上 2. SURF算法与源码分析、下
2006年,Bay和Ess等人基于SIFT算法的思路,提出了加速鲁棒特征(SURF),该算法主要针对于SIFT算法速度太慢,计算量大的缺点,使用了近似Harr小波方法来提取特征点,这种方法就是基于Hessian行列式(DoH)的斑点特征检测方法。通过在不同的尺度上利用积分图像可以有效地计算出近似Harr小波值,简化了二阶微分模板的构建,搞高了尺度空间的特征检测的效率。
SURF算法在积分图像上使用了盒子滤波器对二阶微分模板进行了简化,从而构建了Hessian矩阵元素值,进而缩短了特征提取的时间,提高了效率。其中SURF算法在每个尺度上对每个像素点进行检测,其近似构建的Hessian矩阵及其行列式的值分另为:
$$H_{approx} =\begin{bmatrix}D_{xx}(\sigma)&D_{xy}(\sigma)\\D_{xy}(\sigma)&D_{yy}(\sigma)\end{bmatrix} $$
$$c(x,y,\sigma) = D_{xx}D_{yy}-(0.9D_{xy})^2$$
其中$D_{xx},D_{xy}$和$D_{yy}$为利用盒子滤波器获得的近似卷积值。如果$c(x,y,\sigma)$大于设置的门限值,则判定该像素点为关键字。然后与SIFT算法近似,在以关键点为中心的$3\times3\times3$像素邻域内进行非极大值抑制,最后通过对斑点特征进行插值运算,完成了SURF特征点的精确定位。
而SURF特征点的描述,则也是充分利用了积分图,用两个方向上的Harr小波模板来计算梯度,然后用一个扇形对邻域内点的梯度方向进行统计,求得特征点的主方向。
3. 角点检测的原理与举例
角点检测的方法也是极多的,其中具有代表性的算法是Harris算法与FAST算法。
这两个算法我都有专门写过博文来描述其算法原理。Harris角点和FAST特征点检测。
3.1 Harris角点特征提取
Harris角点检测是一种基于图像灰度的一阶导数矩阵检测方法。检测器的主要思想是局部自相似性/自相关性,即在某个局部窗口内图像块与在各个方向微小移动后的窗口内图像块的相似性。
在像素点的邻域内,导数矩阵描述了数据信号的变化情况。假设在像素点邻域内任意方向上移动块区域,若强度发生了剧烈变化,则变化处的像素点为角点。定义$2\times2$的Harris矩阵为:
$$A(x) = \sum_{x,y}\omega(x,y)\begin{bmatrix}C_x^2(x)&C_xC_y(x)\\C_xC_y(x)&C_y^2(x) \end{bmatrix}= \begin{bmatrix}a&b\\b&c\end{bmatrix}$$
其中,$C_x$和$C_y$分别为点$\mathbf{x} = (x,y)$在$x$和$y$方向上的强度信息的一阶导数,$\omega(x,y)$为对应位置的权重。通过计算Harris矩阵的角点响应值D来判断是否为角点。其计算公式为:
$$D=detA-m(traceA)^2= (ac-b)^2-m(a+c)^2$$
其中,det和trace为行列式和迹的操作符,$m$是取值为0.04~0.06的常数。当角点响应值大于设置的门限,且为该点邻域内的局部最大值时,则把该点当作角点。
3.2 FAST角点特征提取
基于加速分割测试的FAST算法可以快速地提取出角点特征。该算法判断一个候选点$p$是否为角点,依据的是在一个像素点$p$为圆心,半径为3个像素的离散化Bresenllam圆周上,在给定阈值$t$的条件下,如果在圆周上有$n$个连续的像素灰度值大于$I(p)+t$或小于$I(p)-t$。
针对于上面的定义,我们可以用快速的方法来完成检测,而不用把圆周上的所有点都比较一遍。首先比较上下左右四个点的像素值关系,至少要有3个点的像素灰度值大于$I(p)+t$或小于$I(p)-t$,则$p$为候选点,然后再进一步进行完整的判断。
为了加快算法的检测速度,可以使用机器学习ID3贪心算法来构建决策树。这里需要说明的是,在2010年Elmar和Gregory等人提出了自适应通用加速分割检测(AGAST)算法,通过把FAST算法中ID3决策树改造为二叉树,并能够根据当前处理的图像信息动态且高效地分配决策树,提高了算法的运算速度。
4. 二进制字符串特征描述子
可以注意到在两种角点检测算法里,我们并没有像SIFT或SURF那样提到特征点的描述问题。事实上,特征点一旦检测出来,无论是斑点还是角点描述方法都是一样的,可以选用你认为最有效的特征描述子。
特征描述是实现图像匹配与图像搜索必不可少的步骤。到目前为止,人们研究了各种各样的特征描述子,比较有代表性的就是浮点型特征描述子和二进帽字符串特征描述子。
像SIFT与SURF算法里的,用梯度统计直方图来描述的描述子都属于浮点型特征描述子。但它们计算起来,算法复杂,效率较低,所以后来就出现了许多新型的特征描述算法,如BRIEF。后来很多二进制串描述子ORB,BRISK,FREAK等都是在它上面的基础上的改进。
4.1 BRIEF算法
BRJEF算法的主要思想是:在特征点周围邻域内选取若干个像素点对,通过对这些点对的灰度值比较,将比较的结果组合成一个二进制串字符串用来描述特征点。最后,使用汉明距离来计算在特征描述子是否匹配。
BRIEF算法的详细描述可以参考:BRIEF特征描述子
4.2 BRISK算法
BRISK算法在特征点检测部分没有选用FAST特征点检测,而是选用了稳定性更强的AGAST算法。在特征描述子的构建中,BRISK算法通过利用简单的像素灰度值比较,进而得到一个级联的二进制比特串来描述每个特征点,这一点上原理与BRIEF是一致的。BRISK算法里采用了邻域采样模式,即以特征点为圆心,构建多个不同半径的离散化Bresenham同心圆,然后再每一个同心圆上获得具有相同间距的N个采样点。
由于这种邻域采样模式在采样时会产生图像灰度混叠的影响,所以BRISK算法首先对图像进行了高斯平滑图像。并且使用的高斯函数标准差$\sigma_i$与各自同心圆上点间距成正比。
假设在$\dbinom{N}{2}$个采样点中任意选取一对采样点$(p_i,p_j)$,其平滑后的灰度值分别为$I(p_i,\sigma_i)$和$I(p_j,\sigma_j)$,则两点间的局部梯度为:
$$g(p_i,p_j) = (p_j-p_i)\frac{I(p_j,\sigma_j)-I(p_i,\sigma_i)}{\left\|p_j-p_i\right\|^2}$$
假设把所有采样点对构成的集合记为$\boldsymbol{A}$,则
$$\boldsymbol{A} = \{(p_i,p_j)\in R^2\times R^2 | i < N且j<i且i,j\in N\}$$
那么短距离采样点对构成的集合S以及长距离采样点构成的集合L分别为:
$$S=\{(p_i,p_j)\in A | \left\|p_j-p_i\right\|<\delta_{max}\} \subseteq A$$
$$L=\{(p_i,p_j)\in A | \left\|p_j-p_i\right\|>\delta_{min}\} \subseteq A$$
其中,通常设置距离阈值为$\delta_{max} = 9.75\delta,\delta_{min} = 13.67\delta$,其中$\delta$为特征点的尺度。
由于长距离采样点对含有更多的特征点角度信息,且局部梯度相互抵消,所以可以在集合L中计算出特征点的特征模式方向为:
$$g = \begin{pmatrix}g_x\\g_y\end{pmatrix} = \frac{1}{L}\sum_{(p_i,p_j)\in L}g(p_i,p_j)$$
然后将采样模式围绕特征点旋转角度$\alpha = arctan2(g_y,g_x)$,进而特征描述子具有了旋转不变性。
最后,在旋转后的短距离采样点集合S内,对所有的特征点对$(P_i^{\alpha},p_j^{\alpha})$行像素灰度值比较,最终形成512比特的二进制字符串描述子。
4.3 ORB算法
ORB算法使用FAST进行特征点检测,然后用BREIF进行特征点的特征描述,但是我们知道BRIEF并没有特征点方向的概念,所以ORB在BRIEF基础上引入了方向的计算方法,并在点对的挑选上使用贪婪搜索算法,挑出了一些区分性强的点对用来描述二进制串。ORB算法的详细描述可以参考:ORB特征点检测。
4.4 FREAK算法
Fast Retina KeyPoint,即快速视网膜关键点。
根据视网膜原理进行点对采样,中间密集一些,离中心越远越稀疏。并且由粗到精构建描述子,穷举贪婪搜索找相关性小的。42个感受野,一千对点的组合,找前512个即可。这512个分成4组,前128对相关性更小,可以代表粗的信息,后面越来越精。匹配的时候可以先看前16bytes,即代表精信息的部分,如果距离小于某个阈值,再继续,否则就不用往下看了。
5. 应用之图像匹配
图像匹配的研究目标是精确判断两幅图像之间的相似性。图像之间的相似性的定义又随着不同的应用需求而改变。例如,在物体检索系统中(找出含有亚伯拉罕·林肯的脸的图像),我们认为同一物体的不同图像是相近的。而在物体类别检索系统中(找出含有人脸的图像),我们则认为相同类的物体之间是相近的。
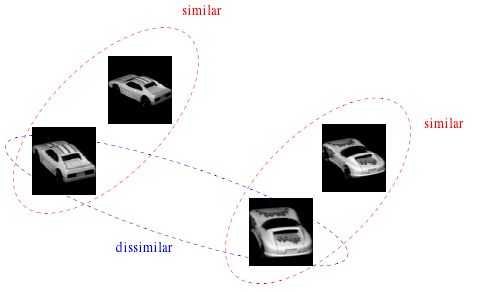
这里局部特征点的应用主要表现在第一种相似性上,也就是说我们需要设计某种图像匹配算法来判断两幅图像是否是对同一物体或场景所成的图像。理想的图像匹配算法应该认为两幅同一物体的图像之间相似度很高,而两幅不同物体的图像之间相似度很低,如下图所示。
由于成像时光照,环境,角度的不一致,我们获取的同一物体的图像是存在差异的,如同上图中的两辆小车的图像一样,角度不同,成像就不同。我们直接利用图像进行比较是无法进行判断小车是否为同一类的。必须进行特征点的提取,再对特征点进行匹配。
图像会存在哪些变换呢?一般来说包括了光照变化与几何变化,光照变化表现是图像上是全局或局部颜色的变化,而几何变化种类就比较多了,可以是平移、旋转、尺度、仿射、投影变换等等。所以我们在研究局部特征点时才要求特征点对这些变化具有稳定性,同时要有很强的独特性,可以让图像与其他类的图像区分性强,即类内距离小而类间距离大。
6. 参考文献
[1] 基于角点的图像特征提取与匹配算法研究,薛金龙,2014.
[2] 基于局部特征的图像匹配与识别,宫明明,2014.
[3] 基于视觉信息的图像特征提取算法研究,戴金波,2014.
[4] 图像局部不变性特征与描述,王永明,王贵锦编著。