Notes About Singular Value Decomposition
A brief summary of SVD:
An original matrix Amn is represented as a muliplication of three matrices:
Amn = UmmSmnVnnT
The columns of U are the orthonormal engenvectors of AAT descendingly ordered by the corresponding eigenvalues, and the columns of V are the orthonormal engenvectors of ATA descendingly ordered by the corresponding eigenvalues. This also suggests that U and V are orthonormal (orthogonal) matrices. A characteristic of the two matrices is that the non-zero eigenvalues of U and V are always the same. S is a diagonal matrix containing the square roots of eigenvalues from U and V in descending order. The diagonal entries in S are the singular values of A, the columns in U are called left singular vectors, and the columns in V are called right singular vectors.
==========================分割线=======================
看完mit的《Introduction To Linear Algebra》(Gilber Strang著)里关于SVD的章节,只能说发觉SVD愈发奇特了,但是很多概念还是不太懂,尤其是作者所说的“四个子空间”。其实看着作者推导的一些公式,自己也跟着推导一番觉得很是爽。但是我只但看了这一章节,未免理解起来过于管中窥豹。虽然自己只是为了做论文,需要弄SVD这个概念,但是一知半解不是什么好习惯,那还是从头看起吧,如果确实觉得不是重要的概念也许可以跳过。习题估计也不需要做,这里就把一些值得记录下的东西记录一下吧。
----
看到序言里讲到列空间,忽然再一次被自己对于线性代数很多基本问题的无知击倒:原来,一个矩阵A乘以一个向量x,可以理解为,将A的所有列向量,以x各个项作为权重进行线性组合,所得向量即为乘得的结果。相应的,Ax = b这个方程也可以理解为求解一个矩阵A的列向量的线性组合,使得其等于b。
----
看到讲向量的表示一段,虽然一度对于向量的物理意义理解及其混乱(二维空间中的一个点还是一条没有位置只有方向和长度的线段),甚至为何(1,0)(0,1)被默认为单位向量且在坐标轴中垂直亦搞不懂其中玄机,不过这里倒是可以对向量相加的物理意义做一简单解释:由于向量可以理解为一个点到另一个点的移动,两个向量v、w相加可以理解为点先按v移动,接着按w移动。这也能解释为何两个方向不同的向量相加总小于方向相同的向量相加,因为前者相当于在沿着两个向量移动时走了些冤枉路,有些移动相互抵消了。
刚刚忽然想到,解析几何应该是严格建立在“正交”(垂直)概念的基础之上的(没去研究过讲几何学本质的著作哈,纯粹瞎扯),但“正交”这个概念在线代里真的颇有些蛋生鸡鸡生蛋的意味,玄机还没搞懂。
----
1.2给出了点乘的一个物理意义:假设两个物体在一个平衡杆上的位置分别为(v1,v2)(以平衡点为0),两个物体的重量分别为(w1,w2),则两个向量的点乘为力矩之和。力矩之和为0表示两物体平衡。另一个例子是一个向量表示单价,一个向量表示个数,点乘为总价。
----
1.3矩阵乘向量一节给出了两种认识这种运算的方法,这应该是线代里很重要的一个概念。
一个矩阵乘以一个(列)向量Ax,可以理解为:
- 矩阵A的所有列,以x的每个项为权重进行线性组合,即:
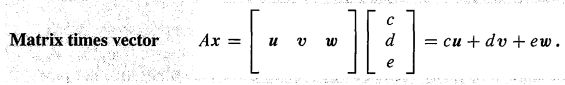
- 矩阵A的所有行与x做点乘,所得的每个结果作为结果向量的每一项,即:
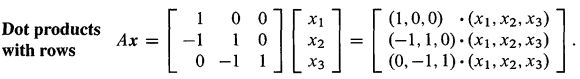
----
讲线代的书竟然讲起了微积分,而且还帮助我理解了之前看过的论文里的一个方法的数学背景:
1.3里进一步提到了如何求解离散数值的偏导,其中有三种方法:
后向差异:d(t)=x(t)-x(t-1)
前向差异:d(t)=x(t+1)-x(t)
中心差异:d(t)=(x(t+1)-x(t-1))/2
并以x(t)=t2为例提出中心差异貌似是对偏导更准确的一种近似。这也解释了之前看Marching Cubes那篇论文(有可能是图形学里最知名的一篇论文了)时作者所也使用类似方法来求梯度的原因。
----
鉴于作者一再强调row picture和column picture,这里就强调下:
row picture:一个矩阵方程Ax=b的解x,可以理解为每个线性方程所定义的平面(或超平面,其实二维空间里一条直线也是个一个“平面”哈)的相交点。当然这些平面可能不相交于一点,那应该就是相交于所在空间的子空间吧!!
column picture:一个矩阵方程Ax=b的解x,可以理解为找到A的列向量的一个线性组合,使得这个线性组合等于b。而这个线性组合的每个向量的系数即为x。
先说个有些跳跃的话题,由于先看过了SVD的章节,作者也是一再强调列空间和行空间,看来列于行之间纠结缠绕、你中有我的关系貌似真的是线性代数的真爱所在啊!!
----
看到将矩阵相乘一节,矩阵相乘,如果AB,可以理解为,B为一个源矩阵,A为一个描述转换的矩阵,AB所得矩阵即为对B按照A进行转换的结果。而转换的过程为:A的每一行描述了结果矩阵对应行的转换;A某行的每一列描述了这个列在B中对应行的系数,而最终结果矩阵的对应行则为B的每一行按照这个系数相加所得。
由于矩阵相乘A可以理解A对B进行一系列行操作所得,而高斯消元法就是有一系列的行操作组成,因此高斯消元的过程也可以表示为一系列的矩阵相乘。
----
之前说过,矩阵与向量相乘可以有两种理解方式,即矩阵每一行与向量点乘,与矩阵每一列以向量的项为系数进行线性组合。而两个矩阵AB相乘则有四种理解方式:
column picture: A乘以B等于A乘以B的每一列,所得每一个向量作为结果矩阵的每一列
row picture: A乘以B等于A的每一行乘以B,所得每一个行向量作为结果矩阵的每一行。其中A的某一行乘以B可以理解为对B做行变换
row column picture: A乘以B等于A的每一行与B的每一列做点乘,其中A的i行与B的j行相乘所得为结果矩阵C的Cij元素
column row picture: A乘以B等于A的第k列与B的第k行相乘所得的n个矩阵相加所得,其中n=A的列数=B的行数,则k取值为1到n
----
关于矩阵相乘时的分块矩阵相乘:
两矩阵AB相乘还可以理解为其各自分块矩阵的相乘。其中左矩阵A的行分割和右矩阵B的列分割可以任意,而A的列分割与B的行分割必须一致(注意这些分割不一定都是等分)。分割后的矩阵相乘结果有点类似矩阵相乘以元素为单位的解释方法:
即分块后A的第i行的矩阵与分块后B的第j列的矩阵做“点乘”,所得矩阵放到结果矩阵的第i行、第j列。
由于之前讲过,高斯消元可以通过对一个矩阵左乘一个“消元矩阵”(elimination matrix)来得到,但那里面讲的是一次只消去一行里相应的“枢轴”,如何一下子消去所有其他行的枢轴呢?有Schur Complement(抱歉不知道怎么翻译):
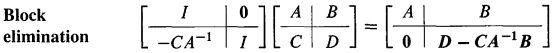
其中,消元矩阵里左下的块矩阵-CA-1颇为耐人寻味。看着是不是有点眼熟?是不是和消除单个元所用的-a/c异曲同工?
----
在谈到两矩阵AB相乘的逆等于B-1A-1时,作者指出:逆矩阵应以逆序做相乘,并给出一个很精辟的比喻:穿上袜子然后穿鞋的逆行为应是先脱下鞋然后脱下袜子。个人认为可以更加形式化的去理解:如果把每一个矩阵理解为一个变换或者映射(事实上矩阵确实也是做这个的哈),那么几个矩阵相乘可以理解为这几个变换的组合。这个组合的逆变换应该是先对最近一次变换取逆,然后是最近第二次的变换,然后是之前的变换。
V]8477(QJPVKERI_R9V]]0.png)