空间插值文献阅读(Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall)
空间插值技术应用必读论文---P. Goovaerts, Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. Journal of Hydrology, 2000, 113-129.
本博文从研究意义、研究区及预处理、所使用的插值方法以及对插值方法的评价这四个角度对该文进行了详细评述,并分析了该文的一些不足。
1内容评述
该文利用三种以高程作为辅助信息的克里金插值法来对降水量进行预测,分别为局部平均简单克里金法(simple kriging with locally varying mean, SKlm)、带有外部漂移的克里金法(kriging with external drift, KED)和同位协同克里金法(collocated cokriging, CC),然后利用交叉验证评价方法将上述三种方法得出的结果与传统的泰森多边形法、反距离平方加权法、普通克里金法以及线性回归法得到的结果进行比较。本章将从意义、研究区及预处理、所使用的插值方法以及评价方法这四个角度对该文进行详细描述。
1.1 文章的意义
对降雨量的空间分布进行预测很重要,目前出现了较多针对该问题的插值方法。传统的插值法,如泰森多边形法、反距离平方加权法、普通克里金法等只能利用各个站点降水量数据进行预测,当站点分布比较稀疏时,传统的方法不能很好的进行预测。
我们知道,降水量与高程存在较强的正相关关系,高的地方(如山区)降水量一般都比较大。一些地统计方法如SKlm、KED和CC不仅能利用较稀疏的各个站点的降水量数据(主数据),还能利用易得的辅助数据(辅助数据需与主数据有较强的相关性),比如数字高程模型(DEM,是规则格网,每个格网的数据代表了该点的高度),对降水量数据进行插值。该文使用这两类不同的方法(一类只使用水文站点的降水量数据,一类除使用降水量数据外还使用了高程数据)来对降水量的空间分布进行预测,并进行了评价。
1.2 研究区及预处理
研究区为Algarve地区,面积5000km2。数据为1970年-1995年36个站点的月平均和年平均水量数据以及该地区的DEM数据,DEM分辨率为1km2。对这些数据的预处理的步骤如下:
首先分析降水量和高程的相关性。降水量与高程的皮尔森相关系数为0.33-0.83,除去7月和8月这两个枯水季,降水量与高程皮尔森相关系数为0.50-0.97,可见降水量与高程之间有明显的相关性。
然后对站点的降水量数据进行半方差分析。由于数据较少,该文不考虑方向性问题。由数据得到半方差图,发现半方差图在lag为25km时达到最高,然后突然降低并呈现波动震荡趋势,该文把此现象称为“hole effect”(孔洞效应)。该现象反映了原始数据有周期性重复现象,该文将此现象归因于研究区中的两座高山,因为高山的降水量较大。
最后对半方差图进行拟合。该文使用回归方法对以下三个理论模型进行了拟合。
球面模型(Spherical model):  (1)
(1)
立方模型(Cubic model): 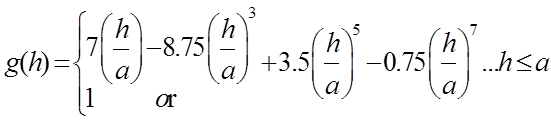 (2)
(2)
孔洞效应模型(Dampened hole effect model): ![]() (3)
(3)
如何判定上述三个理论模型的拟合效果呢?该文使用的判断依据是WSS(weighted sum of squares,实验变差函数与理论模型值之差的加权和)最小这一指标。
 (4)
(4)
![]() (5)
(5)
比较上述三个模型的WSS,发现立方模型(Cubic model)的WSS最小,所以该文选择的理论半方差模型为立方模型(Cubic model)。
1.3 插值方法
在对数据进行了详细分析及预处理后,就可对降水量进行插值。对降水量数据进行插值的方法很多,根据是否使用辅助数据分成两类。本小节对这两类方法进行评述。
1.3.1 传统的方法
1) 泰森多边形法:首先找到与该待插值点在空间上最近的一个站点,将站点的降水量数据赋予该点即可。该法优点是简单,缺点是形成斑块,结果不真实。
2) 反距离平方加权法:待插值点的值是该点附近已知站点数据的线性组合,线性组合的权重为该点与附近站点欧式距离平方的反比。该法基于这样一个假设:与待插值点越近的测量点,其数据与待插点的真值也越接近。该法优点是结果较为平缓,不形成斑块,缺点是不能保证估计方差最小。
3) 普通克里金法:与反距离平方加权法相似,只是线性组合的权重需要求解方程组得到。
该法的步骤为:使用预处理中给出的理论半方差模型,通过无偏和估计方差最小这两个条件来联列方程组求解权重系数。该法的优点是能使估计误差最小,缺点是当观测点数据较少时,得到的结果不可靠。
1.3.2. 结合高程信息(辅助数据)的方法
1) 线性回归法:因为降水量数据与高程数据相关性较强,可以直接构造线性回归方程(当主数据与辅助数据不是线性相关时,可以转换辅助数据使之线性相关),然后对空间上每一点进行求值。该法的优点是直观简单,缺点是认为线性回归后的残差空间不相关,而通过对残差数据进行分析发现是空间相关的。
![]() (6)
(6)
2) SKlm法:SKlm法首先通过主辅数据间的相互关系来求得线性关系式,该关系式利用整体数据只求一次,用于整个区域的估值;然后对残差进行简单克里金,如果残差不相关,那么所有克里金的权重系数为0,插值结果就是线性回归得到的结果。该法的优点是考虑了残差的空间相关性,线性回归可以看作其一个特例(残差空间不相关)。
 (7)
(7)
 (8)
(8)
3) KED法:KED利用处处已知的辅助变量,并且假设辅助变量能够反映主变量的局部空间趋势,与SKlm相似,不同之处在于对局部平均值的求解。对于SKlm法,利用所有测量点求解一次线性关系式,用于整个区域的估值,而KED法则在每个搜索邻域内进行估计,即KED的主辅数据之间的关系是局部估计的。KED使用局部邻域估计主辅数据之间的线性函数关系,比SKlm利用所有主辅数据之间的关系更合理。
 (9)
(9)
 (10)
(10)
4) CC法:是协同克里金法的一种简化形式,即如果辅助变量密集取样的时候,只保留与待插值点同位的辅助数据。CC法与SKlm法和KED法不同,SKlm法和KED法是间接的利用高程的信息,即利用高程信息得到趋势值,而CC法则是直接将高程数据应用到估值中。
![]() (11)
(11)
1.3.3 对各插值方法的评价
使用交叉验证的方法。交叉验证法是依次假设每个实测数据点均未被测定,根据n-1个其它测定点的数据用某种插值方法来估计这个假设未被测定的值(假设共有n个实测数据)。结果发现泰森多边形法和反距离平方加权法的得到的结果误差最大,因为这两种方法同时忽略了高程信息和周围站点测的降水量的信息。SKlm法、KED法和CC法较其它方法得到的结果更为精确。而当高程与降水量的相关性不是很强的时候(在本研究中皮尔森相关系数小于0.75时),普通克里金法得到的结果比线性回归法好。
2 文章带来的启发
通过对该文献的阅读和理解,加深了对克里金插值方法的认识,对克里金插值的流程有了进一步的熟悉,最重要的一点收获是,在对数据进行插值时,如果主数据和辅助数据存在较好的相关性,我们不仅可以对主数据进行直接插值,还能结合辅助数据进行插值。
3 文章研究的不足
虽然该文逻辑清晰,方法多样,对结果的意义解释也很明了,但对该文进行仔细分析,仍可发现存在如下几点不足:
1) 选取普通克里金法作为传统方法的一种并不合适。该文为了体现结合高程信息插值方法的优势,选取了三种只使用降水量数据的传统方法作为对比,其中有普通克里金方法,但我认为选择普通克里金方法是不合适的,泛克里金方法比较合适。我们知道,普通克里金方法是基于均值在随机场上不变的思想,而在该文研究中,降水量是随着地形的变化而变化的,在高山地区的降水量均值明显较大,也就是说其均值是随着位置的改变而改变的,因此使用普通克里金方法来进行插值不合适,故而可以考虑使用趋势面法或者泛克里金方法。
2) 该文建立了降水量与高程的线性回归模型,并认为该回归的不足是没有考虑残差的线性相关性,从而引发了使用各种克里金方法。基于此,可以考虑使用GLMs方法来对降水量进行预测。
3) 该文认为数据量比较小,不考虑数据的有向性问题,但该数据可能存在有向性,因为受高程影响,数据分布与高程也一致,而由于山脉的有向分布可能导致数据存在有向性。可以考虑使用周期图进行分析,这样不管原始数据有向还是无向都可以进行分析。
4) 该文对年平均降水量和月平均降水量进行了空间分布的预测,是否可以按季节进行分类,对季平均降水量进行空间分布的预测?
5) 是否考虑使用时空模型,来对不同空间和不同时间的降水量进行预测?